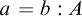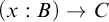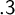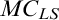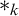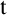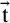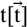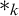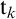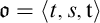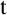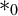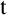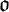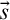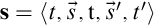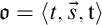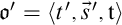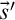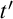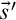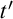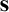Gazzari provides a mathematical theory of occurrences and of substitutions, which are a generalisation of occurrences constituting substitution functions. The dissertation focusses on term occurrences in terms of a first order language, but the methods and results obtained there can easily be carried over to arbitrary kinds of occurrences in arbitrary kinds of languages.
The aim of the dissertation is twofold: first, Gazzari intends to provide an adequate formal representation of philosophically relevant concepts (not only of occurrences and substitutions, but also of substitution functions, of calculations as well as of intuitively given properties of the discussed entities) and to improve this way our understanding of these concepts; second, he intends to provide a formal exploration of the introduced concepts including the detailed development of the methods needed for their adequate treatment.
The dissertation serves as a methodological fundament for consecutive research on topics demanding a precise treatment of occurrences and as a foundation for all scientific work dealing with occurrences only informally; the formal investigations are complemented by a brief survey of the development of the notion of occurrences in mathematics, philosophy and computer science.
The notion of occurrences. Occurrences are determined by three aspects: an occurrence is always an occurrence of a syntactic entity (its shape) in a syntactic entity (its context) at a specific position. Context and shape can be any meaningful combination of well-known syntactic entities as, in logic, terms, formulae or formula trees. Gazzari’s crucial idea is to represent the position of occurrences by nominal forms, essentially as introduced by Schütte [2]. The nominal forms are a generalisation of standard syntactic entities in which so called nominal symbols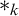 $*_k$
may occur. The position of an occurrence is obtained by eliminating the intended shape in the context, which means to replace the intended shape by suitable nominal symbols.
$*_k$
may occur. The position of an occurrence is obtained by eliminating the intended shape in the context, which means to replace the intended shape by suitable nominal symbols.
Standard occurrences. Central tool of the theory of nominal terms (nominal forms generalising standard terms) is the general substitution function mapping a nominal term 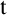 $\mathtt {t}$
and a sequence
$\mathtt {t}$
and a sequence 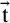 $\vec {\mathtt {t}}$
of them to the result
$\vec {\mathtt {t}}$
of them to the result 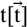 $\mathtt {t}[\vec {\mathtt {t}}]$
of replacing simultaneously the nominal symbols
$\mathtt {t}[\vec {\mathtt {t}}]$
of replacing simultaneously the nominal symbols 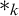 $*_k$
in the first argument by the respective entries
$*_k$
in the first argument by the respective entries 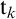 $\mathtt {t}_k$
of the second argument.
$\mathtt {t}_k$
of the second argument.
A triple 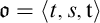 $\mathfrak {o}=\langle {t,s,\mathtt {t}} \rangle $
is a standard occurrence, if an application of the general substitution function on the position
$\mathfrak {o}=\langle {t,s,\mathtt {t}} \rangle $
is a standard occurrence, if an application of the general substitution function on the position 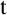 $\mathtt {t}$
and the shape s results in the context t of that occurrence. As
$\mathtt {t}$
and the shape s results in the context t of that occurrence. As 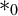 $*_0$
can occur more than once in
$*_0$
can occur more than once in 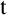 $\mathtt {t}$
, arbitrary many single occurrences in the context t of the common shape s can be subsumed in
$\mathtt {t}$
, arbitrary many single occurrences in the context t of the common shape s can be subsumed in 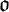 $\mathfrak {o}$
.1 Gazzari illustrates the appropriateness of his approach by solving typical problems (counting formally the number of specific occurrences, deciding whether an occurrence lies within another) which are not solvable without a good theory of occurrences.
$\mathfrak {o}$
.1 Gazzari illustrates the appropriateness of his approach by solving typical problems (counting formally the number of specific occurrences, deciding whether an occurrence lies within another) which are not solvable without a good theory of occurrences.
Multi-shape occurrences. The multi-shape occurrences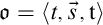 $\mathfrak {o}=\langle {t,\vec s,\mathtt {t}} \rangle $
are the generalisation of standard occurrences, where the shape
$\mathfrak {o}=\langle {t,\vec s,\mathtt {t}} \rangle $
are the generalisation of standard occurrences, where the shape 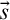 $\vec s$
is a sequence of standard terms. Such occurrences subsume arbitrary non-overlapping single occurrences in the context t.
$\vec s$
is a sequence of standard terms. Such occurrences subsume arbitrary non-overlapping single occurrences in the context t.
Gazzari addresses the non-trivial identity of such occurrences and their independence. The latter represents formally the idea of non-overlapping occurrences and is a far-reaching generalisation of disjointness as discussed by Huet with respect to single occurrences. Independent occurrences can be merged into one occurrence; an occurrence can be split up into independent occurrences.
Substitutions. A substitution 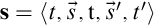 $\mathbf s=\langle {t,\vec s,\mathtt {t},{\vec s}',t'} \rangle $
satisfies that both
$\mathbf s=\langle {t,\vec s,\mathtt {t},{\vec s}',t'} \rangle $
satisfies that both 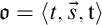 $\mathfrak {o}=\langle {t,\vec s,\mathtt {t}} \rangle $
and
$\mathfrak {o}=\langle {t,\vec s,\mathtt {t}} \rangle $
and 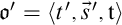 $\mathfrak {o}'=\langle {t',{\vec s}',\mathtt {t}} \rangle $
are occurrences such that the shapes have the same length. Such a substitution represents the replacement of
$\mathfrak {o}'=\langle {t',{\vec s}',\mathtt {t}} \rangle $
are occurrences such that the shapes have the same length. Such a substitution represents the replacement of 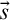 $\vec s$
in t at
$\vec s$
in t at 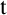 $\mathtt {t}$
by
$\mathtt {t}$
by 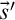 $\vec s'$
resulting in
$\vec s'$
resulting in 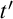 $t'$
. This means that a substitution is understood as a process and not as a (specific type of a) function.
$t'$
. This means that a substitution is understood as a process and not as a (specific type of a) function.
Identity and independence are addressed again, using and extending the methods developed for occurrences; as before, independent substitutions can be merged and substitutions can be split up into sequences of independent substitutions. Substitutions are used to represent formally calculations (as found in everyday mathematics) and to investigate them.
Sets of substitutions turn out to be set-theoretic functions mapping the affected occurrences 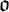 $\mathfrak {o}$
and the inserted shapes
$\mathfrak {o}$
and the inserted shapes 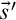 ${\vec s}'$
to the result
${\vec s}'$
to the result 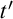 $t'$
of a substitution
$t'$
of a substitution 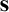 $\mathbf s$
. Such sets are called explicit substitution functions. In order to qualify functions which are usually understood as substitution functions (and which are not formulated in a theory of occurrences) as substitution functions, Gazzari develops the concept of an explication method transforming such functions into explicit substitution functions. The appropriateness and the (philosophical) limitations of this concept are illustrated with example functions.
$\mathbf s$
. Such sets are called explicit substitution functions. In order to qualify functions which are usually understood as substitution functions (and which are not formulated in a theory of occurrences) as substitution functions, Gazzari develops the concept of an explication method transforming such functions into explicit substitution functions. The appropriateness and the (philosophical) limitations of this concept are illustrated with example functions.
Conclusion. Gazzari’s theory of occurrences is strong (not restricted to single occurrences), canonical (nominal forms are a canonical generalisation of the underlying syntactic entities) and general (presupposing the grammar for the underlying syntactic entities, suitable nominal forms are easily defined and the theory of occurrences is immediately carried over). Another advantage is a kind of methodological pureness: positions are generalised syntactic entities (and not extraneous, as sequences of natural numbers) and can be treated, in particular, with the well-known methods developed for the underlying syntactic entities.
Abstract prepared by René Gazzari.
E-mail: rene.gazzari@uni-tuebingen.de
URL: http://doi.org/10.15496/publikation-47553
 $\Gamma _{0}$
$\Gamma _{0}$