Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T11:35:47.270Z Has data issue: false hasContentIssue false
  • English
  • Français

A CLASSICAL MODAL THEORY OF LAWLESS SEQUENCES

Part of: Philosophical aspects of logic and foundations General and miscellaneous specific topics Proof theory and constructive mathematics

Published online by Cambridge University Press:  09 March 2023

ETHAN BRAUER Open the ORCID record for ETHAN BRAUER [Opens in a new window]
ETHAN BRAUER*
Affiliation:
DEPARTMENT OF PHILOSOPHY LINGNAN UNIVERSITY 8 CASTLE PEAK RD. TUEN MUN, HONG KONG E-mail: eebrauer@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Free choice sequences play a key role in the intuitionistic theory of the continuum and especially in the theorems of intuitionistic analysis that conflict with classical analysis, leading many classical mathematicians to reject the concept of a free choice sequence. By treating free choice sequences as potentially infinite objects, however, they can be comfortably situated alongside classical analysis, allowing a rapprochement of these two mathematical traditions. Building on recent work on the modal analysis of potential infinity, I formulate a modal theory of the free choice sequences known as lawless sequences. Intrinsically well-motivated axioms for lawless sequences are added to a background theory of classical second-order arithmetic, leading to a theory I call 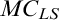$MC_{LS}$. This theory interprets the standard intuitionistic theory of lawless sequences and is conservative over the classical background theory.

Keywords

Brouwerintuitionismintuitionistic analysisfree choice sequencespotentialismpotential infinity

MSC classification

Primary: 03F25: Relative consistency and interpretations 03F50: Metamathematics of constructive systems 03F55: Intuitionistic mathematics
Secondary: 00A30: Philosophy of mathematics 03A05: Philosophical and critical
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 29 , Issue 3 , September 2023 , pp. 406 - 452
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

van Atten, M., Brouwer Meets Husserl: On the Phenomenology of Choice Sequences , Springer, Dordrecht, 2007.CrossRefGoogle Scholar
van Atten, M., The creating subject, the Brouwer–Kripke schema, and infinite proofs . Indagationes Mathematicae , vol. 29 (2018), no. 6, pp. 1565–1636.CrossRefGoogle Scholar
van Atten, M. and van Dalen, D., Arguments for the continuity principle, this Journal, vol. 8 (2002), no. 3, pp. 329–347.Google Scholar
Bishop, E., Foundations of Constructive Analysis , McGraw-Hill, New York, 1967.Google Scholar
Boolos, G., The Logic of Provability , Cambridge University Press, Cambridge, 1993.Google Scholar
Brauer, E., The modal logic of potential infinity: Branching vs. convergent possibilities . Erkenntnis , vol. 87 (2020), pp. 2161–2179.CrossRefGoogle Scholar
Brauer, E., Linnebo, Ø., and Shapiro, S., Divergent Potentialism: A modal analysis with an application to choice sequences . Philosophia Mathematica , vol. 30 (2022), no. 2, pp. 143–172.CrossRefGoogle Scholar
Brouwer, L. E. J., A. Schoenflies und H. Hahn. Die Entwickelung der Mengenlehre und ihrer Anwendungen, Leipzig und Berlin 1913 . Jahresbericht der Deutschen Mathematiker-Vereinigung , vol. 23 (1914), pp. 78–83.Google Scholar
Brouwer, L. E. J., Historical background, principles and methods of intuitionism . South African Journal of Science , vol. 49 (1952), pp. 139–146.Google Scholar
Burgess, J. P., Decidability of branching time . Studia Logica , vol. 32 (1980), nos. 2–3, pp. 203–218.CrossRefGoogle Scholar
Dummett, M., Elements of Intuitionism , second ed., Oxford University Press, Oxford, 2000.Google Scholar
Emerson, E. A., Temporal and modal logics , Handbook of Theoretical Computer Science , vol. B (J. van Leeuwen, editor), MIT Press, Cambridge, MA, 1990, pp. 995–1072.Google Scholar
Feferman, S., Infinity in mathematics: Is Cantor necessary? , In the Light of Logic , Oxford University Press, New York, 1998.Google Scholar
Goodman, N., Epistemic arithmetic is a conservative extension of intuitionistic arithmetic . Journal of Symbolic Logic , vol. 49 (1984), no. 1, pp. 192–203.CrossRefGoogle Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic , Springer, Berlin, 1993.CrossRefGoogle Scholar
Hellman, G., Never say ‘never’!: On the communication problem between intuitionism and classicism . Philosophical Topics , vol. 17 (1989), no. 2, pp. 47–67.CrossRefGoogle Scholar
Heyting, A., Intuitionism , third ed., North Holland, Amsterdam, 1971.Google Scholar
Heyting, A., Intuitionistic views on the nature of mathematics . Synthese , vol. 21 (1974), pp. 79–91.CrossRefGoogle Scholar
Hughes, G. E. and Cresswell, M. J., A New Introduction to Modal Logic , Routledge, New York, 1996.CrossRefGoogle Scholar
Kripke, S., Free choice sequences: A temporal interpretation compatible with the acceptance of classical mathematics . Indagationes Mathematicae , vol. 30 (2019), no. 3, pp. 492–499.CrossRefGoogle Scholar
McCall, S., The strong future tense . Notre Dame Journal of Formal Logic , vol. 20 (1979), no. 3, pp. 489–504.CrossRefGoogle Scholar
McCarty, C., Proofs and constructions . Foundational Theories of Classical and Constructive Mathematics (G. Sommaruga, editor), Springer, New York, 2011, pp. 209–226.CrossRefGoogle Scholar
Moschovakis, J. R., A classical view of the intuitionistic continuum . Annals of Pure and Applied Logic , vol. 81 (1996), pp. 9–24.CrossRefGoogle Scholar
Moschovakis, J. R., Iterated definibility, lawless sequences, and Brouwer’s continuum , Gödel’s Disjunction (L. Horsten and P. Welch, editors), Oxford University Press, Oxford, 2016, pp. 92–107.CrossRefGoogle Scholar
Moschovakis, J. R., Intuitionistic analysis at the end of time, this Journal, vol. 23 (2017), no. 3, pp. 279–295.2017 Google Scholar
Myhill, J., Notes towards a formalization of intuitionistic analysis . Logique et Analyse , vol. 35 (1967), pp. 280–297.Google Scholar
Placek, T., Mathematical Intuitionism and Intersubjectivity , Kluwer, Dordrecht, 1999.CrossRefGoogle Scholar
Shapiro, S., Epistemic and intuitionistic arithmetic , Intensional Mathematics (S. Shapiro, editor), North Holland, Amsterdam, 1985, pp. 11–46.CrossRefGoogle Scholar
Tait, W., The Provenance of Pure Reason , Oxford University Press, New York, 2005.Google Scholar
Troelstra, A., The theory of choice sequences , Logic, Methodology, and Philosophy of Science III (B. Van Rootselaar and J. F. Staal, editors), North Holland, Amsterdam, 1968, pp. 201–223.CrossRefGoogle Scholar
Troelstra, A., Choice Sequences: A Chapter of Intuitionistic Mathematics , Clarendon Press, Oxford, 1977.Google Scholar
Troelstra, A., On the origin and development of Brouwer’s concept of choice sequence , L.E.J. Brouwer Centenary Symposium (A. Troelstra and D. van Dalen, editors), North Holland, Amsterdam, 1982, pp. 465–486.Google Scholar
Troelstra, A., Analyzing choice sequences . Journal of Philosophical Logic , vol. 12 (1983), no. 2, pp. 197–260.CrossRefGoogle Scholar
Troelstra, A. and van Dalen, D., Constructivism in Mathematics , 2 vols , North Holland, Amsterdam, 1988.Google Scholar