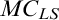1 Introduction
In developing intuitionistic mathematics, L.E.J. Brouwer introduced the notion of a free choice sequence. Roughly, these are potentially infinite sequences of natural numbers whose values are freely chosen sequentially, one by one. Free choice sequences are a central piece in the development of the intuitionistic theory of the continuum, being key to Brouwer’s continuity theorem, Brouwerian counterexamples to the law of excluded middle, and other characteristically intuitionistic theorems.Footnote 1
Free choice sequences are also among the more controversial aspects of Brouwerian intuitionism, and it is not hard to see why. The very conception of freely choosing the values of a sequence one after the other introduces agent-centric and temporal dimensions to mathematics that are foreign to traditional ways of thinking about mathematics. The fact that free choice sequences also lead to results that seemingly contradict classical mathematics makes them doubly suspect. In this respect the use of choice sequences in intuitionistic analysis differs from intuitionistic arithmetic. The intuitionistic theory of Heyting Arithmetic (HA) is a proper subtheory of classical Peano Arithmetic (PA), so the classical mathematician can regard HA as simply being the constructive fragment of PA.Footnote 2
Free choice sequences are thus often seen as, at best, the awkward stepchild left by Brouwerian intuitionism.Footnote 3 For instance, in an often-quoted passage, Bishop writes:
[Brouwer] seems to have [had] a nagging suspicion that unless he personally intervened to prevent it the continuum would turn out to be discrete. He therefore introduced the method of free-choice sequences for constructing the continuum, as a consequence of which the continuum cannot be discrete because it is not well enough defined. This makes mathematics so bizarre it becomes unpalatable to mathematicians, and foredooms the whole of Brouwer’s program. [Reference Bishop4, p. 6]
Feferman also comments (albeit somewhat less pessimistically):
Brouwer introduced … a novel conception, that of free choice sequences (f.c.s), … of which one would have only finite partial information at any stage. Then with the real numbers viewed as convergent f.c.s. of rationals, a function f from
![]() $\mathbb {R}$
to
$\mathbb {R}$
to
![]() $\mathbb {R}$
can be determined using only a finite amount of such information at any given argument. Brouwer used this line of reasoning to conclude that any function from
$\mathbb {R}$
can be determined using only a finite amount of such information at any given argument. Brouwer used this line of reasoning to conclude that any function from
![]() $\mathbb {R}$
to
$\mathbb {R}$
to
![]() $\mathbb {R}$
must be continuous, in direct contradiction to the classical existence of discontinuous functions. With this step Brouwer struck off into increasingly alien territory, and he found few to follow him even among those sympathetic to the constructive position. [Reference Feferman13, p. 47]
$\mathbb {R}$
must be continuous, in direct contradiction to the classical existence of discontinuous functions. With this step Brouwer struck off into increasingly alien territory, and he found few to follow him even among those sympathetic to the constructive position. [Reference Feferman13, p. 47]
And Tait writes:
I am … rejecting the Brouwerian conception that the subject has individuated an infinite choice sequence by the act of beginning to choose its successive members. For this idea depends upon a subjectivist stance: the sequence in question is the one that I am choosing; it is always unfinished but becomes more determinate in time, as I make more and more choices. … From an objectivist point of view, time does not enter into mathematics: its truths are time independent. [Reference Tait29, p. 16]
We can discern at least three different objections to free choice sequences: they introduce a temporal aspect to mathematics, they introduce a subjective or agential aspect to mathematics, and they lead to results that, at least apparently, contradict classical mathematics.Footnote 4 Together, these objections can foster a suspicion that the concept of choice sequences as mathematical objects is deeply bizarre, if not incomprehensible. I aim to dispel this suspicion.
This paper is the first step in a project of developing a modal theory of free choice sequences in a classical background theory. An upshot of this project will be that each of the three objections to free choice sequences is either erroneous or ultimately unproblematic. The objection that free choice sequences introduce a temporal dimension into mathematics will be defused. My account does take the temporal nature of free choice sequences seriously, giving it an explicit treatment using the resources of modal logic. Modal logic is a well-understood and mathematically sensible framework, and its use in a theory of free choice sequences should be no more problematic than in, say, logics of program verification or of provability.Footnote 5 The result is a perfectly sensible mathematical theory of intratemporal objects, and the truths of this theory are as objective and time-independent as those in any other area of mathematics—just as Tait would have it.
The objection that free choice sequences introduce a subjective or agential aspect to mathematics is shown to be simply erroneous. Nowhere does the notion of an agent or a subject actually appear in my theory. The notion of a mathematical agent is a useful heuristic and helps motivate certain choices of axioms, but this is entirely at the pre-formal level.
Finally, the objection that free choice sequences lead to results that contradict classical mathematics is also shown to be erroneous, since my theory explicitly includes standard second-order arithmetic alongside free choice sequences, and all with classical logic in the background. The modal theory of free choice sequences will ultimately suffice to prove theorems analogous to many of the intuitionists’ famous anti-classical results. In the modal setting, however, these theorems concern the intratemporal free choice sequences, and hence are modal in character, rather than concerning the familiar classical real numbers. As such, my project could reasonably be described as following the reinterpretation strategy alluded to in footnote 4. On the other hand, the intuitive motivation is sufficiently clear and its formalization sufficiently natural that calling my theory a reinterpretation of intuitionistic discourse is not entirely satisfactory. It might be better described as a modal implementation of intuitionistic ideas.
1.1 The goal
The goal of the overarching project is to analyze choice sequences in modal terms in a classical background theory. There are two things that I hope to accomplish with this project: first, to show that the notion of free choice sequence is comprehensible from the classical point of view, and, second, to show how, having done so, portions of intuitionistic analysis (or rather, modal analogues thereof) are available to the classical point of view. To the extent that this second goal is accomplished, classical and intuitionistic mathematics need not be seen as competing or alternative approaches to math, and intuitionistic mathematics—in particular, portions of intuitionistic analysis—can be seen to be legitimate from the classical perspective.
In this paper specifically, I will develop a modal theory of so-called lawless sequences and show that it interprets the intuitionistic theory of lawless sequences. The intuitionistic theory of lawless sequences is a nice place to begin because it is well-understood and relatively simple, and also because it provides a starting point for defining more complex theories of choice sequences. In future work I plan to extend this theory to include non-lawless sequences that suffice for a theory of real numbers.
This project can be seen in part as following up on a recent proposal from [Reference Kripke20]. There, Kripke “outline[s] how a concept of free choice sequence could be combined with an acceptance of classical mathematics” (p. 3). The essential idea is to imagine a classical mathematician facing a potential infinity of points in time at which they can freely choose values for a growing sequence of natural numbers. Kripke’s paper is largely programmatic, though; he does not present any explicit theory of temporal free choice sequences that is meant to extend classical analysis and only briefly discusses which intuitionistic principles might carry over to the setting he proposes. My aim is to address exactly such questions, moving beyond informal conceptions or intuitive motivations to give an explicit and properly mathematical theory of free choice sequences.
Moschovakis [Reference Moschovakis25] has also introduced a system inspired by Kripke’s proposal. Her approach is to use a multi-sorted theory that contains intuitionistic analysis, a negative translation of classical analysis, and an axiom asserting that for any choice sequence it is not impossible that there is a determinate (lawlike) sequence that agrees everywhere with it. A realizability argument shows the theory to be consistent.Footnote 6 Perhaps the most important difference between Moschovakis’ system and the approach below is that I take the temporal aspect of choice sequences to be an integral part of the concept; accordingly, the temporal aspect figures explicitly in my theory in the form of modal operators. As Moschovakis observes in the conclusion of her article, her theory “gives no further insight into the stage-by-stage activity of a creating subject. All we can claim is that from the perspective (unattainable by the creating subject) of the end of time, Kripke’s idea is classically feasible” [25, p. 294]. In this paper, by contrast, I will give the step-by-step activity of the idealized mathematician a central role in motivating our choice of axioms, and the step-by-step manner in which lawless sequences get defined is directly mirrored in the modal nature of the theory.
1.2 Outline of the paper and main results
There are two main results of this paper. First, I show that my modal theory of lawless sequences
![]() $MC_{LS}$
interprets the intuitionistic theory of lawless sequences
$MC_{LS}$
interprets the intuitionistic theory of lawless sequences
![]() $LS$
(Theorem 8.21). Second, I show that whenever Z is a subsystem of second-order arithmetic extending
$LS$
(Theorem 8.21). Second, I show that whenever Z is a subsystem of second-order arithmetic extending
![]() $RCA_0$
, if
$RCA_0$
, if
![]() $MC_{LS}(Z)$
is just like
$MC_{LS}(Z)$
is just like
![]() $MC_{LS}$
but with the induction and comprehension axioms restricted as they are in Z, then
$MC_{LS}$
but with the induction and comprehension axioms restricted as they are in Z, then
![]() $MC_{LS}(Z)$
is conservative over Z (Corollary 9.8).
$MC_{LS}(Z)$
is conservative over Z (Corollary 9.8).
In Sections 2–5 I will introduce my theory of lawless sequences. Section 2 provides the background on Brouwer’s conception of lawless sequences. Section 3 introduces some notational conventions I adopt. Section 4 describes the modal logic my theory is based on. And Section 5 then formally introduces the theory of lawless sequences.
Sections 6–8 cover the interpretation of the intuitionistic theory of lawless sequences
![]() $LS$
. Section 6 presents the intuitionistic theory
$LS$
. Section 6 presents the intuitionistic theory
![]() $LS$
. Section 7 describes the translation I use. In Section 8, I prove the interpretation result.
$LS$
. Section 7 describes the translation I use. In Section 8, I prove the interpretation result.
Finally, in Section 9 I discuss the relation between
![]() $MC_{LS}$
and classical second-order arithmetic. I give a model-theoretic conservation argument showing how any model of a subsystem Z of second-order arithmetic can be used to create a model for
$MC_{LS}$
and classical second-order arithmetic. I give a model-theoretic conservation argument showing how any model of a subsystem Z of second-order arithmetic can be used to create a model for
![]() $MC_{LS}(Z)$
.
$MC_{LS}(Z)$
.
2 Free choice sequences
The basic idea of a choice sequence can be seen as arising from two components of Brouwer’s thought. The first component was his metaphysical views: Brouwer, of course, thought of mathematical objects as purely mental constructions with no objective or mind-independent existence. Accordingly, one could not truly assert the existence of some mathematical object without a method for constructing that object mentally.
The second component of Brouwer’s thought was his acceptance of the arithmetized account of the continuum that had become widespread in classical mathematics since Dedekind and Cantor.Footnote 7 The arithmetized view of the continuum required defining real numbers in terms of infinite sets or sequences of rational numbers (à la Dedekind cuts, Cauchy sequences, or infinite decimal expansions). Brouwer’s constructivism required that any such sets or sequences must be given as possible mental constructions. For simplicity I will simply talk of sequences rather than sequences or sets. If there is a law that can be followed to construct the sequence, such a sequence passes constructivist muster, since the law provides a method for constructing the sequence. But the fullness of the continuum is not exhausted by (to fix ideas) the Cauchy sequences that can be given by a law. One wants to countenance any arbitrary Cauchy sequences. And the idea of an arbitrary Cauchy sequences emerges in intuitionism as a free choice sequence: an infinitely proceeding series of choices of rational numbers determined freely by an agent.
Since mathematical agents are limited, we must regard these sequences as necessarily unfinished. But the intuitionist regards objects that could, at least in principle, be constructed by a mathematician as legitimate objects of study. And since there is no in-principle finite limit to how long of a sequence a mathematician could create, we can regard a choice sequence as indefinitely proceeding, though not as a completed infinite sequence.
Because of this idealization involved, it is common to describe choice sequences as potentially infinite sequences of numbers created by an idealized mathematician subsequently picking each member of the sequence. They are free to pick any number they like; but they are also free to impose constraints on their future choices. Thus we countenance choice sequences that are, after some stage, bound by some laws as well as those that are free from all constraints.
As Brouwer [Reference Brouwer9, p. 140] described the matter:
[Intuitionism] recognizes the possibility of generating new mathematical entities: firstly in the form of infinitely proceeding sequences
![]() $p_1,p_2,\dots $
, whose terms are chosen more or less freely from mathematical entities previously acquired; in such a way that the freedom of choice existing perhaps for the first element
$p_1,p_2,\dots $
, whose terms are chosen more or less freely from mathematical entities previously acquired; in such a way that the freedom of choice existing perhaps for the first element
![]() $p_1$
may be subjected to a lasting restriction at some following
$p_1$
may be subjected to a lasting restriction at some following
![]() $p_v$
, and again and again to sharper lasting restrictions or even abolition at further subsequent
$p_v$
, and again and again to sharper lasting restrictions or even abolition at further subsequent
![]() $p_v$
’s, while all these restricting interventions, as well as the choices of the
$p_v$
’s, while all these restricting interventions, as well as the choices of the
![]() $p_v$
’s themselves, at any stage may be made to depend on possible future mathematical experiences of the creating subject.
$p_v$
’s themselves, at any stage may be made to depend on possible future mathematical experiences of the creating subject.
Brouwer here countenances a wide range of choice sequences that includes sequences of any type of mathematical object that is already available. Most subsequent studies of choice sequences have, however, only considered sequences of natural numbers, and I will do likewise in this project. Lawless sequences are a specific type of free choice sequence wherein the creating mathematician determines from the beginning that they shall never subject their choices to any restriction or law. The choice of each value for the sequence is entirely unconstrained and subject to no law.
These ideas of Brouwer’s express the basic concept of a free choice sequence which I will be trying to capture in a modal framework. At the same time, in giving the modal account I do not take myself to necessarily be bound by any particular statement or idea of Brouwer’s. Given that his own ideas about choice sequences changed a number of times over his lifetime, this is not a feasible or even desirable goal.Footnote 8 Similarly, a variety of explicit accounts of choice sequences developed in later intuitionistic literature, and while they all share some central features, they also differ in important respects. This situation led Troelstra to claim in a survey article that “there are a great many notions of choice sequence which have to be regarded as distinct primitive notions” ([Reference Troelstra33, p. 225], emphasis original). This should not be taken to suggest that there is no core intuitive notion of a free choice sequence—in this section I have sketched just such a notion. Troelstra’s point, rather, is that in fleshing out a fully detailed account of choice sequences there are a number of decision points where multiple ways of proceeding are compatible with the core idea of a free choice sequence. (These decision points, however, concern free choice sequences that lie beyond the realm of lawless sequences. Lawless sequences themselves form a shared basis on which different more complicated conceptions of choice sequences can agree. This is a further reason for focusing on lawless sequences in this paper.)
Although this situation precludes a simple appeal to a generally accepted definition of a choice sequence, we can still take it as an ideal for the modal account of choice sequence to cohere with the conception(s) of choice sequence found in Brouwer, Heyting, Troelstra, and other intuitionists. The important thing is that the modal account should allow us to capture the role that choice sequences play in intuitionistic arguments. I aim to make good on this by showing how a modal theory of choice sequences allows us to prove modal analogues of important intuitionistic results.
I turn now from this informal introduction to the idea of a free choice sequence to consider specific formal theories of lawless sequences.
3 Notational preliminaries
I will use a sort of variables for choice sequences
![]() $\alpha , \beta , \gamma ,\dots $
; intuitively these will be partial functions on
$\alpha , \beta , \gamma ,\dots $
; intuitively these will be partial functions on
![]() $\mathbb {N}$
. Individual variables
$\mathbb {N}$
. Individual variables
![]() $x, y, z,\dots $
will be taken to range over natural numbers. Numerical variables will always be taken to have denotations. There will also be a sort of variables
$x, y, z,\dots $
will be taken to range over natural numbers. Numerical variables will always be taken to have denotations. There will also be a sort of variables
![]() $f,g,h,\dots $
ranging over classical functions on
$f,g,h,\dots $
ranging over classical functions on
![]() $\mathbb {N}$
. These functions are extensional objects whose graph does not change over time.
$\mathbb {N}$
. These functions are extensional objects whose graph does not change over time.
We can assume in the background all the usual coding apparatus for finite sequences of natural numbers as found in, for instance, [Reference Hájek and Pudlák15]. This provides us with a formula
![]() $Seq(x)$
which is true of exactly those numbers x which code finite sequences; such numbers x are known as sequence numbers. It is sometimes also convenient to write
$Seq(x)$
which is true of exactly those numbers x which code finite sequences; such numbers x are known as sequence numbers. It is sometimes also convenient to write
![]() $x\in Seq$
rather than
$x\in Seq$
rather than
![]() $Seq(x)$
. We will write
$Seq(x)$
. We will write
![]() $\langle n_0,\dots ,n_k\rangle $
for the (code of) the finite sequence with
$\langle n_0,\dots ,n_k\rangle $
for the (code of) the finite sequence with
![]() $i^{th}$
member
$i^{th}$
member
![]() $n_{i-1}$
.
$n_{i-1}$
.
There are also length, projection, and concatenation functions for sequences. We will use
![]() $lh$
for the length function,
$lh$
for the length function,
![]() $(\cdot )_i$
for the projection function, and
$(\cdot )_i$
for the projection function, and
![]() $^\frown $
for concatenation. So if
$^\frown $
for concatenation. So if
![]() $x{\kern-1pt}={\kern-1pt}\langle x_0,\dots ,x_k \rangle $
, then
$x{\kern-1pt}={\kern-1pt}\langle x_0,\dots ,x_k \rangle $
, then
![]() $lh(x){\kern-1pt}={\kern-1pt}k+1$
, and for all
$lh(x){\kern-1pt}={\kern-1pt}k+1$
, and for all
![]() $i\leq k$
,
$i\leq k$
,
![]() $(x)_i=x_i$
. And if
$(x)_i=x_i$
. And if
![]() $x=\langle x_0,\dots ,x_k\rangle $
and
$x=\langle x_0,\dots ,x_k\rangle $
and
![]() $y=\langle y_0,\dots ,y_l\rangle $
, the concatenation
$y=\langle y_0,\dots ,y_l\rangle $
, the concatenation
![]() $x^\frown y:=\langle x_0,\dots ,x_k,y_0,\dots ,y_l\rangle $
. We will write
$x^\frown y:=\langle x_0,\dots ,x_k,y_0,\dots ,y_l\rangle $
. We will write
![]() $x\preceq y$
when
$x\preceq y$
when
![]() $x,y \in Seq$
and there is some
$x,y \in Seq$
and there is some
![]() $z\in Seq$
such that
$z\in Seq$
such that
![]() $y=x^\frown z$
. Finally, if
$y=x^\frown z$
. Finally, if
![]() $\vec {x}=\langle x_0,\dots ,x_{k-1}\rangle $
and
$\vec {x}=\langle x_0,\dots ,x_{k-1}\rangle $
and
![]() $\vec {y}=\langle y_0,\dots ,y_{k-1}\rangle $
are both k-tuples of sequence numbers, then we may write
$\vec {y}=\langle y_0,\dots ,y_{k-1}\rangle $
are both k-tuples of sequence numbers, then we may write
![]() $\vec {x}\preceq \vec {y}$
, understood to mean
$\vec {x}\preceq \vec {y}$
, understood to mean
![]() $x_0\preceq y_0 \wedge \dots \wedge x_{k-1} \preceq y_{k-1}$
.
$x_0\preceq y_0 \wedge \dots \wedge x_{k-1} \preceq y_{k-1}$
.
There are two important pieces of notation that are unique to the literature on choice sequences, though widespread within that literature. First,
![]() $\overline {\alpha }(x)$
is used to denote the initial segment of
$\overline {\alpha }(x)$
is used to denote the initial segment of
![]() $\alpha $
of length x. Thus,
$\alpha $
of length x. Thus,
![]() $\overline {\alpha }(x)=y$
iff
$\overline {\alpha }(x)=y$
iff
![]() $y\in Seq$
,
$y\in Seq$
,
![]() $lh(y)=x+1$
, and for all
$lh(y)=x+1$
, and for all
![]() $z\leq x$
,
$z\leq x$
,
![]() $\alpha (z)=(y)_z$
. Second, it is common to use
$\alpha (z)=(y)_z$
. Second, it is common to use
![]() $\alpha \in x$
as an abbreviation for
$\alpha \in x$
as an abbreviation for
![]() $\overline {\alpha }(lh(x))=x$
. What this means is that x is a sequence number encoding an initial segment of
$\overline {\alpha }(lh(x))=x$
. What this means is that x is a sequence number encoding an initial segment of
![]() $\alpha $
. I will also use
$\alpha $
. I will also use
![]() $\overline {f}$
and
$\overline {f}$
and
![]() $f\in n$
analogously when f is a classical function variable.
$f\in n$
analogously when f is a classical function variable.
The initial segment of
![]() $\alpha $
, symbolized is
$\alpha $
, symbolized is
![]() $\alpha $
will refer to the largest sequence number n such that
$\alpha $
will refer to the largest sequence number n such that
![]() $\alpha \in n$
, and
$\alpha \in n$
, and
![]() $\alpha $
is not (yet) defined on any greater arguments. In other words,
$\alpha $
is not (yet) defined on any greater arguments. In other words,
![]() $\mathrm {is}\alpha =n$
iff
$\mathrm {is}\alpha =n$
iff
![]() $\forall x< lh(n) \alpha (x)=(n)_x \wedge \forall x\geq lh(n) \alpha (x)\neq \alpha (x)$
.
$\forall x< lh(n) \alpha (x)=(n)_x \wedge \forall x\geq lh(n) \alpha (x)\neq \alpha (x)$
.
Finally, one more piece of notation stems from the fact that I will be using a free logic in what follows. Specifically, I will use a negative free logic, so any atom
![]() $Pt$
is true only if t denotes. Thus
$Pt$
is true only if t denotes. Thus
![]() $t=t$
can be used as an existence predicate. Let
$t=t$
can be used as an existence predicate. Let
![]() $t_1 \simeq t_2:\leftrightarrow (t_1=t_2 \vee (t_1 \neq t_1 \wedge t_2 \neq t_2))$
. In other words,
$t_1 \simeq t_2:\leftrightarrow (t_1=t_2 \vee (t_1 \neq t_1 \wedge t_2 \neq t_2))$
. In other words,
![]() $t_1\simeq t_2$
means that either
$t_1\simeq t_2$
means that either
![]() $t_1$
and
$t_1$
and
![]() $t_2$
are both defined and identical or neither is defined.
$t_2$
are both defined and identical or neither is defined.
Since Greek letters are being used for choice sequence variables, I will use
![]() $A,B,\dots $
as metavariables ranging over formulas. P will be a metavariable ranging over atomic formulas. I will use both
$A,B,\dots $
as metavariables ranging over formulas. P will be a metavariable ranging over atomic formulas. I will use both
![]() $A^{o_1}_{o_2}$
and
$A^{o_1}_{o_2}$
and
![]() $A[o_1 / o_2]$
to denote the result of replacing all free occurrences of
$A[o_1 / o_2]$
to denote the result of replacing all free occurrences of
![]() $o_1$
in A with
$o_1$
in A with
![]() $o_2$
.
$o_2$
.
4 The modal logic
The idea behind the modal theory of choice sequences is that choice sequences are intra-temporal mathematical objects, and we capture their temporal character using modal operators. The main modal operator will be
![]() $\square $
, intuitively meaning “at all times henceforth …,” as well as its dual
$\square $
, intuitively meaning “at all times henceforth …,” as well as its dual
![]() $\lozenge $
, “at some later time ….” By fiat, we can take the later than relation to be reflexive, so that henceforth includes the present moment. Obviously, later than is transitive, and we can take it that the flow of time is not cyclical, so that later than is antisymmetric. Since we cannot assume that the flow of time has any other structure, the appropriate modal logic to use will be S4. In addition to the usual box and diamond, however, we will want to add a further modal operator.
$\lozenge $
, “at some later time ….” By fiat, we can take the later than relation to be reflexive, so that henceforth includes the present moment. Obviously, later than is transitive, and we can take it that the flow of time is not cyclical, so that later than is antisymmetric. Since we cannot assume that the flow of time has any other structure, the appropriate modal logic to use will be S4. In addition to the usual box and diamond, however, we will want to add a further modal operator.
Our choice of S4 reflects the fact that there might be multiple incompatible futures, different branches of time, as it were. Reading the box and diamond as temporal operators,
![]() $\square A$
means that A holds at every time henceforth. And
$\square A$
means that A holds at every time henceforth. And
![]() $\lozenge A$
means that A holds at some future moment on some branch; in other words, A might hold in the future. To express several concepts in the modal theory of choice sequences, however, we need something further: we need to be able to say that A will eventually be true, no matter how the future evolves; on every future branch of time, there is a moment at which A is true. To express this notion, let us introduce the operator
$\lozenge A$
means that A holds at some future moment on some branch; in other words, A might hold in the future. To express several concepts in the modal theory of choice sequences, however, we need something further: we need to be able to say that A will eventually be true, no matter how the future evolves; on every future branch of time, there is a moment at which A is true. To express this notion, let us introduce the operator
![]() $\mathcal {I}A$
, pronounced “inevitably A”.Footnote
9
The logic that results from adding
$\mathcal {I}A$
, pronounced “inevitably A”.Footnote
9
The logic that results from adding
![]() $\mathcal {I}$
to S4 can be called
$\mathcal {I}$
to S4 can be called
![]() $\mathbf {S4}_{\mathcal {I}}$
.Footnote
10
$\mathbf {S4}_{\mathcal {I}}$
.Footnote
10
The definition of an
![]() $\mathbf {S4}_{\mathcal {I}}$
model is exactly the same as that of an S4 model, and the satisfaction clauses are exactly the same for the vocabulary
$\mathbf {S4}_{\mathcal {I}}$
model is exactly the same as that of an S4 model, and the satisfaction clauses are exactly the same for the vocabulary
![]() $\rightarrow ,\wedge ,\vee ,\neg ,\forall , \exists , \square ,\lozenge $
. The only thing we need to add is the clause for
$\rightarrow ,\wedge ,\vee ,\neg ,\forall , \exists , \square ,\lozenge $
. The only thing we need to add is the clause for
![]() $\mathcal {I}$
. This requires one more definition:
$\mathcal {I}$
. This requires one more definition:
Definition 4.1. In a model M, a chain above w is a set X of worlds linearly ordered by R, such that for all
![]() $u\in X$
,
$u\in X$
,
![]() $wRu$
. A chain X above w is maximal if there is no proper superset
$wRu$
. A chain X above w is maximal if there is no proper superset
![]() $Y\supset X$
that is also a chain above w.
$Y\supset X$
that is also a chain above w.
Now the satisfaction clause for
![]() $\mathcal {I}A$
is as follows:
$\mathcal {I}A$
is as follows:
-
•
 $M,w \models \mathcal {I} A$
iff for every maximal chain X above w there is a
$M,w \models \mathcal {I} A$
iff for every maximal chain X above w there is a
 $u\in X$
such that
$u\in X$
such that
 $M,u\models A$
.
$M,u\models A$
.
This condition is pictured in the image below: every path above w through the model M eventually intersects the set of A-worlds.

Although conservative over S4, the logic
![]() $\mathbf {S4}_{\mathcal {I}}$
is fairly strong, being unaxiomatizable.Footnote
11
Nevertheless, the following list of axiom is sufficient for the purposes of this paper, and as we will see in Section 7.Footnote
12
$\mathbf {S4}_{\mathcal {I}}$
is fairly strong, being unaxiomatizable.Footnote
11
Nevertheless, the following list of axiom is sufficient for the purposes of this paper, and as we will see in Section 7.Footnote
12
-
M0 The axioms and rules of negative free S4 with CBF. (For concreteness, axioms M0.0–M0.13 are provided in Appendix A.)
-
M1
 $\square (A \rightarrow B)\rightarrow (\mathcal {I}A \rightarrow \mathcal {I}B)$
.
$\square (A \rightarrow B)\rightarrow (\mathcal {I}A \rightarrow \mathcal {I}B)$
. -
M2
 $A \rightarrow \mathcal {I}A$
.
$A \rightarrow \mathcal {I}A$
. -
M3
 $\square A \rightarrow \neg \mathcal {I}\neg A$
.
$\square A \rightarrow \neg \mathcal {I}\neg A$
. -
M4
 $\mathcal {I}\mathcal {I}A \rightarrow \mathcal {I}A$
.
$\mathcal {I}\mathcal {I}A \rightarrow \mathcal {I}A$
. -
M5
 $\mathcal {I}\square A \rightarrow \square \mathcal {I}A$
.
$\mathcal {I}\square A \rightarrow \square \mathcal {I}A$
. -
M6
 $\mathcal {I}\forall o A \rightarrow \forall o \mathcal {I}A$
.
$\mathcal {I}\forall o A \rightarrow \forall o \mathcal {I}A$
. -
M7
 $\exists o \mathcal {I}A \rightarrow \mathcal {I}\exists o A$
.
$\exists o \mathcal {I}A \rightarrow \mathcal {I}\exists o A$
.
The reason for using a free logic is that, since choice are meant to grow with time, it might happen that, say,
![]() $\alpha (100)$
has not yet been defined. The Converse Barcan Formula, however, ensures that the domain is growing, so that once an object exists it will never disappear. Since we will be working in a many-sorted logic, we include instances of M6 and M7 where o is each sort of variable.
$\alpha (100)$
has not yet been defined. The Converse Barcan Formula, however, ensures that the domain is growing, so that once an object exists it will never disappear. Since we will be working in a many-sorted logic, we include instances of M6 and M7 where o is each sort of variable.
Just as the necessity operator
![]() $\square $
has the dual possibility operator
$\square $
has the dual possibility operator
![]() $\lozenge $
, definable as
$\lozenge $
, definable as
![]() $\neg \square \neg $
, so the inevitability operator also has a dual
$\neg \square \neg $
, so the inevitability operator also has a dual
![]() $\neg \mathcal {I}\neg $
. Although I will not introduce a primitive symbol for this dual, it expresses an important concept:
$\neg \mathcal {I}\neg $
. Although I will not introduce a primitive symbol for this dual, it expresses an important concept:
![]() $\neg \mathcal {I}\neg A$
means, intuitively, that there is some possible path through the future such that A holds at every time on that path. This could be glossed in English as “it is possible that A holds into perpetuity”. I also want to draw attention to a derivable schema governing
$\neg \mathcal {I}\neg A$
means, intuitively, that there is some possible path through the future such that A holds at every time on that path. This could be glossed in English as “it is possible that A holds into perpetuity”. I also want to draw attention to a derivable schema governing
![]() $\mathcal {I} $
and
$\mathcal {I} $
and
![]() $\neg \mathcal {I}\neg $
, which I will appeal to later.
$\neg \mathcal {I}\neg $
, which I will appeal to later.
Proposition 4.2.
![]() $\vdash _{\mathbf {S4}_{\mathcal {I}}} (\mathcal {I}A \wedge \neg \mathcal {I}\neg B ) \rightarrow \lozenge (A\wedge B)$
.
$\vdash _{\mathbf {S4}_{\mathcal {I}}} (\mathcal {I}A \wedge \neg \mathcal {I}\neg B ) \rightarrow \lozenge (A\wedge B)$
.
Proof I prove the contrapositive.

With
![]() $\mathbf {S4}_{\mathcal {I}}$
as our background logic, we can turn now to developing the modal theory of lawless sequences.
$\mathbf {S4}_{\mathcal {I}}$
as our background logic, we can turn now to developing the modal theory of lawless sequences.
5 The modal theory of lawless sequences
Our language will be that of second-order arithmetic:
![]() $\lbrace 0,S,+,\times ,< \rbrace $
. The logical vocabulary is
$\lbrace 0,S,+,\times ,< \rbrace $
. The logical vocabulary is
![]() $ \lbrace \forall , \exists , \wedge ,\vee ,\rightarrow ,\neg ,=,\square , \mathcal {I} \rbrace $
. The possibility operator
$ \lbrace \forall , \exists , \wedge ,\vee ,\rightarrow ,\neg ,=,\square , \mathcal {I} \rbrace $
. The possibility operator
![]() $\lozenge $
can of course be defined as
$\lozenge $
can of course be defined as
![]() $\lozenge A:\leftrightarrow \neg \square \neg A$
.
$\lozenge A:\leftrightarrow \neg \square \neg A$
.
There are three sorts of variables:
![]() $x,y,z,\dots $
ranging over natural numbers,
$x,y,z,\dots $
ranging over natural numbers,
![]() $f,g,h,\dots $
ranging over classical functions on natural numbers, and
$f,g,h,\dots $
ranging over classical functions on natural numbers, and
![]() $\alpha ,\beta ,\gamma ,\dots $
ranging over choice sequences. The objects in the range of first-order variables
$\alpha ,\beta ,\gamma ,\dots $
ranging over choice sequences. The objects in the range of first-order variables
![]() $x,y,z,\dots $
are the familiar natural numbers. I assume that the natural numbers form a completed totality rather than themselves being a mere potential infinity. Thus the natural numbers all exist at each moment in time rather than coming to exist at some point in time. Functions
$x,y,z,\dots $
are the familiar natural numbers. I assume that the natural numbers form a completed totality rather than themselves being a mere potential infinity. Thus the natural numbers all exist at each moment in time rather than coming to exist at some point in time. Functions
![]() $f,g,h,\dots $
are the extensional objects familiar from classical second-order arithmetic, and their graphs are assumed to never change, being fixed for all time. I will occasionally use variables
$f,g,h,\dots $
are the extensional objects familiar from classical second-order arithmetic, and their graphs are assumed to never change, being fixed for all time. I will occasionally use variables
![]() $X,Y,Z$
for sets of natural numbers, though officially such sets are identified with their characteristic functions. The reason for taking functions as primitive and sets as defined, instead of the other way around, is that the intuitionistic theory of lawless sequences is formulated with variables for lawlike functions. These will be translated as classical function variables; so taking function variables to be primitive rather than defined simplifies the translation.
$X,Y,Z$
for sets of natural numbers, though officially such sets are identified with their characteristic functions. The reason for taking functions as primitive and sets as defined, instead of the other way around, is that the intuitionistic theory of lawless sequences is formulated with variables for lawlike functions. These will be translated as classical function variables; so taking function variables to be primitive rather than defined simplifies the translation.
Since choice sequences are supposed to be uncompleted objects, they should be partial functions of natural numbers. This will require our logic to be free, as indicated above.
For some purposes, we will be interested in formulas that contain no occurrences of choice sequence variables or modal operators, that is, formulas in the language of second-order arithmetic. Let this restricted language be denoted by
![]() $\mathcal {L}_0$
.
$\mathcal {L}_0$
.
We can separate the axioms of the theory into three categories: logical axioms, arithmetic axioms, and sequence axioms. The logical axioms will be those of
![]() $\mathbf {S4}_{\mathcal {I}}$
given above.
$\mathbf {S4}_{\mathcal {I}}$
given above.
5.1 Arithmetical axioms
For arithmetic axioms we include necessitations of universal closures of the following:
-
A0
 $0=0 \wedge (S(x)=S(x))\wedge (x+y=x+y) \wedge (x\times y =x\times y)$
.
$0=0 \wedge (S(x)=S(x))\wedge (x+y=x+y) \wedge (x\times y =x\times y)$
. -
A1
 $0\neq S(x)$
.
$0\neq S(x)$
. -
A2
 $S(x)=S(y) \rightarrow x=y$
.
$S(x)=S(y) \rightarrow x=y$
. -
A3
 $x+0=x$
.
$x+0=x$
. -
A4
 $x+S(y)=S(x+y)$
.
$x+S(y)=S(x+y)$
. -
A5
 $x\times 0=0$
.
$x\times 0=0$
. -
A6
 $x\times S(y)= (x\times y) +x$
.
$x\times S(y)= (x\times y) +x$
. -
A7
 $x\nless 0$
.
$x\nless 0$
. -
A8
 $x<S(y)\leftrightarrow (x<y \vee x=y)$
.
$x<S(y)\leftrightarrow (x<y \vee x=y)$
. -
A9
 $\square \forall x \exists y \square f(x)=y$
.
$\square \forall x \exists y \square f(x)=y$
. -
IND
 $\forall f \big ( f(0)=0 \wedge \forall x(f(x)=0 \rightarrow f(S(x))=0 ) \rightarrow \forall x f(x)=0 \big )$
.
$\forall f \big ( f(0)=0 \wedge \forall x(f(x)=0 \rightarrow f(S(x))=0 ) \rightarrow \forall x f(x)=0 \big )$
.
In the presence of the full axiom of choice, the induction axiom IND also entails each instance of the induction schema, for A an
![]() $\mathcal {L}_0$
formula:
$\mathcal {L}_0$
formula:
Conversely, the schema also entails the axiom IND by taking the instance
![]() $A(x):= f(x)=0$
. Of course, in various subsystems of second-order arithmetic that we will return to in Section 9, the difference between the induction axiom and the induction schema is important.
$A(x):= f(x)=0$
. Of course, in various subsystems of second-order arithmetic that we will return to in Section 9, the difference between the induction axiom and the induction schema is important.
A0 is included to ensure that arithmetical terms always have a denotation, and A9 ensures that classical functions are always defined and have their values necessarily. Otherwise these are the standard axioms of PA. We also include every instance of the axiom of choice where A is an
![]() $\mathcal {L}_0$
formula:
$\mathcal {L}_0$
formula:
-
AC
 $\forall x \exists y A(x,y) \rightarrow \exists f \square \forall x \square A(x,f(x))$
.
$\forall x \exists y A(x,y) \rightarrow \exists f \square \forall x \square A(x,f(x))$
.
This of course entails the comprehension schema for sets of numbers (where, again, A is an
![]() $\mathcal {L}_0$
formula):
$\mathcal {L}_0$
formula):
-
CA
 $ \exists X \square \forall x(x\in X \leftrightarrow A(x))$
.
$ \exists X \square \forall x(x\in X \leftrightarrow A(x))$
.
The reason for not allowing choice sequence variables to occur in the choice schema is that, per axiom A9, we want our functions to not change with time. If we allowed choice sequences to occur in the choice schema, we could define a function f such that
![]() $\forall x (\alpha (x)=f(x) \vee (\alpha (x)\neq \alpha (x) \wedge f(x)=0)$
. But then f would be subject to change as
$\forall x (\alpha (x)=f(x) \vee (\alpha (x)\neq \alpha (x) \wedge f(x)=0)$
. But then f would be subject to change as
![]() $\alpha $
grew, which we do not want.
$\alpha $
grew, which we do not want.
(The reason for allowing all instances of AC and the full induction schema will be discussed in Section 8.3. For most purposes in this paper, however, choice for
![]() $\Delta ^0_1$
formulas would suffice.)
$\Delta ^0_1$
formulas would suffice.)
Given that the goal of this paper is to combine a modal-potentialist construal of lawless sequences with a standard, classical theory of second-order arithmetic, we want the arithmetic portion of the theory to hold constant through all time. This idea of a formula holding constant through time is captured by the notion of stability.
Definition 5.1 (Stability).
Say that a formula A is positively stable when the following holds:
And A is negatively stable when:
A formula that is both positively and negatively stable will be called stable simpliciter.
Thus, to say that a formula A is provably stable in a theory T is to say that T proves these two conditionals. Similarly, a model in which those two conditionals are true would be a model in which A is stable.
There are at least three natural ways to ensure that the arithmetic portion of the theory is provably stable. The first way is simply to add as axioms the positive and negative stability of all
![]() $\mathcal {L}_0$
formulas. The second option appeals to the full axiom of choice. The third option uses AC restricted to atomic
$\mathcal {L}_0$
formulas. The second option appeals to the full axiom of choice. The third option uses AC restricted to atomic
![]() $\mathcal {L}_0$
formulas and the Barcan formula for individual and classical function variables. The Barcan formula, recall, is the schema
$\mathcal {L}_0$
formulas and the Barcan formula for individual and classical function variables. The Barcan formula, recall, is the schema
![]() $ \forall o \square A(o) \rightarrow \square \forall o A(o) $
.
$ \forall o \square A(o) \rightarrow \square \forall o A(o) $
.
Proposition 5.2. Assume the axioms A0–A9. Then:
-
1. Assuming full AC, each
 $\mathcal {L}_0$
formula A is provably stable.
$\mathcal {L}_0$
formula A is provably stable. -
2. Assuming the Barcan Formula for individual variables and classical function variables and AC restricted to atomic formulas, each
 $\mathcal {L}_0$
formula A is provably stable.
$\mathcal {L}_0$
formula A is provably stable.
Proof (1) Given any
![]() $\mathcal {L}_0$
formula A, AC entails that there is a function:
$\mathcal {L}_0$
formula A, AC entails that there is a function:
 $$ \begin{align*}f_A(\vec{x})= \begin{cases} 1, & \mathrm{if~} A(\vec{x}), \\ 0, & \mathrm{if~} \neg A(\vec{x}). \end{cases}\end{align*} $$
$$ \begin{align*}f_A(\vec{x})= \begin{cases} 1, & \mathrm{if~} A(\vec{x}), \\ 0, & \mathrm{if~} \neg A(\vec{x}). \end{cases}\end{align*} $$
Now by A9,
![]() $f_A$
has its values necessarily. So if A, then
$f_A$
has its values necessarily. So if A, then
![]() $f_A(\vec{x})=1$
, hence
$f_A(\vec{x})=1$
, hence
![]() $\square f_A(\vec {x})=1$
, hence
$\square f_A(\vec {x})=1$
, hence
![]() $\square A(\vec {x})$
. Similarly if
$\square A(\vec {x})$
. Similarly if
![]() $\neg A(\vec {x})$
.
$\neg A(\vec {x})$
.
(2) Induction on the complexity of A. For the atomic case, use AC as in the proof of (1). For the induction step, the cases where A is
![]() $\neg B$
,
$\neg B$
,
![]() $B\vee C$
,
$B\vee C$
,
![]() $B\wedge C$
, or
$B\wedge C$
, or
![]() $B\rightarrow C$
are all straightforward using the i.h. Consider the case where A is
$B\rightarrow C$
are all straightforward using the i.h. Consider the case where A is
![]() $\forall y B$
. By i.h. (suppressing other free variables for readability) we have a proof of
$\forall y B$
. By i.h. (suppressing other free variables for readability) we have a proof of
![]() $\forall y(B \rightarrow \square B)$
, which gives
$\forall y(B \rightarrow \square B)$
, which gives
![]() $\forall y B \rightarrow \forall y \square B$
, which by the Barcan Formula gives
$\forall y B \rightarrow \forall y \square B$
, which by the Barcan Formula gives
![]() $\forall y B\rightarrow \square \forall y B$
. This shows A is positively stable.
$\forall y B\rightarrow \square \forall y B$
. This shows A is positively stable.
For negative stability, by the i.h. we have
![]() $\forall y(\neg B \rightarrow \square \neg B)$
, which entails
$\forall y(\neg B \rightarrow \square \neg B)$
, which entails
![]() $\exists y \neg B \rightarrow \exists y \square \neg B)$
, which entails
$\exists y \neg B \rightarrow \exists y \square \neg B)$
, which entails
![]() $\neg \forall y B \rightarrow \square \neg \forall y B$
.
$\neg \forall y B \rightarrow \square \neg \forall y B$
.
The cases of
![]() $\exists x B$
,
$\exists x B$
,
![]() $\forall f B$
, and
$\forall f B$
, and
![]() $\exists f B$
are similar.
$\exists f B$
are similar.
Each of these three ways of ensuring the stability of
![]() $\mathcal {L}_0$
formulas is well-motivated. For instance, because arithmetic stability falls straightforwardly out of the main goal of this paper, it would not be unreasonable to simply stipulate it axiomatically. Likewise, the idea that the realm of numbers and classical functions on them is fixed and unchanging suggests adopting the Barcan Formula.Footnote
13
$\mathcal {L}_0$
formulas is well-motivated. For instance, because arithmetic stability falls straightforwardly out of the main goal of this paper, it would not be unreasonable to simply stipulate it axiomatically. Likewise, the idea that the realm of numbers and classical functions on them is fixed and unchanging suggests adopting the Barcan Formula.Footnote
13
Since I already stipulated that we have the full AC available, we could simply leave the matter there. In Sections 8.3 and 9, however, I will return to the question of whether one could use weaker versions of AC; in that context, we would need to have a different way of proving stability for
![]() $\mathcal {L}_0$
formulas.
$\mathcal {L}_0$
formulas.
5.2 Sequence axioms
For sequence axioms we include nine axioms. The first five axioms stem simply from the picture of an agent creating choice sequences and are not particular to lawless sequences. The first four of these are:
-
S1
 $\exists n\in Seq ~ \mathrm {is}\alpha =n$
.
$\exists n\in Seq ~ \mathrm {is}\alpha =n$
. -
S2
 $\square \forall x \mathcal {I} \exists y \alpha (x)=y$
.
$\square \forall x \mathcal {I} \exists y \alpha (x)=y$
. -
S3
 $\square (\forall x\forall y(\alpha (x)=y \rightarrow \square \alpha (x)=y) )$
.
$\square (\forall x\forall y(\alpha (x)=y \rightarrow \square \alpha (x)=y) )$
. -
S4
 $\square \exists \alpha \forall x \forall y \neg \alpha (x)= y$
.
$\square \exists \alpha \forall x \forall y \neg \alpha (x)= y$
.
The first two axioms ensure that the choice sequences are growing with time, and there is no end of time. The third axiom says that when the value of a choice sequence has been chosen, it is fixed for all time. The fourth axiom says that there is always a choice sequence that is not yet defined on any argument; informally this is justified because an agent defining sequences of natural numbers could always start a new sequence.
The fifth axiom requires defining some new notions. I will say an
![]() $\mathcal {L}_0$
formula A is quasi-treelike if
$\mathcal {L}_0$
formula A is quasi-treelike if
![]() $A(x)$
implies that x is a k-tuple of sequence numbers and that if
$A(x)$
implies that x is a k-tuple of sequence numbers and that if
![]() $A(\langle m_1,\dots ,m_k \rangle ) $
and
$A(\langle m_1,\dots ,m_k \rangle ) $
and
![]() $n_1 \preceq m_1,\dots , n_k\preceq m_k$
then
$n_1 \preceq m_1,\dots , n_k\preceq m_k$
then
![]() $A(\langle n_1,\dots ,n_k\rangle )$
. Symbolize this claim as
$A(\langle n_1,\dots ,n_k\rangle )$
. Symbolize this claim as
![]() $qTree^k(A)$
. We can define the ordering
$qTree^k(A)$
. We can define the ordering
![]() $\leq _A$
as
$\leq _A$
as
![]() $\preceq \upharpoonright A$
. The strict relation
$\preceq \upharpoonright A$
. The strict relation
![]() $<_A$
is defined in the usual way. Obviously, if there is a set
$<_A$
is defined in the usual way. Obviously, if there is a set
![]() $T=\lbrace x: A(x)\rbrace $
, then
$T=\lbrace x: A(x)\rbrace $
, then
![]() $(T,\leq _T)$
will be a partial order, and each of its projections
$(T,\leq _T)$
will be a partial order, and each of its projections
![]() $T_i=\lbrace n_i : \exists \langle n_1,\dots , n_i,\dots ,n_k \rangle \in T \rbrace $
will be a tree. Nevertheless, we will be interested in quasi-treelike formulas and treat them schematically, irrespective of whether they actually form a set or not. As usual, I will say that A is well-founded (in symbols:
$T_i=\lbrace n_i : \exists \langle n_1,\dots , n_i,\dots ,n_k \rangle \in T \rbrace $
will be a tree. Nevertheless, we will be interested in quasi-treelike formulas and treat them schematically, irrespective of whether they actually form a set or not. As usual, I will say that A is well-founded (in symbols:
![]() $WF(<_A)$
), when there is no infinite path through A, that is, there is no function f such that for all x,
$WF(<_A)$
), when there is no infinite path through A, that is, there is no function f such that for all x,
![]() $f(x+1)>_A f(x)$
. With these notions in place, the fifth axiom says that if any arithmetic formula A is quasi-treelike and well-founded, then any k choice sequences will inevitably leave T:
$f(x+1)>_A f(x)$
. With these notions in place, the fifth axiom says that if any arithmetic formula A is quasi-treelike and well-founded, then any k choice sequences will inevitably leave T:
-
S5
 $qTree^k(A) \wedge WF(<_A) \rightarrow \mathcal {I} \exists x_1\dots \exists x_k \left ( \bigwedge _i\mathrm {is} \alpha _i=x_i \wedge \neg A(\langle x_1,\dots ,x_k\rangle ) \right )$
.
$qTree^k(A) \wedge WF(<_A) \rightarrow \mathcal {I} \exists x_1\dots \exists x_k \left ( \bigwedge _i\mathrm {is} \alpha _i=x_i \wedge \neg A(\langle x_1,\dots ,x_k\rangle ) \right )$
.
The justification for this axiom is easiest to articulate in the case
![]() $k=1$
, so that A is just a (schematic definition of a) well-founded tree. A well-founded tree has only finite branches, whereas a choice sequence grows infinitely far and so must eventually outgrow the tree. The generalization to
$k=1$
, so that A is just a (schematic definition of a) well-founded tree. A well-founded tree has only finite branches, whereas a choice sequence grows infinitely far and so must eventually outgrow the tree. The generalization to
![]() $k>1$
would be more verbose, but is conceptually straightforward. This is an important axiom because, in effect, it allows us to prove things about choice sequences by transfinite induction, which none of the other axioms do. (The induction-like character of this axiom comes from the similarity between this axiom and bar induction.)
$k>1$
would be more verbose, but is conceptually straightforward. This is an important axiom because, in effect, it allows us to prove things about choice sequences by transfinite induction, which none of the other axioms do. (The induction-like character of this axiom comes from the similarity between this axiom and bar induction.)
The remaining four axioms pertain specifically to lawless sequences. (Recall that
![]() $t_1\simeq t_2$
means that either
$t_1\simeq t_2$
means that either
![]() $t_1$
and
$t_1$
and
![]() $t_2$
are both defined and identical or neither is defined.)
$t_2$
are both defined and identical or neither is defined.)
-
S6
 $\square \forall n \in Seq \mathcal {I} \exists \alpha (\alpha \in n)$
.
$\square \forall n \in Seq \mathcal {I} \exists \alpha (\alpha \in n)$
. -
S7
 $\neg \square \forall x \alpha (x)\simeq \beta (x)\rightarrow \square \neg \square \forall x \alpha (x)\simeq \beta (x)$
.
$\neg \square \forall x \alpha (x)\simeq \beta (x)\rightarrow \square \neg \square \forall x \alpha (x)\simeq \beta (x)$
. -
S8
 $ \bigwedge _{i\neq j} \neg \square \forall x \alpha _i(x){\kern-1.3pt}\simeq{\kern-1.3pt} \alpha _j(x) {\kern-1.3pt}\rightarrow{\kern-1.3pt} [ \neg \exists x_1 \exists y_1 \dots \exists x_k \exists y_k {\kern-1.2pt}\bigwedge _{i\leqslant k} \alpha _i(x_i)=y_i {\kern-1pt}\wedge f_i(x_i){\kern-1pt}\neq{\kern-1pt} y_i {\kern-1pt}\rightarrow{\kern-1pt} \neg \mathcal {I} \exists x_1 \exists y_1 \dots \exists x_k \exists y_k \bigvee _{i\leqslant k} \alpha _i(x_i){\kern-1pt}={\kern-1pt}y_i \wedge f_i(x_i){\kern-1pt}\neq{\kern-1pt} y_i ]$
.
$ \bigwedge _{i\neq j} \neg \square \forall x \alpha _i(x){\kern-1.3pt}\simeq{\kern-1.3pt} \alpha _j(x) {\kern-1.3pt}\rightarrow{\kern-1.3pt} [ \neg \exists x_1 \exists y_1 \dots \exists x_k \exists y_k {\kern-1.2pt}\bigwedge _{i\leqslant k} \alpha _i(x_i)=y_i {\kern-1pt}\wedge f_i(x_i){\kern-1pt}\neq{\kern-1pt} y_i {\kern-1pt}\rightarrow{\kern-1pt} \neg \mathcal {I} \exists x_1 \exists y_1 \dots \exists x_k \exists y_k \bigvee _{i\leqslant k} \alpha _i(x_i){\kern-1pt}={\kern-1pt}y_i \wedge f_i(x_i){\kern-1pt}\neq{\kern-1pt} y_i ]$
. -
S9
 $\bigwedge _{i\neq j } \neg \square \forall x \alpha _i(x) \simeq \alpha _j(x) \wedge \bigwedge _{i\leqslant k} \mathrm {is} \alpha _i=n_i\\ \rightarrow \forall m_1\in Seq \dots \forall m_k\in Seq \, \lozenge \bigwedge _{i\leqslant k} \mathrm {is} \alpha_i =n_i^\frown m_i $
.
$\bigwedge _{i\neq j } \neg \square \forall x \alpha _i(x) \simeq \alpha _j(x) \wedge \bigwedge _{i\leqslant k} \mathrm {is} \alpha _i=n_i\\ \rightarrow \forall m_1\in Seq \dots \forall m_k\in Seq \, \lozenge \bigwedge _{i\leqslant k} \mathrm {is} \alpha_i =n_i^\frown m_i $
.
The sixth axiom says that for every possible initial segment of a choice sequence, there will inevitably eventually be a choice sequence with that segment. There are two motivating ideas behind this axiom. The first is that it should be possible that there is a lawless sequence with any given initial segment. If the sequences are lawless, then no initial segment should be ruled out from the beginning. The second idea is that we want our universe of choice sequences to be maximally inclusive: anything that can happen should happen. The idealized mathematician should do everything that they can do. In this sense, S6 combines an insight about what is possible for lawless sequences with a maximality principle about how many lawless sequences eventually get created in the course of time.
The seventh axiom says that if
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are distinct, then they are necessarily distinct.
$\beta $
are distinct, then they are necessarily distinct.
The eighth axiom is a schema, with one instance for each value of k. The
![]() $k=1$
instance says that if
$k=1$
instance says that if
![]() $\alpha $
and f agree on the arguments for which
$\alpha $
and f agree on the arguments for which
![]() $\alpha $
is so far defined, there is no guarantee that
$\alpha $
is so far defined, there is no guarantee that
![]() $\alpha $
and f will ever disagree. The motivation for this axiom is similar to the first part of the motivation for axiom S4: if there were a guarantee that
$\alpha $
and f will ever disagree. The motivation for this axiom is similar to the first part of the motivation for axiom S4: if there were a guarantee that
![]() $\alpha $
would eventually disagree with f, then a path following f would be outlawed or off limits, contradicting the idea that the sequences in question are lawless. Alongside S5, S8 is one of the most important axioms and is at the heart of several arguments that follow. These two particular axioms are important because they provide a bridge between the existence of classical functions and the behavior of choice sequences.
$\alpha $
would eventually disagree with f, then a path following f would be outlawed or off limits, contradicting the idea that the sequences in question are lawless. Alongside S5, S8 is one of the most important axioms and is at the heart of several arguments that follow. These two particular axioms are important because they provide a bridge between the existence of classical functions and the behavior of choice sequences.
The ninth axiom says that given any k distinct lawless sequences that currently have initial segments
![]() $n_1,\dots ,n_k$
, they could be extended to have any possible initial segments
$n_1,\dots ,n_k$
, they could be extended to have any possible initial segments
![]() $n_1^\frown m_1,\dots , n_k^\frown m_k$
. (This is again really a schema, with one instance for each k.) This axiom combines two ideas. The first is that for any single lawless sequence
$n_1^\frown m_1,\dots , n_k^\frown m_k$
. (This is again really a schema, with one instance for each k.) This axiom combines two ideas. The first is that for any single lawless sequence
![]() $\alpha $
, if it currently has the initial segment n, then there is nothing to preclude it going on to have the initial segment
$\alpha $
, if it currently has the initial segment n, then there is nothing to preclude it going on to have the initial segment
![]() $n^\frown m$
. The second idea is that whenever some initial segments are individually possible for sequences
$n^\frown m$
. The second idea is that whenever some initial segments are individually possible for sequences
![]() $\alpha _1,\dots ,\alpha _k$
, then they are jointly compossible—they can all be realized at once.
$\alpha _1,\dots ,\alpha _k$
, then they are jointly compossible—they can all be realized at once.
Definition 5.3 (
 $MC_{LS}$
).
$MC_{LS}$
).
Let
![]() $MC_{LS}$
be the theory based on the logic
$MC_{LS}$
be the theory based on the logic
![]() $\mathbf {S4}_{\mathcal {I}}$
that consists of axioms A0–A9, IND, AC, axioms asserting the stability of
$\mathbf {S4}_{\mathcal {I}}$
that consists of axioms A0–A9, IND, AC, axioms asserting the stability of
![]() $\mathcal {L}_0$
formulas, and axioms S1–S9.
$\mathcal {L}_0$
formulas, and axioms S1–S9.
The name is chosen because it is a Modal theory of Choice sequences restricted to Lawless Sequences.
Although we are working in a free logic and there will be terms that may not denote, it will be true that each term eventually acquires a denotation.
Proposition 5.4. For any term t:
-
1. If t does not contain any choice sequence variables, then
 $MC_{LS}\vdash \square \forall \vec {x} \forall \vec {f}\,(t(\vec {x},\vec {f})=t(\vec {x},\vec {f}))$
.
$MC_{LS}\vdash \square \forall \vec {x} \forall \vec {f}\,(t(\vec {x},\vec {f})=t(\vec {x},\vec {f}))$
. -
2. If t does contain some choice sequence variables, then
 $MC_{LS}\vdash \forall \vec {\alpha } \forall \vec {x} \forall \vec {f} \mathcal {I} [ t(\vec {\alpha },\vec {x},\vec {f})=t(\vec {\alpha },\vec {x},\vec {f}) ]$
.
$MC_{LS}\vdash \forall \vec {\alpha } \forall \vec {x} \forall \vec {f} \mathcal {I} [ t(\vec {\alpha },\vec {x},\vec {f})=t(\vec {\alpha },\vec {x},\vec {f}) ]$
.
Proof (1) Induction on the complexity of t. For the basis case, if t is a free variable this holds by logic. If t is 0, this holds by A0. The induction step follows from A0 and the i.h. or A9 and the i.h.
(2) Induction on complexity. In the basis case, we know
![]() $t=t$
by claim (1). For the induction step, if t is
$t=t$
by claim (1). For the induction step, if t is
![]() $f(t_0)$
, then by i.h. we know
$f(t_0)$
, then by i.h. we know
![]() $\mathcal {I}\exists x(x=t_0)$
, and hence by A9,
$\mathcal {I}\exists x(x=t_0)$
, and hence by A9,
![]() $\mathcal {I}\exists y f(t_0)=y$
. If t is
$\mathcal {I}\exists y f(t_0)=y$
. If t is
![]() $\alpha (t_0)$
, then by i.h. we know
$\alpha (t_0)$
, then by i.h. we know
![]() $\mathcal {I}\exists x(x=t_0)$
, so by S2,
$\mathcal {I}\exists x(x=t_0)$
, so by S2,
![]() $\mathcal {I}\mathcal {I} \exists y \alpha (t_0)=y$
, which entails
$\mathcal {I}\mathcal {I} \exists y \alpha (t_0)=y$
, which entails
![]() $\mathcal {I} \exists y \alpha (t_0)=y$
.
$\mathcal {I} \exists y \alpha (t_0)=y$
.
6 The intuitionistic theory of lawless sequences
In this section I will introduce the intuitionistic theory of lawless sequences; then in the next two sections I will show that this theory can be interpreted in
![]() $MC_{LS}$
. Because this theory is not very well known outside intuitionistic circles, I will both present the precise axioms of lawless sequences and also discuss their informal motivation. (The intuitionistic theory
$MC_{LS}$
. Because this theory is not very well known outside intuitionistic circles, I will both present the precise axioms of lawless sequences and also discuss their informal motivation. (The intuitionistic theory
![]() $LS$
of lawless sequence results from adding these axioms to a simple base theory of analysis. I will return to that base theory in Section 8.3, but for now the focus will be on the axioms peculiar to lawless sequences.) My exposition here largely follows [Reference Troelstra31, Chapter 2] and [Reference Troelstra and van Dalen34, Chapter 12], and the reader familiar with those references may skim or skip this section.
$LS$
of lawless sequence results from adding these axioms to a simple base theory of analysis. I will return to that base theory in Section 8.3, but for now the focus will be on the axioms peculiar to lawless sequences.) My exposition here largely follows [Reference Troelstra31, Chapter 2] and [Reference Troelstra and van Dalen34, Chapter 12], and the reader familiar with those references may skim or skip this section.
To reduce clutter, in this section only I will use
![]() $n,m$
as variables ranging over sequence numbers, so that if
$n,m$
as variables ranging over sequence numbers, so that if
![]() $Seq$
is the set of sequences numbers,
$Seq$
is the set of sequences numbers,
![]() $\forall n$
and
$\forall n$
and
![]() $\exists n$
should be taken as abbreviating
$\exists n$
should be taken as abbreviating
![]() $\forall n\in Seq$
and
$\forall n\in Seq$
and
![]() $\exists n\in Seq$
.
$\exists n\in Seq$
.
There are four axioms of this theory, which I will discuss in turn. The first axiom says that for every possible initial segment, there is a lawless sequence with that initial segment.
-
LS1
 $\forall n \exists \alpha (\alpha \in n)$
$\forall n \exists \alpha (\alpha \in n)$
Similar to the axiom S6 in my modal theory,
![]() $LS1$
serves as a density principle. Troelstra also describes it as corresponding to the informal idea that we can pick any initial segment of a sequence before we let it proceed on its own.
$LS1$
serves as a density principle. Troelstra also describes it as corresponding to the informal idea that we can pick any initial segment of a sequence before we let it proceed on its own.
The second axiom says that (extensional) identity is decidable for lawless sequences, where extensional identity
![]() $\alpha =\beta $
is understood to mean
$\alpha =\beta $
is understood to mean
![]() $\forall x (\alpha (x)=\beta (x))$
.
$\forall x (\alpha (x)=\beta (x))$
.
-
LS2
 $\alpha = \beta \vee \alpha \neq \beta $
$\alpha = \beta \vee \alpha \neq \beta $
This axiom is justified by reference to intensional identity: two segments are intensionally identical (written
![]() $\alpha \equiv \beta $
) if they are given as the very same procedure for picking numbers. Intuitively, intensional identity should be decidable. So if we can argue that
$\alpha \equiv \beta $
) if they are given as the very same procedure for picking numbers. Intuitively, intensional identity should be decidable. So if we can argue that
![]() $\alpha = \beta \leftrightarrow \alpha \equiv \beta $
, then it would follow that extensional identity is decidable. Clearly
$\alpha = \beta \leftrightarrow \alpha \equiv \beta $
, then it would follow that extensional identity is decidable. Clearly
![]() $\alpha \equiv \beta \rightarrow \alpha =\beta $
. Conversely, since at any stage of picking, one only knows a finite initial segment of a sequence, the only way one could know two sequences are (always) coextensive is if they are given as the very same sequence of choices. Hence
$\alpha \equiv \beta \rightarrow \alpha =\beta $
. Conversely, since at any stage of picking, one only knows a finite initial segment of a sequence, the only way one could know two sequences are (always) coextensive is if they are given as the very same sequence of choices. Hence
![]() $\alpha =\beta \rightarrow \alpha \equiv \beta $
. Note that this is an intuitionistic argument. It asks what it would take to prove
$\alpha =\beta \rightarrow \alpha \equiv \beta $
. Note that this is an intuitionistic argument. It asks what it would take to prove
![]() $\alpha =\beta $
and concludes that one would have to have proved
$\alpha =\beta $
and concludes that one would have to have proved
![]() $\alpha \equiv \beta $
. Moreover, it does not rely on the “unfinished” character of choice sequences, for even if we think of lawless sequences as already completed by the ideal mathematician, our inability to survey the entire sequence, or predict its course via a law, would preclude us from asserting
$\alpha \equiv \beta $
. Moreover, it does not rely on the “unfinished” character of choice sequences, for even if we think of lawless sequences as already completed by the ideal mathematician, our inability to survey the entire sequence, or predict its course via a law, would preclude us from asserting
![]() $\alpha =\beta $
unless we had a proof of
$\alpha =\beta $
unless we had a proof of
![]() $\alpha \equiv \beta $
.
$\alpha \equiv \beta $
.
The third axiom says that any property A which holds of a lawless sequence
![]() $\alpha $
depends only on some finite initial segment of
$\alpha $
depends only on some finite initial segment of
![]() $\alpha $
. Thus, the third axiom justifies a continuity principle for mappings from lawless sequences to numbers.
$\alpha $
. Thus, the third axiom justifies a continuity principle for mappings from lawless sequences to numbers.
-
LS3
 $A(\alpha ,\beta _1,\dots ,\beta _l) \wedge \bigwedge _i \alpha \neq \beta _i \rightarrow \exists n ( \alpha \in n \wedge \forall \gamma \in n (\bigwedge _i \gamma \neq \beta _i \rightarrow A(\gamma ,\beta _1,\dots ,\beta _l)))$
$A(\alpha ,\beta _1,\dots ,\beta _l) \wedge \bigwedge _i \alpha \neq \beta _i \rightarrow \exists n ( \alpha \in n \wedge \forall \gamma \in n (\bigwedge _i \gamma \neq \beta _i \rightarrow A(\gamma ,\beta _1,\dots ,\beta _l)))$
This is justified by the idea that anything that can be asserted about a lawless sequence is asserted at some finite stage, and hence is asserted on the basis of only a finite segment of the sequence. Thus the assertion should also hold of any sequence with that same initial finite segment. This is often called the axiom of open data.
The reason for requiring that
![]() $\alpha $
be distinct from the
$\alpha $
be distinct from the
![]() $\beta $
’s is to rule out counterexamples that rely on
$\beta $
’s is to rule out counterexamples that rely on
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
being identical. For instance, if A were the simple formula
$\beta $
being identical. For instance, if A were the simple formula
![]() $\alpha =\beta $
, then it would be false that
$\alpha =\beta $
, then it would be false that
![]() $\exists n \forall \gamma \in n A(\gamma ,\beta )$
. The point is that our initial motivation for
$\exists n \forall \gamma \in n A(\gamma ,\beta )$
. The point is that our initial motivation for
![]() $LS3$
relied on the idea that A must hold on the basis of some finite portion of
$LS3$
relied on the idea that A must hold on the basis of some finite portion of
![]() $\alpha $
’s graph. But
$\alpha $
’s graph. But
![]() $\alpha =\beta $
would provide some information about the entirety of
$\alpha =\beta $
would provide some information about the entirety of
![]() $\alpha $
’s future graph, namely that it coincides with
$\alpha $
’s future graph, namely that it coincides with
![]() $\beta $
’s graph. Thus we want to rule out this extra bit of information.
$\beta $
’s graph. Thus we want to rule out this extra bit of information.
Now in fact, we can require that the
![]() $\beta $
’s also be pairwise distinct. Since identity is decidable,
$\beta $
’s also be pairwise distinct. Since identity is decidable,
![]() $A(\alpha ,\beta _1,\beta _2)$
is equivalent to
$A(\alpha ,\beta _1,\beta _2)$
is equivalent to
![]() $[A(\alpha ,\beta _1,\beta _2) \wedge \beta _1\neq \beta _2 ] \vee [A(\alpha ,\beta _1,\beta _1)\wedge \beta _1=\beta _2]$
. The generalization to more than two variables
$[A(\alpha ,\beta _1,\beta _2) \wedge \beta _1\neq \beta _2 ] \vee [A(\alpha ,\beta _1,\beta _1)\wedge \beta _1=\beta _2]$
. The generalization to more than two variables
![]() $\beta _i$
is obvious. This gives the following alternative formulation of
$\beta _i$
is obvious. This gives the following alternative formulation of
![]() $LS3$
which it will be somewhat more convenient to work with when we interpret
$LS3$
which it will be somewhat more convenient to work with when we interpret
![]() $LS$
in
$LS$
in
![]() $MC_{LS}$
.Footnote
14
$MC_{LS}$
.Footnote
14
-
LS3′

Finally, it is easy to observe that this axiom justifies the principle of
![]() $\forall \alpha \exists x$
-continuity (also called weak continuity for numbers):
$\forall \alpha \exists x$
-continuity (also called weak continuity for numbers):
To obtain this schema from
![]() $LS3$
, for each
$LS3$
, for each
![]() $\alpha $
and x satisfying
$\alpha $
and x satisfying
![]() $ A(\alpha ,x)$
we find an n as in
$ A(\alpha ,x)$
we find an n as in
![]() $LS3$
(i.e.,
$LS3$
(i.e.,
![]() $\forall \gamma \in n A(\gamma ,x)$
). Then trivially there is a y such that
$\forall \gamma \in n A(\gamma ,x)$
). Then trivially there is a y such that
![]() $\overline {\alpha }(y)=n$
, so we have
$\overline {\alpha }(y)=n$
, so we have
Then some easy quantificational logic gives us the principle of
![]() $\forall \alpha \exists x$
-continuity.
$\forall \alpha \exists x$
-continuity.
The fourth and final axiom is also a continuity principle, saying roughly that whenever a lawlike sequence can be chosen from a lawless sequence, then there is a uniform, lawlike way of choosing each such lawlike sequence on the basis of the neighborhood in which each lawless sequence is found.
The precise statement of this fourth axiom is more technical, and requires the notion of a neighborhood function. If
![]() $F \subset \mathbb {N}^{\mathbb {N}}$
is a class of mappings on natural numbers, a neighborhood function on F encodes a continuous functional
$F \subset \mathbb {N}^{\mathbb {N}}$
is a class of mappings on natural numbers, a neighborhood function on F encodes a continuous functional
![]() $F\rightarrow \mathbb {N}$
. For instance, F might be the classical functions or, in the case that interests us, F will be the lawless sequences. Intuitively, letting
$F\rightarrow \mathbb {N}$
. For instance, F might be the classical functions or, in the case that interests us, F will be the lawless sequences. Intuitively, letting
![]() $K_F$
be the class of neighborhood functions on F, a particular function
$K_F$
be the class of neighborhood functions on F, a particular function
![]() $e\in K_F$
takes initial segments of a sequence
$e\in K_F$
takes initial segments of a sequence
![]() $\xi \in F$
, and
$\xi \in F$
, and
![]() $e(\overline {\xi }(x))=0$
if the initial segment
$e(\overline {\xi }(x))=0$
if the initial segment
![]() $\overline {\xi }(x)$
is not long enough to determine the value of the function that e encodes and
$\overline {\xi }(x)$
is not long enough to determine the value of the function that e encodes and
![]() $e(\overline {\xi }(x))=y+1$
if the function that e codes takes value y on any argument that agrees with
$e(\overline {\xi }(x))=y+1$
if the function that e codes takes value y on any argument that agrees with
![]() $\xi $
on the first x arguments. The class of neighborhood functions on lawless sequences can be defined as the class of e satisfying:
$\xi $
on the first x arguments. The class of neighborhood functions on lawless sequences can be defined as the class of e satisfying:
Let
![]() $e\in K_0$
abbreviate this formula. For brevity, define
$e\in K_0$
abbreviate this formula. For brevity, define
![]() $e(\alpha )=x :\leftrightarrow \exists y (e(\overline {\alpha }(y)=x+1)$
. Finally, let
$e(\alpha )=x :\leftrightarrow \exists y (e(\overline {\alpha }(y)=x+1)$
. Finally, let
![]() $\nu _p (\alpha _1,\dots ,\alpha _p):=\lambda x.\nu _p (\alpha _1(x),\dots ,\alpha _p(x))$
be a pairing function on sequences.
$\nu _p (\alpha _1,\dots ,\alpha _p):=\lambda x.\nu _p (\alpha _1(x),\dots ,\alpha _p(x))$
be a pairing function on sequences.
If e is a neighborhood function on lawless sequences, then it is reasonable also to see e as a neighborhood function encoding a continuous functional
![]() $F\rightarrow \mathbb {N}$
for any class of functions
$F\rightarrow \mathbb {N}$
for any class of functions
![]() $F\subseteq \mathbb {N}^{\mathbb {N}}$
. If you simply abstract away from any intensional information you have about
$F\subseteq \mathbb {N}^{\mathbb {N}}$
. If you simply abstract away from any intensional information you have about
![]() $f\in F$
, then you can treat its graph as though it were the graph of a lawless function, and scan through that graph until you find an n such that
$f\in F$
, then you can treat its graph as though it were the graph of a lawless function, and scan through that graph until you find an n such that
![]() $e(\overline {f}(n))>0$
. This idea that any neighborhood function on lawless sequences induces a neighborhood function on all functions
$e(\overline {f}(n))>0$
. This idea that any neighborhood function on lawless sequences induces a neighborhood function on all functions
![]() $\mathbb {N}^{\mathbb {N}}$
is the so-called extension principle.
$\mathbb {N}^{\mathbb {N}}$
is the so-called extension principle.
Now,
![]() $\nu _p (\alpha _1,\dots ,\alpha _p)\in \mathbb {N}^{\mathbb {N}}$
, so we should also be able to regard any
$\nu _p (\alpha _1,\dots ,\alpha _p)\in \mathbb {N}^{\mathbb {N}}$
, so we should also be able to regard any
![]() $e\in K_0$
as a neighborhood function for p-tuples of lawless sequences as well. This leads to the following preliminary version of
$e\in K_0$
as a neighborhood function for p-tuples of lawless sequences as well. This leads to the following preliminary version of
![]() $LS4$
.
$LS4$
.
-
LS40

The motivation for this is similar to
![]() $LS3$
: if for any lawless sequence you can find a lawlike sequence satisfying A, then this must be possible on the basis of some initial data from the lawless sequence. So for some neighborhood there is a lawlike way of finding the lawlike sequence from the value of the neighborhood function on that lawless sequence. Then we can extend this idea to multiple lawless sequences by taking them together via pairing as a single sequence. Since this sequence of p-tuples was formed by pairing sequences that are entirely lawless, the paired sequence should not exhibit any lawlike behavior either. Just as we were able to use a neighborhood function to find a lawlike sequence from a single lawless sequence, we should be able to do similarly with a p-tuple of lawless sequences. Hence Troelstra’s gloss on this axiom is that “with respect to operations of types
$LS3$
: if for any lawless sequence you can find a lawlike sequence satisfying A, then this must be possible on the basis of some initial data from the lawless sequence. So for some neighborhood there is a lawlike way of finding the lawlike sequence from the value of the neighborhood function on that lawless sequence. Then we can extend this idea to multiple lawless sequences by taking them together via pairing as a single sequence. Since this sequence of p-tuples was formed by pairing sequences that are entirely lawless, the paired sequence should not exhibit any lawlike behavior either. Just as we were able to use a neighborhood function to find a lawlike sequence from a single lawless sequence, we should be able to do similarly with a p-tuple of lawless sequences. Hence Troelstra’s gloss on this axiom is that “with respect to operations of types
![]() $\mathbb {N}^{\mathbb {N}}\rightarrow \mathbb {N}$
, p-tuples of independent lawless sequences behave like single lawless sequences” ([Reference Troelstra31, p. 28]).
$\mathbb {N}^{\mathbb {N}}\rightarrow \mathbb {N}$
, p-tuples of independent lawless sequences behave like single lawless sequences” ([Reference Troelstra31, p. 28]).
To get from this preliminary version
![]() $LS4_0$
to the final, official axiom
$LS4_0$
to the final, official axiom
![]() $LS4$
, we need to introduce another class of functions, denoted K. K is inductively defined as the least class of functions satisfying the following two conditions:
$LS4$
, we need to introduce another class of functions, denoted K. K is inductively defined as the least class of functions satisfying the following two conditions:
-
K1
 $\exists y>0 \forall x f(x)=y \rightarrow f\in K$
.
$\exists y>0 \forall x f(x)=y \rightarrow f\in K$
. -
K2
 $[f(0)=0 \wedge \forall x \exists g\in K (\forall n\in Seq \, f(\langle x \rangle ^\frown n)=g(n))] \rightarrow f\in K$
.
$[f(0)=0 \wedge \forall x \exists g\in K (\forall n\in Seq \, f(\langle x \rangle ^\frown n)=g(n))] \rightarrow f\in K$
.
It is plausible that
![]() $K=K_0$
. It is easy to check that
$K=K_0$
. It is easy to check that
![]() $K_0$
satisfies both K1 and K2, so that
$K_0$
satisfies both K1 and K2, so that
![]() $K_0\subseteq K$
. Conversely, let
$K_0\subseteq K$
. Conversely, let
![]() $e\in K_0$
be arbitrary. Then the tree of n such that
$e\in K_0$
be arbitrary. Then the tree of n such that
![]() $e(n)=0$
will be well-founded, and we can argue by transfinite induction that for every node n in this tree,
$e(n)=0$
will be well-founded, and we can argue by transfinite induction that for every node n in this tree,
![]() $\lambda m. e(n^\frown m)\in K$
, and hence
$\lambda m. e(n^\frown m)\in K$
, and hence
![]() $\lambda m. e(\langle \rangle ^\frown m):= e\in K$
. This argument can be fleshed out into a formally rigorous argument (as we will see in Theorem 8.19), though the inclusion
$\lambda m. e(\langle \rangle ^\frown m):= e\in K$
. This argument can be fleshed out into a formally rigorous argument (as we will see in Theorem 8.19), though the inclusion
![]() $K_0\subseteq K$
requires application of the law of excluded middle, and so is non-constructive. Intuitionistically,
$K_0\subseteq K$
requires application of the law of excluded middle, and so is non-constructive. Intuitionistically,
![]() $K=K_0$
can be proved by (decidable) Bar Induction and in fact is equivalent to decidable Bar Induction in the background theory of elementary analysis ([Reference Troelstra and van Dalen34, p. 4.8.13]).
$K=K_0$
can be proved by (decidable) Bar Induction and in fact is equivalent to decidable Bar Induction in the background theory of elementary analysis ([Reference Troelstra and van Dalen34, p. 4.8.13]).
Adopting the identification
![]() $K=K_0$
gives us our final formulation of
$K=K_0$
gives us our final formulation of
![]() $LS4$
.
$LS4$
.
-
LS4

7 The Beth–Kripke translation
The main goal of this paper is to provide an interpretation of the intuitionistic theory
![]() $LS$
in the classical modal theory
$LS$
in the classical modal theory
![]() $MC_{LS}$
. In this section, I introduce the translation that will be used for that interpretation. This translation was defined in [Reference Brauer, Linnebo and Shapiro7], where it was also shown to provide a faithful translation of intuitionistic logic in
$MC_{LS}$
. In this section, I introduce the translation that will be used for that interpretation. This translation was defined in [Reference Brauer, Linnebo and Shapiro7], where it was also shown to provide a faithful translation of intuitionistic logic in
![]() $\mathbf {S4}_{\mathcal {I}}$
. For full details the reader may refer to that paper; I will just sketch the main ideas behind the translation.
$\mathbf {S4}_{\mathcal {I}}$
. For full details the reader may refer to that paper; I will just sketch the main ideas behind the translation.
The translation is inspired by a variant of the familiar Beth semantics for intuitionistic logic, which allows the domains of worlds in the model to grow. Such models are sometimes called Beth–Kripke models, and hence the translation was called the Beth–Kripke translation. One further tweak that [Reference Brauer, Linnebo and Shapiro7] add is to require that for every term in the relevant language, and every path through the Beth–Kripke model, there is a world where that term has a denotation.
The insight that enables our translation is that a Beth–Kripke model for intuitionistic logic can equally be viewed as a model for
![]() $\mathbf {S4}_{\mathcal {I}}$
by using the respective semantic clauses. Moreover, the semantic clauses for intuitionistic forcing can be explicitly mimicked in an
$\mathbf {S4}_{\mathcal {I}}$
by using the respective semantic clauses. Moreover, the semantic clauses for intuitionistic forcing can be explicitly mimicked in an
![]() $\mathbf {S4}_{\mathcal {I}}$
model by adding some modal operators. This is done according to the following translation.
$\mathbf {S4}_{\mathcal {I}}$
model by adding some modal operators. This is done according to the following translation.

When we are working in many-sorted logic, all the quantifiers are translated according to this scheme, no matter what type o is.
Now it is easy to see that for any non-modal formula A,
![]() $T\Vdash A$
as a Beth–Kripke model just in case
$T\Vdash A$
as a Beth–Kripke model just in case
![]() $T\models A^{\mathsf {B}}$
as an
$T\models A^{\mathsf {B}}$
as an
![]() $\mathbf {S4}_{\mathcal {I}}$
model. The last detail to take care of is that in our variant Beth–Kripke models, it is required that each term eventually have a denotation. For a term t, the following condition asserts that t inevitably exists:
$\mathbf {S4}_{\mathcal {I}}$
model. The last detail to take care of is that in our variant Beth–Kripke models, it is required that each term eventually have a denotation. For a term t, the following condition asserts that t inevitably exists:
For a fixed language
![]() $\mathcal {L}$
, let
$\mathcal {L}$
, let
![]() $IE:=\lbrace IE_t : t\in \mathcal {L} \rbrace $
. Then we have the following result, which shows that the deductive system for
$IE:=\lbrace IE_t : t\in \mathcal {L} \rbrace $
. Then we have the following result, which shows that the deductive system for
![]() $\mathbf {S4}_{\mathcal {I}}$
given in Section 4 faithfully interprets intuitionistic logic via the
$\mathbf {S4}_{\mathcal {I}}$
given in Section 4 faithfully interprets intuitionistic logic via the
![]() $\mathsf {B}$
translation.
$\mathsf {B}$
translation.
Theorem 7.1. For every formula A and set of formulas
![]() $\Gamma $
of many-sorted logic,
$\Gamma $
of many-sorted logic,
![]() $\Gamma \vdash _I A$
iff
$\Gamma \vdash _I A$
iff
![]() $IE, \Gamma ^{\mathsf {B}} \vdash _{S4_{\mathcal {I}}} A^{\mathsf {B}}$
.
$IE, \Gamma ^{\mathsf {B}} \vdash _{S4_{\mathcal {I}}} A^{\mathsf {B}}$
.
We have already observed that
![]() $MC_{LS}$
proves that each term eventually denotes. Thus, in order to prove that
$MC_{LS}$
proves that each term eventually denotes. Thus, in order to prove that
![]() $MC_{LS}$
interprets the intuitionistic theory
$MC_{LS}$
interprets the intuitionistic theory
![]() $LS$
it remains to show that
$LS$
it remains to show that
![]() $MC_{LS}$
proves the
$MC_{LS}$
proves the
![]() $\mathsf {B}$
translations of the axioms of
$\mathsf {B}$
translations of the axioms of
![]() $LS$
.
$LS$
.
8 Interpreting
 $LS$
$LS$
In this section I show that
![]() $MC_{LS}$
does indeed interpret
$MC_{LS}$
does indeed interpret
![]() $LS$
under the
$LS$
under the
![]() $\mathsf {B}$
translation. As just noted, it only remains to show that the translations of axioms of
$\mathsf {B}$
translation. As just noted, it only remains to show that the translations of axioms of
![]() $LS$
are provable in
$LS$
are provable in
![]() $MC_{LS}$
. In Section 8.1 I do this for
$MC_{LS}$
. In Section 8.1 I do this for
![]() $LS1$
and
$LS1$
and
![]() $LS2$
, along with noting a few other simple facts. In Section 8.2 I prove the translations of
$LS2$
, along with noting a few other simple facts. In Section 8.2 I prove the translations of
![]() $LS3$
and
$LS3$
and
![]() $LS4$
. The key tool here is an elimination theorem showing that each formula
$LS4$
. The key tool here is an elimination theorem showing that each formula
![]() $A^{\mathsf {B}}$
is equivalent to an arithmetical formula. Then in Section 8.3 I finally note that
$A^{\mathsf {B}}$
is equivalent to an arithmetical formula. Then in Section 8.3 I finally note that
![]() $MC_{LS}$
interprets the base theory of elementary analysis that
$MC_{LS}$
interprets the base theory of elementary analysis that
![]() $LS$
is built on.
$LS$
is built on.
8.1 Basic properties of
 $MC_{LS}$
$MC_{LS}$
In this subsection I collect some useful simple facts about
![]() $MC_{LS}$
and prove the translations of
$MC_{LS}$
and prove the translations of
![]() $LS1$
and
$LS1$
and
![]() $LS2$
.
$LS2$
.
Lemma 8.1. For every atom
![]() $P(\vec {\alpha },\vec {x},\vec {f})$
,
$P(\vec {\alpha },\vec {x},\vec {f})$
,
![]() $MC_{LS} \vdash \square \forall \vec {\alpha }\forall \vec {x} \forall \vec {f}( P(\vec {\alpha },\vec {x},\vec {f}) \rightarrow \square P(\vec {\alpha },\vec {x},\vec {f}))$
.
$MC_{LS} \vdash \square \forall \vec {\alpha }\forall \vec {x} \forall \vec {f}( P(\vec {\alpha },\vec {x},\vec {f}) \rightarrow \square P(\vec {\alpha },\vec {x},\vec {f}))$
.
Proof The positive stability of identity follows from logic. It is easy to prove
![]() $\forall x \square x=x$
, from which we can infer
$\forall x \square x=x$
, from which we can infer
![]() $t_1=t_1\rightarrow \square t_1=t_1$
using M0.1. Then we infer
$t_1=t_1\rightarrow \square t_1=t_1$
using M0.1. Then we infer
![]() $t_1=t_2 \rightarrow (t_1=t_2\rightarrow \square t_1=t_2)$
using M0.8, which simplifies to
$t_1=t_2 \rightarrow (t_1=t_2\rightarrow \square t_1=t_2)$
using M0.8, which simplifies to
![]() $t_1=t_2\rightarrow \square t_1=t_2$
.
$t_1=t_2\rightarrow \square t_1=t_2$
.
Now suppose P is of the form
![]() $t_1< t_2$
. This is equivalent to
$t_1< t_2$
. This is equivalent to
![]() $\exists x \exists y(t_1=x \wedge t_2 = y \wedge x<y)$
. Then because identity is positively stable we have
$\exists x \exists y(t_1=x \wedge t_2 = y \wedge x<y)$
. Then because identity is positively stable we have
![]() $\square t_1=x$
and
$\square t_1=x$
and
![]() $\square t_2=y$
, and by the stability of
$\square t_2=y$
, and by the stability of
![]() $\mathcal {L}_0$
formulas we have
$\mathcal {L}_0$
formulas we have
![]() $\square x<y$
. All this gives us
$\square x<y$
. All this gives us
![]() $\square t_1<t_2$
.
$\square t_1<t_2$
.
Lemma 8.2. For every
![]() $\mathcal {L}_0$
formula A,
$\mathcal {L}_0$
formula A,
![]() $MC_{LS}\vdash \square ( A \leftrightarrow A^{\mathsf {B}})$
.
$MC_{LS}\vdash \square ( A \leftrightarrow A^{\mathsf {B}})$
.
Proof This follows from the stability of
![]() $\mathcal {L}_0$
formulas by an easy induction on complexity.
$\mathcal {L}_0$
formulas by an easy induction on complexity.
Lemma 8.3.
![]() $MC_{LS}\vdash \square \forall \alpha \forall n \square (\alpha \in n \leftrightarrow (\alpha \in n)^{\mathsf {B}}).$
$MC_{LS}\vdash \square \forall \alpha \forall n \square (\alpha \in n \leftrightarrow (\alpha \in n)^{\mathsf {B}}).$
Proof Reason informally in
![]() $MC_{LS}$
. Assume
$MC_{LS}$
. Assume
![]() $\alpha \in n $
; we want to show
$\alpha \in n $
; we want to show
![]() $(\alpha \in n )^{\mathsf {B}}$
. Now,
$(\alpha \in n )^{\mathsf {B}}$
. Now,
![]() $\alpha \in n$
is an abbreviation of
$\alpha \in n$
is an abbreviation of
![]() $n \in Seq \wedge \forall x(x< lh(n)\rightarrow \alpha (x)=(n)_x)$
, so
$n \in Seq \wedge \forall x(x< lh(n)\rightarrow \alpha (x)=(n)_x)$
, so
![]() $(\alpha \in n )^{\mathsf {B}}$
is
$(\alpha \in n )^{\mathsf {B}}$
is
![]() $( n\in Seq)^{\mathsf {B}} \wedge \square \forall x \square (\mathcal {I}\square x< lh(n) \rightarrow \mathcal {I}\square \alpha (x)=(n)_x)$
. By Lemma 8.2 we get
$( n\in Seq)^{\mathsf {B}} \wedge \square \forall x \square (\mathcal {I}\square x< lh(n) \rightarrow \mathcal {I}\square \alpha (x)=(n)_x)$
. By Lemma 8.2 we get
![]() $(n \in Seq) ^{\mathsf {B}}$
from the assumption that
$(n \in Seq) ^{\mathsf {B}}$
from the assumption that
![]() $n \in Seq $
. Now for arbitrary x, assume
$n \in Seq $
. Now for arbitrary x, assume
![]() $\mathcal {I}\square x< lh(n)$
, and we want to show
$\mathcal {I}\square x< lh(n)$
, and we want to show
![]() $\mathcal {I}\square \alpha (x)=(n)_x$
. Clearly
$\mathcal {I}\square \alpha (x)=(n)_x$
. Clearly
![]() $\mathcal {I}\square x< lh(n)\rightarrow x < lh (n)$
, and from
$\mathcal {I}\square x< lh(n)\rightarrow x < lh (n)$
, and from
![]() $x< lh(n)$
we get
$x< lh(n)$
we get
![]() $\alpha (x)=(n)_x$
. By S3, this then gives
$\alpha (x)=(n)_x$
. By S3, this then gives
![]() $\mathcal {I}\square (\alpha (x)=(n)_x$
as required.
$\mathcal {I}\square (\alpha (x)=(n)_x$
as required.
Conversely, assume
![]() $\neg \alpha \in n$
. Then there is some
$\neg \alpha \in n$
. Then there is some
![]() $m\leq lh(n)$
such that either
$m\leq lh(n)$
such that either
![]() $\alpha (m)$
is undefined or
$\alpha (m)$
is undefined or
![]() $\alpha (m)=t \neq (n)_m$
. In either case,
$\alpha (m)=t \neq (n)_m$
. In either case,
![]() $\lozenge \square \alpha (m)\neq (n)_m$
, which entails
$\lozenge \square \alpha (m)\neq (n)_m$
, which entails
![]() $\neg (\alpha \in n)^{\mathsf {B}}$
.
$\neg (\alpha \in n)^{\mathsf {B}}$
.
Theorem 8.4.
![]() $MC_{LS}\vdash LS1^{\mathsf {B}}$
.
$MC_{LS}\vdash LS1^{\mathsf {B}}$
.
Proof
![]() $LS1^{\mathsf {B}}$
is
$LS1^{\mathsf {B}}$
is
![]() $\square \forall n\in Seq \mathcal {I} \exists \alpha (\alpha \in n)^{\mathsf {B}} $
. Axiom S6 is
$\square \forall n\in Seq \mathcal {I} \exists \alpha (\alpha \in n)^{\mathsf {B}} $
. Axiom S6 is
![]() $\square \forall n\in Seq \mathcal {I} \exists \alpha (\alpha \in n) $
, and by Lemma 8.3 this gives us
$\square \forall n\in Seq \mathcal {I} \exists \alpha (\alpha \in n) $
, and by Lemma 8.3 this gives us
![]() $\square \forall n\in Seq \mathcal {I} \exists \alpha (\alpha \in Seq)^{\mathsf {B}} $
, as required.
$\square \forall n\in Seq \mathcal {I} \exists \alpha (\alpha \in Seq)^{\mathsf {B}} $
, as required.
Now we can approach
![]() $LS2$
in a somewhat similar manner.
$LS2$
in a somewhat similar manner.
Lemma 8.5.
![]() $MC_{LS} \vdash \neg \square \forall x \alpha (x) \simeq \beta (x) \leftrightarrow (\neg \forall x \alpha (x)=\beta (x))^{\mathsf {B}}$
.
$MC_{LS} \vdash \neg \square \forall x \alpha (x) \simeq \beta (x) \leftrightarrow (\neg \forall x \alpha (x)=\beta (x))^{\mathsf {B}}$
.
Proof Note that
![]() $(\neg \forall x \alpha (x)=\beta (x))^{\mathsf {B}}$
is
$(\neg \forall x \alpha (x)=\beta (x))^{\mathsf {B}}$
is
![]() $\square \neg \square \forall x \mathcal {I}\square \alpha (x)=\beta (x)$
. Again, we reason informally within
$\square \neg \square \forall x \mathcal {I}\square \alpha (x)=\beta (x)$
. Again, we reason informally within
![]() $MC_{LS}$
.
$MC_{LS}$
.
First assume
![]() $\neg \square \forall x \alpha (x) \simeq \beta (x)$
. Then by S9 we have
$\neg \square \forall x \alpha (x) \simeq \beta (x)$
. Then by S9 we have
![]() $\lozenge \exists x \exists y \exists z (\alpha (x)=y\neq z = \beta (x))$
, and hence
$\lozenge \exists x \exists y \exists z (\alpha (x)=y\neq z = \beta (x))$
, and hence
![]() $\lozenge \exists x \neg \mathcal {I} \square \alpha (x)=\beta (x)$
. And since by S7
$\lozenge \exists x \neg \mathcal {I} \square \alpha (x)=\beta (x)$
. And since by S7
![]() $\neg \square \forall x \alpha (x)=\beta (x)$
has to hold necessarily, we can infer
$\neg \square \forall x \alpha (x)=\beta (x)$
has to hold necessarily, we can infer
![]() $\square \lozenge \exists x \neg \mathcal {I} \square \alpha (x)=\beta (x)$
, which is equivalent to
$\square \lozenge \exists x \neg \mathcal {I} \square \alpha (x)=\beta (x)$
, which is equivalent to
![]() $(\neg \forall x \alpha (x)=\beta (x))^{\mathsf {B}}$
.
$(\neg \forall x \alpha (x)=\beta (x))^{\mathsf {B}}$
.
Conversely, assume
![]() $\square \forall x(\alpha (x) \simeq \beta (x))$
. Since we know
$\square \forall x(\alpha (x) \simeq \beta (x))$
. Since we know
![]() $\square \forall x \mathcal {I}\alpha (x)=\alpha (x)$
, it follows that
$\square \forall x \mathcal {I}\alpha (x)=\alpha (x)$
, it follows that
![]() $\square \forall x \mathcal {I}\alpha (x)=\beta (x)$
. And since identity is positively stable, we get
$\square \forall x \mathcal {I}\alpha (x)=\beta (x)$
. And since identity is positively stable, we get
![]() $\square \forall x \mathcal {I}\square \alpha (x)=\beta (x)$
. Hence
$\square \forall x \mathcal {I}\square \alpha (x)=\beta (x)$
. Hence
![]() $\lozenge \square \forall x \mathcal {I}\square \alpha (x)=\beta (x)$
, which is equivalent to
$\lozenge \square \forall x \mathcal {I}\square \alpha (x)=\beta (x)$
, which is equivalent to
![]() $\neg (\neg \forall x \alpha (x)=\beta (x))^{\mathsf {B}}$
.
$\neg (\neg \forall x \alpha (x)=\beta (x))^{\mathsf {B}}$
.
Theorem 8.6.
![]() $MC_{LS}\vdash LS2^{\mathsf {B}}$
.
$MC_{LS}\vdash LS2^{\mathsf {B}}$
.
Proof
![]() $LS2$
is
$LS2$
is
![]() $\alpha =\beta \vee \neg \alpha =\beta $
, and recall that
$\alpha =\beta \vee \neg \alpha =\beta $
, and recall that
![]() $\alpha =\beta $
is an abbreviation for
$\alpha =\beta $
is an abbreviation for
![]() $\forall x(\alpha (x)=\beta (x))$
. So
$\forall x(\alpha (x)=\beta (x))$
. So
![]() $LS2^{\mathsf {B}}$
is
$LS2^{\mathsf {B}}$
is
![]() $\mathcal {I}[\square \forall x \mathcal {I}\square (\alpha (x)=\beta (x))\vee \square \neg \square \forall x\mathcal {I} \square (\alpha (x)=\beta (x))]$
. Since our theory is classical, we know that either
$\mathcal {I}[\square \forall x \mathcal {I}\square (\alpha (x)=\beta (x))\vee \square \neg \square \forall x\mathcal {I} \square (\alpha (x)=\beta (x))]$
. Since our theory is classical, we know that either
![]() $\square \forall x \alpha (x)\simeq \beta (x)$
or
$\square \forall x \alpha (x)\simeq \beta (x)$
or
![]() $\neg \square \forall x \alpha (x)\simeq \beta (x)$
.
$\neg \square \forall x \alpha (x)\simeq \beta (x)$
.
In the first case, it follows as in the previous lemma that
![]() $\square \forall x \mathcal {I}\square \alpha (x)=\beta (x)$
, i.e.,
$\square \forall x \mathcal {I}\square \alpha (x)=\beta (x)$
, i.e.,
![]() $(\alpha =\beta )^{\mathsf {B}}$
. In the second case, Lemma 8.5 gives us
$(\alpha =\beta )^{\mathsf {B}}$
. In the second case, Lemma 8.5 gives us
![]() $(\neg \forall x \alpha (x)=\beta (x))^{\mathsf {B}}$
.
$(\neg \forall x \alpha (x)=\beta (x))^{\mathsf {B}}$
.
Thus we have
![]() $(\alpha (x)=\beta (x))^{\mathsf {B}} \vee (\alpha (x)\neq \beta (x))^{\mathsf {B}}$
and hence
$(\alpha (x)=\beta (x))^{\mathsf {B}} \vee (\alpha (x)\neq \beta (x))^{\mathsf {B}}$
and hence
![]() $\mathcal {I}[(\alpha (x)=\beta (x))^{\mathsf {B}} \vee (\alpha (x)\neq \beta (x))^{\mathsf {B}}]$
.
$\mathcal {I}[(\alpha (x)=\beta (x))^{\mathsf {B}} \vee (\alpha (x)\neq \beta (x))^{\mathsf {B}}]$
.
I close this section with one more basic fact.
Proposition 8.7. For any formula A,
![]() $MC_{LS}\vdash \square \forall x \alpha (x) \simeq \beta (x) \rightarrow (A\alpha \leftrightarrow A\beta ) $
.
$MC_{LS}\vdash \square \forall x \alpha (x) \simeq \beta (x) \rightarrow (A\alpha \leftrightarrow A\beta ) $
.
Proof Induction on the complexity of A. For the basis step, A is an atom of the form
![]() $t_1 = t_2$
or
$t_1 = t_2$
or
![]() $t_1 \leq t_2$
. We can do a subsidiary induction on the complexity of
$t_1 \leq t_2$
. We can do a subsidiary induction on the complexity of
![]() $t_1$
and
$t_1$
and
![]() $t_2$
, which is in turn entirely straightforward.
$t_2$
, which is in turn entirely straightforward.
For the induction step, when the main connective in A is truth-functional (that is, not a modal operator), the claim follows easily from the i.h.
When the main connective in A is a modal operator, first note that the i.h. gives us a proof of
![]() $ \square \forall x \alpha (x) \simeq \beta (x) \rightarrow \square (B\alpha \leftrightarrow B\beta ) $
. Now from
$ \square \forall x \alpha (x) \simeq \beta (x) \rightarrow \square (B\alpha \leftrightarrow B\beta ) $
. Now from
![]() $\square (B\alpha \leftrightarrow B\beta )$
we can easily infer each of
$\square (B\alpha \leftrightarrow B\beta )$
we can easily infer each of
![]() $\square B\alpha \leftrightarrow \square B\beta $
,
$\square B\alpha \leftrightarrow \square B\beta $
,
![]() $\lozenge B\alpha \leftrightarrow \lozenge B\beta $
, and
$\lozenge B\alpha \leftrightarrow \lozenge B\beta $
, and
![]() $\mathcal {I} B\alpha \leftrightarrow \mathcal {I} B\beta $
, giving the desired result.
$\mathcal {I} B\alpha \leftrightarrow \mathcal {I} B\beta $
, giving the desired result.
8.2 Continuity principles
In this section I show that
![]() $MC_{LS}$
proves
$MC_{LS}$
proves
![]() $LS3^{\mathsf {B}}$
and
$LS3^{\mathsf {B}}$
and
![]() $LS4^{\mathsf {B}}$
. To do so, I will establish an elimination theorem showing that every formula A in the range of the
$LS4^{\mathsf {B}}$
. To do so, I will establish an elimination theorem showing that every formula A in the range of the
![]() $\mathsf {B}$
translation is equivalent to an arithmetical formula with no occurrences of choice sequence variables, either free or bound.Footnote
15
When A is in the range of the
$\mathsf {B}$
translation is equivalent to an arithmetical formula with no occurrences of choice sequence variables, either free or bound.Footnote
15
When A is in the range of the
![]() $\mathsf {B}$
translation, we can define the arithmetical translation T of A relative to
$\mathsf {B}$
translation, we can define the arithmetical translation T of A relative to
![]() $\vec {n}$
. If A has k choice sequence parameters,
$\vec {n}$
. If A has k choice sequence parameters,
![]() $T(A,\vec {n})$
will be an arithmetical formula with k number parameters
$T(A,\vec {n})$
will be an arithmetical formula with k number parameters
![]() $n_1,\dots ,n_k$
. The intention is that when A says something about
$n_1,\dots ,n_k$
. The intention is that when A says something about
![]() $\alpha _1,\dots ,\alpha _k$
,
$\alpha _1,\dots ,\alpha _k$
,
![]() $T(A,\vec {n})$
says something about all classical functions
$T(A,\vec {n})$
says something about all classical functions
![]() $g_1,\dots ,g_k$
that have initial segments
$g_1,\dots ,g_k$
that have initial segments
![]() $n_1,\dots ,n_k$
. The elimination theorem will then show that these are equivalent, so that any formula
$n_1,\dots ,n_k$
. The elimination theorem will then show that these are equivalent, so that any formula
![]() $A^{\mathsf {B}}(\alpha )$
amounts to a claim that all classical functions with
$A^{\mathsf {B}}(\alpha )$
amounts to a claim that all classical functions with
![]() $\mathrm {is} \alpha $
as an initial segment behave in a certain way.
$\mathrm {is} \alpha $
as an initial segment behave in a certain way.
Definition 8.8 (T-translation).
If A is a formula in the range of the
![]() $\mathsf {B}$
translation with at most k choice sequence parameters
$\mathsf {B}$
translation with at most k choice sequence parameters
![]() $\alpha _1,\dots ,\alpha _k$
, define the translation
$\alpha _1,\dots ,\alpha _k$
, define the translation
![]() $T(A,\vec {n})$
relative to sequence numbers
$T(A,\vec {n})$
relative to sequence numbers
![]() $n_1,\dots ,n_k$
inductively as follows:
$n_1,\dots ,n_k$
inductively as follows:
-
• When A is the translation of an atom,
 $\mathcal {I}\square P(\vec {x},\vec {\alpha },\vec {f})$
, define
$\mathcal {I}\square P(\vec {x},\vec {\alpha },\vec {f})$
, define
 $T(A,\vec {n})$
to be
$T(A,\vec {n})$
to be  $$ \begin{align*}\forall g_1\in n_1 \dots \forall g_k\in n_k \exists y_1\dots\exists y_k \forall h_1\in \overline{g_1}(y_1) \dots \forall h_k \in \overline{g_k}(y_k) P(\vec{x},\vec{h},\vec{f}).\end{align*} $$
$$ \begin{align*}\forall g_1\in n_1 \dots \forall g_k\in n_k \exists y_1\dots\exists y_k \forall h_1\in \overline{g_1}(y_1) \dots \forall h_k \in \overline{g_k}(y_k) P(\vec{x},\vec{h},\vec{f}).\end{align*} $$
-
• When A is a conjunction
 $B \wedge C$
, let
$B \wedge C$
, let
 $T(A,\vec {n})$
be
$T(A,\vec {n})$
be
 $T(B,\vec {n})\wedge T(C,\vec {n})$
.
$T(B,\vec {n})\wedge T(C,\vec {n})$
. -
• When A is
 $\mathcal {I}(B \vee C)$
, let
$\mathcal {I}(B \vee C)$
, let
 $T(A,\vec {n})$
be
$T(A,\vec {n})$
be
 $\forall \vec {g}\in \vec {n}\exists \vec {y} \left ( T\left ( B,\overrightarrow {\overline {g}(y)} \right ) \vee T \left ( C,\overrightarrow {\overline {g}(y)}\right ) \right )$
.
$\forall \vec {g}\in \vec {n}\exists \vec {y} \left ( T\left ( B,\overrightarrow {\overline {g}(y)} \right ) \vee T \left ( C,\overrightarrow {\overline {g}(y)}\right ) \right )$
. -
• When A is
 $\square \neg B$
, let
$\square \neg B$
, let
 $T(A,\vec {n})$
be
$T(A,\vec {n})$
be
 $\forall \vec {m} \succeq \vec {n} \neg T(B,\vec {m})$
.
$\forall \vec {m} \succeq \vec {n} \neg T(B,\vec {m})$
. -
• When A is
 $\square (B \rightarrow C)$
, let
$\square (B \rightarrow C)$
, let
 $T(A,a)$
be
$T(A,a)$
be
 $\forall \vec {m} \succeq \vec {n} \big ( T(B,\vec {m}) \rightarrow T(C,\vec {m}) \big )$
.
$\forall \vec {m} \succeq \vec {n} \big ( T(B,\vec {m}) \rightarrow T(C,\vec {m}) \big )$
. -
• When A is
 $\square \forall x B$
, let
$\square \forall x B$
, let
 $T(A,\vec {n})$
be
$T(A,\vec {n})$
be
 $\forall \vec {m}\succeq \vec {n} \forall x T(B,\vec {m})$
.
$\forall \vec {m}\succeq \vec {n} \forall x T(B,\vec {m})$
. -
• When A is
 $\square \forall f B$
, let
$\square \forall f B$
, let
 $T(A,\vec {n})$
be
$T(A,\vec {n})$
be
 $\forall \vec {m}\succeq \vec {n} \forall f T(B,\vec {m})$
.
$\forall \vec {m}\succeq \vec {n} \forall f T(B,\vec {m})$
. -
• When A is
 $\mathcal {I} \exists x B$
, let
$\mathcal {I} \exists x B$
, let
 $T(A,\vec {n})$
be
$T(A,\vec {n})$
be
 $\forall \vec {g}\in \vec {n} \exists \vec {y} \exists x T\left (B,\overrightarrow {\overline {g}(y)}\right )$
.
$\forall \vec {g}\in \vec {n} \exists \vec {y} \exists x T\left (B,\overrightarrow {\overline {g}(y)}\right )$
. -
• When A is
 $\mathcal {I} \exists f B$
, let
$\mathcal {I} \exists f B$
, let
 $T(A,\vec {n})$
be
$T(A,\vec {n})$
be
 $\forall \vec {g}\in \vec {n} \exists \vec {y} \exists f T\left ( B,\overrightarrow {\overline {g}(y)} \right )$
.
$\forall \vec {g}\in \vec {n} \exists \vec {y} \exists f T\left ( B,\overrightarrow {\overline {g}(y)} \right )$
. -
• When A is
 $\square \forall \alpha _{k+1} B$
, let
$\square \forall \alpha _{k+1} B$
, let
 $T(A,\vec {n})$
be
$T(A,\vec {n})$
be  $$ \begin{align*}\forall \vec{m} \succeq \vec{n} \left( \bigwedge_{1\leq i \leq k} T(B^{\alpha_{k+1}}_{\alpha_i},\vec{m}) \wedge \forall m_{k+1}\in Seq \, T(B,\vec{m}, m_{k+1}) \right).\end{align*} $$
$$ \begin{align*}\forall \vec{m} \succeq \vec{n} \left( \bigwedge_{1\leq i \leq k} T(B^{\alpha_{k+1}}_{\alpha_i},\vec{m}) \wedge \forall m_{k+1}\in Seq \, T(B,\vec{m}, m_{k+1}) \right).\end{align*} $$
-
• When A is
 $\mathcal {I}\exists \alpha _{k+1}B$
, let
$\mathcal {I}\exists \alpha _{k+1}B$
, let
 $T(A,\vec {n})$
be
$T(A,\vec {n})$
be  $$ \begin{align*}\forall \vec{g}\in \vec{n} \exists \vec{y} \left( \bigvee_{1\leq i \leq k} T\left(B^{\alpha_{k+1}}_{\alpha_i},\overrightarrow{\overline{g}(y)} \right) \vee \exists m \in Seq \, T\left(B,\overrightarrow{\overline{g}(y)},m\right) \right).\end{align*} $$
$$ \begin{align*}\forall \vec{g}\in \vec{n} \exists \vec{y} \left( \bigvee_{1\leq i \leq k} T\left(B^{\alpha_{k+1}}_{\alpha_i},\overrightarrow{\overline{g}(y)} \right) \vee \exists m \in Seq \, T\left(B,\overrightarrow{\overline{g}(y)},m\right) \right).\end{align*} $$
The goal will be to show that any formula in the range of the
![]() $\mathsf {B}$
translation is equivalent to its T translation. I begin with some simple facts that I will often appeal to without mention.
$\mathsf {B}$
translation is equivalent to its T translation. I begin with some simple facts that I will often appeal to without mention.
Proposition 8.9. When A is in the range of the
![]() $\mathsf {B}$
translation,
$\mathsf {B}$
translation,
![]() $T(A,\vec {n})$
is a formula in the language
$T(A,\vec {n})$
is a formula in the language
![]() $\mathcal {L}_0$
of second-order arithmetic. Hence
$\mathcal {L}_0$
of second-order arithmetic. Hence
![]() $T(A,\vec {n})$
is positively and negatively stable.
$T(A,\vec {n})$
is positively and negatively stable.
Lemma 8.10. Say
![]() $\vec {x}$
and
$\vec {x}$
and
![]() $\vec {f}$
are the free variables in
$\vec {f}$
are the free variables in
![]() $T(A,m,\vec {n})$
. Then
$T(A,m,\vec {n})$
. Then
![]() $MC_{LS}$
proves:
$MC_{LS}$
proves:
-
1. For all
 $\vec {x}$
and
$\vec {x}$
and
 $\vec {f}$
, if
$\vec {f}$
, if
 $T(A,m,\vec {n})$
and
$T(A,m,\vec {n})$
and
 $m\preceq m'$
, then
$m\preceq m'$
, then
 $T(A,m',\vec {n})$
.
$T(A,m',\vec {n})$
. -
2. For all
 $\vec {x}$
and
$\vec {x}$
and
 $\vec {f}$
, if for all
$\vec {f}$
, if for all
 $m'\succ m$
,
$m'\succ m$
,
 $T(A,m', \vec {n})$
, then
$T(A,m', \vec {n})$
, then
 $T(A,m,\vec {n})$
.
$T(A,m,\vec {n})$
.
Proof Both claims can be proved simultaneously by a straightforward induction on A.
I will also define one more notion, which I will call the
![]() $\alpha $
-n replacement of an atom P. This notion only plays a supporting role in the proof of the elimination theorem, but it will return in Section 9 as a key part of the conservativity argument there.
$\alpha $
-n replacement of an atom P. This notion only plays a supporting role in the proof of the elimination theorem, but it will return in Section 9 as a key part of the conservativity argument there.
Definition 8.11 (
 $\alpha $
-n replacement).
$\alpha $
-n replacement).
Given an atom
![]() $P(\vec {\alpha })$
, possibly with other free variables not shown, define the
$P(\vec {\alpha })$
, possibly with other free variables not shown, define the
![]() $\vec {\alpha }$
-
$\vec {\alpha }$
-
![]() $\vec {n}$
replacement
$\vec {n}$
replacement
![]() $\mathcal {R}(P,\vec {\alpha },\vec {n})$
as follows. Let
$\mathcal {R}(P,\vec {\alpha },\vec {n})$
as follows. Let
![]() $\alpha _{i_1}(t_1),\dots ,\alpha _{i_k}(t_k)$
be a list of all occurrences of choice sequence variables and their arguments, subject to the constraint that no earlier item on the list itself contains an occurrence of an item later in the list. Let
$\alpha _{i_1}(t_1),\dots ,\alpha _{i_k}(t_k)$
be a list of all occurrences of choice sequence variables and their arguments, subject to the constraint that no earlier item on the list itself contains an occurrence of an item later in the list. Let
![]() $t_j'$
be the result of successively replacing in
$t_j'$
be the result of successively replacing in
![]() $t_j$
any occurrences of
$t_j$
any occurrences of
![]() $\alpha _{i_l}(t_l)$
, for
$\alpha _{i_l}(t_l)$
, for
![]() $l<j$
, with
$l<j$
, with
![]() $(n_{i_l})_{t_l'}$
. Let
$(n_{i_l})_{t_l'}$
. Let
![]() $P'$
be the result of successively replacing each occurrence of
$P'$
be the result of successively replacing each occurrence of
![]() $\alpha _{i_j}(t_j)$
with
$\alpha _{i_j}(t_j)$
with
![]() $(n_{i_j})_{t_j'}$
. Then
$(n_{i_j})_{t_j'}$
. Then
![]() $\mathcal {R}(P,\vec {\alpha },\vec {n})$
is the formula:
$\mathcal {R}(P,\vec {\alpha },\vec {n})$
is the formula:
 $$ \begin{align*}\left( \bigwedge_{1\leq j\leq k} t_j'<lh(n_{i_j}) \wedge P' \right) \vee \left( \bigvee_{1\leq j\leq k} t_j'\geq lh(n_{i_j}) \wedge 0=1 \right).\end{align*} $$
$$ \begin{align*}\left( \bigwedge_{1\leq j\leq k} t_j'<lh(n_{i_j}) \wedge P' \right) \vee \left( \bigvee_{1\leq j\leq k} t_j'\geq lh(n_{i_j}) \wedge 0=1 \right).\end{align*} $$
(For classical functions
![]() $\vec {g}$
, the
$\vec {g}$
, the
![]() $\vec {g}$
-
$\vec {g}$
-
![]() $\vec {n}$
replacement
$\vec {n}$
replacement
![]() $\mathcal {R}(P,\vec {g},\vec {n})$
can be defined in exactly the same way.)
$\mathcal {R}(P,\vec {g},\vec {n})$
can be defined in exactly the same way.)
This definition is quite wordy, but the idea is simple: we replace occurrences of
![]() $\alpha (x)$
with
$\alpha (x)$
with
![]() $(n)_x$
, and iterate for nested occurrences such as
$(n)_x$
, and iterate for nested occurrences such as
![]() $\alpha _2(\alpha _1(x))$
. The motivation, of course, is that when n is the initial segment of
$\alpha _2(\alpha _1(x))$
. The motivation, of course, is that when n is the initial segment of
![]() $\alpha $
, this will provide an
$\alpha $
, this will provide an
![]() $\mathcal {L}_0$
formula that is equivalent to the original atom containing choice sequence variables. An example of an
$\mathcal {L}_0$
formula that is equivalent to the original atom containing choice sequence variables. An example of an
![]() $\vec {\alpha }$
-
$\vec {\alpha }$
-
![]() $\vec {n}$
replacement will illustrate the idea.
$\vec {n}$
replacement will illustrate the idea.
Example 8.12. Let
![]() $P:\leftrightarrow \alpha _1(\alpha _2(4))< \alpha _3(\alpha _3(2))$
. Then
$P:\leftrightarrow \alpha _1(\alpha _2(4))< \alpha _3(\alpha _3(2))$
. Then
![]() $\mathcal {R}(P,\alpha _1,\alpha _2,\alpha _3, n_1,n_2,n_3)$
is the formula:
$\mathcal {R}(P,\alpha _1,\alpha _2,\alpha _3, n_1,n_2,n_3)$
is the formula:
 $$ \begin{align*} \left( 4< lh(n_2) \wedge (n_2)_4 <lh(n_1) \wedge 2< lh(n_3) \wedge (n_3)_2 < lh (n_3) \wedge (n_1)_{(n_2)_4} < (n_3)_{(n_3)_2} \right)& \\ \vee \big( \big( 4\geq lh(n_2) \vee (n_2)_4 \geq lh(n_1) \vee 2 \geq lh(n_3) \vee (n_3)_2 \geq lh (n_3) \big) \wedge 0=1 \big).& \end{align*} $$
$$ \begin{align*} \left( 4< lh(n_2) \wedge (n_2)_4 <lh(n_1) \wedge 2< lh(n_3) \wedge (n_3)_2 < lh (n_3) \wedge (n_1)_{(n_2)_4} < (n_3)_{(n_3)_2} \right)& \\ \vee \big( \big( 4\geq lh(n_2) \vee (n_2)_4 \geq lh(n_1) \vee 2 \geq lh(n_3) \vee (n_3)_2 \geq lh (n_3) \big) \wedge 0=1 \big).& \end{align*} $$
It is evident that
![]() $P\alpha $
is provably equivalent to its
$P\alpha $
is provably equivalent to its
![]() $\alpha $
-
$\alpha $
-
![]() $\mathrm {is}\ \alpha $
replacement:
$\mathrm {is}\ \alpha $
replacement:
Proposition 8.13. For each atom P,
![]() $MC_{LS}\vdash \square \forall \vec {\alpha } \forall \vec {n} \big(\kern-1.5pt \bigwedge _i \mathrm {is} \alpha _i=n_i \rightarrow( P\vec {\alpha } \leftrightarrow \mathcal {R}(P,\vec {\alpha },\vec {n}) ) \big)$
.
$MC_{LS}\vdash \square \forall \vec {\alpha } \forall \vec {n} \big(\kern-1.5pt \bigwedge _i \mathrm {is} \alpha _i=n_i \rightarrow( P\vec {\alpha } \leftrightarrow \mathcal {R}(P,\vec {\alpha },\vec {n}) ) \big)$
.
And here is the key theorem.
Theorem 8.14 (Elimination theorem).
If A is a formula in the range of the
![]() $\mathsf {B}$
translation with free variables among
$\mathsf {B}$
translation with free variables among
![]() $\vec {x},\vec {f},\vec {\alpha }$
, then
$\vec {x},\vec {f},\vec {\alpha }$
, then
![]() $MC_{LS}$
proves
$MC_{LS}$
proves
 $$ \begin{align*}\square \forall \vec{x} \forall f \forall \vec{\alpha} &\left( \bigwedge_{i,j} \neg \square \forall x \alpha_i(x)\simeq \alpha_j(x)\right.\\& \quad \left.\rightarrow \left( A(\vec{x},\vec{\alpha},\vec{f}) \leftrightarrow \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i = n_i \rightarrow T(A,\vec{n}) \right) \right) \right).\end{align*} $$
$$ \begin{align*}\square \forall \vec{x} \forall f \forall \vec{\alpha} &\left( \bigwedge_{i,j} \neg \square \forall x \alpha_i(x)\simeq \alpha_j(x)\right.\\& \quad \left.\rightarrow \left( A(\vec{x},\vec{\alpha},\vec{f}) \leftrightarrow \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i = n_i \rightarrow T(A,\vec{n}) \right) \right) \right).\end{align*} $$
This is proved by a lengthy induction on the complexity of A. Although the proof illustrates some key argument patterns used in
![]() $MC_{LS}$
, the details are somewhat tedious, and hence it is relegated to Appendix B. With the elimination theorem in hand, it is straightforward to prove the translation of
$MC_{LS}$
, the details are somewhat tedious, and hence it is relegated to Appendix B. With the elimination theorem in hand, it is straightforward to prove the translation of
![]() $LS3'$
.
$LS3'$
.
Theorem 8.15.
![]() $ MC_{LS} \vdash LS3{^{\prime {\mathsf {B}}}}$
.
$ MC_{LS} \vdash LS3{^{\prime {\mathsf {B}}}}$
.
Proof
![]() $LS3{^{\prime {\mathsf {B}}}}$
is
$LS3{^{\prime {\mathsf {B}}}}$
is
 $$ \begin{align*} &\square \Bigg( \Bigg. \left( A^{\mathsf{B}}(\alpha,\vec{\beta}) \wedge \bigwedge_i (\alpha \neq \beta_i)^{\mathsf{B}} \wedge \bigwedge_{i,j} (\beta_i \neq \beta_j)^{\mathsf{B}} \right) \rightarrow \\& \quad \rightarrow \mathcal{I} \exists n \square \left( Seq^{\mathsf{B}}(n) \wedge (\alpha\in n)^{\mathsf{B}} \wedge \square \forall \gamma \square \left( (\gamma\in n)^{\mathsf{B}} \wedge \bigwedge_i (\gamma\neq \beta_i)^{\mathsf{B}} \rightarrow A^{\mathsf{B}}(\gamma,\vec{\beta}) \right) \right) \Bigg. \Bigg). \end{align*} $$
$$ \begin{align*} &\square \Bigg( \Bigg. \left( A^{\mathsf{B}}(\alpha,\vec{\beta}) \wedge \bigwedge_i (\alpha \neq \beta_i)^{\mathsf{B}} \wedge \bigwedge_{i,j} (\beta_i \neq \beta_j)^{\mathsf{B}} \right) \rightarrow \\& \quad \rightarrow \mathcal{I} \exists n \square \left( Seq^{\mathsf{B}}(n) \wedge (\alpha\in n)^{\mathsf{B}} \wedge \square \forall \gamma \square \left( (\gamma\in n)^{\mathsf{B}} \wedge \bigwedge_i (\gamma\neq \beta_i)^{\mathsf{B}} \rightarrow A^{\mathsf{B}}(\gamma,\vec{\beta}) \right) \right) \Bigg. \Bigg). \end{align*} $$
We can immediately make some obvious simplifications in light of the fact that
![]() $Seq(n)$
and
$Seq(n)$
and
![]() $\alpha \in n$
are equivalent to their
$\alpha \in n$
are equivalent to their
![]() $^{\mathsf {B}}$
translations and
$^{\mathsf {B}}$
translations and
![]() $(\alpha \neq \beta )^{\mathsf {B}}$
is equivalent to
$(\alpha \neq \beta )^{\mathsf {B}}$
is equivalent to
![]() $\neg \square \forall x (\alpha (x)\simeq \beta (x))$
.
$\neg \square \forall x (\alpha (x)\simeq \beta (x))$
.
Suppose that
![]() $A^{\mathsf {B}}(\alpha ,\vec {\beta })$
and that
$A^{\mathsf {B}}(\alpha ,\vec {\beta })$
and that
![]() $\alpha $
and the
$\alpha $
and the
![]() $\beta $
’s are all pairwise distinct. Let n be
$\beta $
’s are all pairwise distinct. Let n be
![]() $\mathrm {is} \alpha $
and let
$\mathrm {is} \alpha $
and let
![]() $\mathrm {is} \beta _i=m_i$
. Then by Theorem 8.14 we have
$\mathrm {is} \beta _i=m_i$
. Then by Theorem 8.14 we have
![]() $T(A^{\mathsf {B}},n,\vec {m})$
. Let
$T(A^{\mathsf {B}},n,\vec {m})$
. Let
![]() $\gamma \in n$
be an arbitrary choice sequence distinct from all the
$\gamma \in n$
be an arbitrary choice sequence distinct from all the
![]() $\beta $
’s. Then necessarily there are some
$\beta $
’s. Then necessarily there are some
![]() $n'\succeq n$
and
$n'\succeq n$
and
![]() $\vec {m'}\succeq \vec {m}$
such that is
$\vec {m'}\succeq \vec {m}$
such that is
![]() $\mathrm {\gamma }=n'$
and
$\mathrm {\gamma }=n'$
and
![]() $\mathrm {is} \beta _i=m_i'$
. But by Lemma 8.10, we know
$\mathrm {is} \beta _i=m_i'$
. But by Lemma 8.10, we know
![]() $T(A^{\mathsf {B}},n',\vec {m'})$
, so by Theorem 8.14 we know
$T(A^{\mathsf {B}},n',\vec {m'})$
, so by Theorem 8.14 we know
![]() $A^{\mathsf {B}}(\gamma ,\vec {\beta })$
.
$A^{\mathsf {B}}(\gamma ,\vec {\beta })$
.
I turn now to the translation of
![]() $LS4$
. First, recall the definition of a neighborhood function:
$LS4$
. First, recall the definition of a neighborhood function:
This concept has an equivalent arithmetical definition, as the following lemma shows.
Lemma 8.16.
 $MC_{LS} \vdash (e\in K_0)^{\mathsf {B}} \leftrightarrow \forall g \exists x \, e(\overline {g}(x))> 0 \wedge \forall n (e(n)> 0 \rightarrow \forall m\succeq n \, e(m)=e(n) )$
.
$MC_{LS} \vdash (e\in K_0)^{\mathsf {B}} \leftrightarrow \forall g \exists x \, e(\overline {g}(x))> 0 \wedge \forall n (e(n)> 0 \rightarrow \forall m\succeq n \, e(m)=e(n) )$
.
Proof Observe that
![]() $(e\in K_0)^{\mathsf {B}}$
is equivalent to
$(e\in K_0)^{\mathsf {B}}$
is equivalent to
![]() $\square \forall \alpha \mathcal {I }\exists x \, e(\overline {\alpha }(x))> 0 \wedge \forall n (e(n)\neq 0 \rightarrow \forall m\succeq n \, e(m)=e(n) )$
. So clearly it will suffice to show within
$\square \forall \alpha \mathcal {I }\exists x \, e(\overline {\alpha }(x))> 0 \wedge \forall n (e(n)\neq 0 \rightarrow \forall m\succeq n \, e(m)=e(n) )$
. So clearly it will suffice to show within
![]() $MC_{LS}$
that
$MC_{LS}$
that
![]() $\square \forall \alpha \mathcal {I }\exists x e(\overline {\alpha }(x))> 0 \leftrightarrow \forall g \exists x \, e(\overline {g}(x))>0$
.
$\square \forall \alpha \mathcal {I }\exists x e(\overline {\alpha }(x))> 0 \leftrightarrow \forall g \exists x \, e(\overline {g}(x))>0$
.
First assume
![]() $\square \forall \alpha \mathcal {I} \exists x \, e(\overline {\alpha }(x))> 0$
. Then, in particular, for a sequence
$\square \forall \alpha \mathcal {I} \exists x \, e(\overline {\alpha }(x))> 0$
. Then, in particular, for a sequence
![]() $\gamma $
such that
$\gamma $
such that
![]() $\mathrm {is} \gamma =\langle \rangle $
, it is true that
$\mathrm {is} \gamma =\langle \rangle $
, it is true that
![]() $\mathcal {I}\exists x \, e(\overline {\gamma }(x))>0$
. Every function g agrees with the defined segment of
$\mathcal {I}\exists x \, e(\overline {\gamma }(x))>0$
. Every function g agrees with the defined segment of
![]() $\gamma $
, so for each g it is not inevitable that
$\gamma $
, so for each g it is not inevitable that
![]() $\gamma $
and g disagree. Hence for each g it is possible that
$\gamma $
and g disagree. Hence for each g it is possible that
![]() $\exists x (\overline {\gamma }(x)=\overline {g}(x) \wedge e(\overline {g}(x))>0$
. So for each g there is an x such that
$\exists x (\overline {\gamma }(x)=\overline {g}(x) \wedge e(\overline {g}(x))>0$
. So for each g there is an x such that
![]() $e(\overline {g}(x))>0$
.
$e(\overline {g}(x))>0$
.
Conversely, assume that
![]() $\forall g \exists x \, e(\overline {g}(x))>0$
. Let
$\forall g \exists x \, e(\overline {g}(x))>0$
. Let
![]() $C(n) :\leftrightarrow n\in Seq \wedge e(n)=0 $
. So C holds of the sequence numbers that a choice sequence
$C(n) :\leftrightarrow n\in Seq \wedge e(n)=0 $
. So C holds of the sequence numbers that a choice sequence
![]() $\alpha $
could go through and still have
$\alpha $
could go through and still have
![]() $e(\mathrm {is} \alpha )$
be 0. By the assumption, C is quasi-treelike and well-founded. (In fact, C will define a tree.) So by S5 it is inevitable that
$e(\mathrm {is} \alpha )$
be 0. By the assumption, C is quasi-treelike and well-founded. (In fact, C will define a tree.) So by S5 it is inevitable that
![]() $\alpha $
leaves C. That is, it is inevitable that there is some x such that
$\alpha $
leaves C. That is, it is inevitable that there is some x such that
![]() $e(\overline {\alpha }(x))>0$
.
$e(\overline {\alpha }(x))>0$
.
This lemma is interesting for two reasons. First, it is technically useful because it reduces the property
![]() $(e\in K_0)^{\mathsf {B}}$
to something arithmetical and hence stable. Second, it is interesting because it shows that the neighborhood functions that encode continuous operations from lawless sequences to natural numbers also encode continuous operations from lawlike sequences (represented as classical functions) to natural numbers. This is a version of what has been called the extension principle in intuitionistic mathematics.Footnote
16
The extension principle admits of very compelling informal plausibility arguments, but it is nevertheless a substantive claim. That this version of the principle is actually provable in
$(e\in K_0)^{\mathsf {B}}$
to something arithmetical and hence stable. Second, it is interesting because it shows that the neighborhood functions that encode continuous operations from lawless sequences to natural numbers also encode continuous operations from lawlike sequences (represented as classical functions) to natural numbers. This is a version of what has been called the extension principle in intuitionistic mathematics.Footnote
16
The extension principle admits of very compelling informal plausibility arguments, but it is nevertheless a substantive claim. That this version of the principle is actually provable in
![]() $MC_{LS}$
is of some interest.
$MC_{LS}$
is of some interest.
We can also observe that neighborhood functions so defined really do encompass k-adic neighborhood functions in the way informally sketched in the discussion of Section 4.
Lemma 8.17.
 $MC_{LS} \vdash (e \in K_0)^{\mathsf {B}} {\kern-1pt}\rightarrow{\kern-1pt} \forall \alpha _1 \dots \forall \alpha _k \mathcal {I}\exists x \exists n {\kern-1pt}\in{\kern-1pt} Seq ( lh(n)=x \wedge \forall y<x \, (n)_y=\langle \alpha _1(y),\dots ,\alpha _k(y) \rangle \wedge e(n)>0 )$
.
$MC_{LS} \vdash (e \in K_0)^{\mathsf {B}} {\kern-1pt}\rightarrow{\kern-1pt} \forall \alpha _1 \dots \forall \alpha _k \mathcal {I}\exists x \exists n {\kern-1pt}\in{\kern-1pt} Seq ( lh(n)=x \wedge \forall y<x \, (n)_y=\langle \alpha _1(y),\dots ,\alpha _k(y) \rangle \wedge e(n)>0 )$
.
Proof Consider the formula
![]() $C(n):\leftrightarrow e(n)=0 \wedge \forall x<lh(n) \exists y_1,\dots ,y_k x=\langle y_1,\dots ,y_k\rangle $
. The
$C(n):\leftrightarrow e(n)=0 \wedge \forall x<lh(n) \exists y_1,\dots ,y_k x=\langle y_1,\dots ,y_k\rangle $
. The
![]() $\preceq $
-downward closure
$\preceq $
-downward closure
![]() $\overline {C}(m):\leftrightarrow \exists n(C(n) \wedge m \preceq n$
is then quasi-treelike, and by Lemma 8.16,
$\overline {C}(m):\leftrightarrow \exists n(C(n) \wedge m \preceq n$
is then quasi-treelike, and by Lemma 8.16,
![]() $\overline {C}$
will be well-founded. So inevitably
$\overline {C}$
will be well-founded. So inevitably
![]() $\vec {\alpha }$
will leave
$\vec {\alpha }$
will leave
![]() $\overline {C}$
. That is, inevitably
$\overline {C}$
. That is, inevitably
![]() $\exists x \exists n \in Seq ( lh(n)=x \wedge \forall y<x \, (n)_y=\langle \alpha _1(y),\dots ,\alpha _k(y) \rangle \wedge e(n)>0)$
.
$\exists x \exists n \in Seq ( lh(n)=x \wedge \forall y<x \, (n)_y=\langle \alpha _1(y),\dots ,\alpha _k(y) \rangle \wedge e(n)>0)$
.
Theorem 8.18.
![]() $MC_{LS} \vdash LS4_0^{\mathsf {B}}$
.
$MC_{LS} \vdash LS4_0^{\mathsf {B}}$
.
Proof Applying some obvious simplifications whose validity we have already established,
![]() $LS4_0^{\mathsf {B}}$
is
$LS4_0^{\mathsf {B}}$
is
 $$ \begin{align*} &\square \forall \vec{\alpha} \square \left( \bigwedge_{i,j} \neg\square \forall x \alpha_i(x)\simeq \alpha_j(x) \rightarrow \mathcal{I} \exists f A^{\mathsf{B}}(\vec{\alpha},f) \right) \\& \quad \rightarrow \mathcal{I} \exists e\in K_0 \square \forall n \square \left(\vphantom{\left( \bigwedge_{i,j} \neg\square \forall x \alpha_i(x)\simeq\alpha_j(x) \rightarrow A^{\mathsf{B}}(\vec{\alpha},f) \right)} e(n)>0 \rightarrow \mathcal{I} \exists f \square \forall \vec{\alpha}\in n \right.\\& \qquad\qquad\qquad\qquad\quad\qquad \square \left.\left( \bigwedge_{i,j} \neg\square \forall x \alpha_i(x)\simeq\alpha_j(x) \rightarrow A^{\mathsf{B}}(\vec{\alpha},f) \right) \right). \end{align*} $$
$$ \begin{align*} &\square \forall \vec{\alpha} \square \left( \bigwedge_{i,j} \neg\square \forall x \alpha_i(x)\simeq \alpha_j(x) \rightarrow \mathcal{I} \exists f A^{\mathsf{B}}(\vec{\alpha},f) \right) \\& \quad \rightarrow \mathcal{I} \exists e\in K_0 \square \forall n \square \left(\vphantom{\left( \bigwedge_{i,j} \neg\square \forall x \alpha_i(x)\simeq\alpha_j(x) \rightarrow A^{\mathsf{B}}(\vec{\alpha},f) \right)} e(n)>0 \rightarrow \mathcal{I} \exists f \square \forall \vec{\alpha}\in n \right.\\& \qquad\qquad\qquad\qquad\quad\qquad \square \left.\left( \bigwedge_{i,j} \neg\square \forall x \alpha_i(x)\simeq\alpha_j(x) \rightarrow A^{\mathsf{B}}(\vec{\alpha},f) \right) \right). \end{align*} $$
Suppose the antecedent of this large conditional holds. Then by Theorem 8.14 we know that for any pairwise distinct
![]() $\alpha $
’s,
$\alpha $
’s,
![]() $\forall \vec {n} [ \bigwedge _i \mathrm {is} \alpha _i=n_i \rightarrow \forall \vec {g}\in \vec {n}\exists \vec {y} \exists f T(A^{\mathsf {B}},\overrightarrow{g(y)})]$
.
$\forall \vec {n} [ \bigwedge _i \mathrm {is} \alpha _i=n_i \rightarrow \forall \vec {g}\in \vec {n}\exists \vec {y} \exists f T(A^{\mathsf {B}},\overrightarrow{g(y)})]$
.
Define the function e as follows. If n codes a k-tuple of sequences
![]() $\vec {n}$
but
$\vec {n}$
but
![]() $\neg \exists f T(A^{\mathsf {B}},\vec {n})$
, then
$\neg \exists f T(A^{\mathsf {B}},\vec {n})$
, then
![]() $e(n)=0$
. If n codes a k-tuple of sequences
$e(n)=0$
. If n codes a k-tuple of sequences
![]() $\vec {n}$
and
$\vec {n}$
and
![]() $ \exists f T(A^{\mathsf {B}},\vec {n})$
, then
$ \exists f T(A^{\mathsf {B}},\vec {n})$
, then
![]() $e(n)= 1$
. And, just so e is a well-defined function, if n does not code a k-tuple of sequences, put
$e(n)= 1$
. And, just so e is a well-defined function, if n does not code a k-tuple of sequences, put
![]() $e(n)=2$
. To ensure that e is a neighborhood function, we need to show that
$e(n)=2$
. To ensure that e is a neighborhood function, we need to show that
![]() $\forall \vec {g} \exists x \, e(\overline {g}(x))>0$
. For this, given the suppositions in place, it will suffice to show that for all
$\forall \vec {g} \exists x \, e(\overline {g}(x))>0$
. For this, given the suppositions in place, it will suffice to show that for all
![]() $\vec {g}$
there is some x such that it is possible to have
$\vec {g}$
there is some x such that it is possible to have
![]() $\bigwedge \mathrm {is} \alpha _i=\overline {g_i}(x)$
. Using S4 and S9, we can argue that for any functions
$\bigwedge \mathrm {is} \alpha _i=\overline {g_i}(x)$
. Using S4 and S9, we can argue that for any functions
![]() $g_1,\dots ,g_k$
it is possible for there to exist distinct
$g_1,\dots ,g_k$
it is possible for there to exist distinct
![]() $\alpha _1,\dots ,\alpha _k$
with respective initial segments
$\alpha _1,\dots ,\alpha _k$
with respective initial segments
![]() $\overline {g_1}(0),\dots ,\overline {g_k}(0)$
. Thus
$\overline {g_1}(0),\dots ,\overline {g_k}(0)$
. Thus
![]() $\forall \vec {g}\exists \vec {y} \exists f T(A^{\mathsf {B}},\overrightarrow{g(y)})$
. This ensures that e is indeed a neighborhood function.
$\forall \vec {g}\exists \vec {y} \exists f T(A^{\mathsf {B}},\overrightarrow{g(y)})$
. This ensures that e is indeed a neighborhood function.
Now suppose
![]() $e(n)>0$
. If
$e(n)>0$
. If
![]() $e(n)=2$
, let f be arbitrary; since there will not be any
$e(n)=2$
, let f be arbitrary; since there will not be any
![]() $\vec {\alpha }\in n$
in that case, the whole antecedent of our big conditional
$\vec {\alpha }\in n$
in that case, the whole antecedent of our big conditional
![]() $LS4_0^{\mathsf {B}}$
will hold trivially. But if
$LS4_0^{\mathsf {B}}$
will hold trivially. But if
![]() $e(n)=1$
, then n must code a k-tuple of sequences
$e(n)=1$
, then n must code a k-tuple of sequences
![]() $\vec {n}$
and we know that
$\vec {n}$
and we know that
![]() $\exists f T(A^{\mathsf {B}},\vec {n})$
. Let f be any such witness. By Lemma 8.10, we also know that for any
$\exists f T(A^{\mathsf {B}},\vec {n})$
. Let f be any such witness. By Lemma 8.10, we also know that for any
![]() $\vec {m}\succeq \vec {n}$
,
$\vec {m}\succeq \vec {n}$
,
![]() $T(A^{\mathsf {B}},\vec {m})$
(where f occurs as a parameter). For any k distinct choice sequences
$T(A^{\mathsf {B}},\vec {m})$
(where f occurs as a parameter). For any k distinct choice sequences
![]() $\vec {\alpha }\in n$
, there will be some
$\vec {\alpha }\in n$
, there will be some
![]() $\vec {m}\succeq \vec {n}$
such that
$\vec {m}\succeq \vec {n}$
such that
![]() $\bigwedge _i \mathrm {is}\ \alpha _i=m_i$
; and hence by Theorem 8.14,
$\bigwedge _i \mathrm {is}\ \alpha _i=m_i$
; and hence by Theorem 8.14,
![]() $A^{\mathsf {B}}(\vec {\alpha },f)$
will hold.
$A^{\mathsf {B}}(\vec {\alpha },f)$
will hold.
As a slight digression, note that in this proof we had to appeal to an instance of the axiom of choice for a formula
![]() $\exists f T(A^{\mathsf {B}},\vec {n})$
—actually, a boolean combination of this formula with some
$\exists f T(A^{\mathsf {B}},\vec {n})$
—actually, a boolean combination of this formula with some
![]() $\Delta ^0_1$
formulas. The complexity of
$\Delta ^0_1$
formulas. The complexity of
![]() $T(A^{\mathsf {B}},\vec {n})$
can be bounded in terms of the complexity of A, but there are formulas
$T(A^{\mathsf {B}},\vec {n})$
can be bounded in terms of the complexity of A, but there are formulas
![]() $T(A^{\mathsf {B}},\vec {n})$
of arbitrarily high quantificational complexity. So, unlike the proofs of
$T(A^{\mathsf {B}},\vec {n})$
of arbitrarily high quantificational complexity. So, unlike the proofs of
![]() $LS1$
,
$LS1$
,
![]() $LS2$
, and
$LS2$
, and
![]() $LS3$
, this proof actually requires the strength of
$LS3$
, this proof actually requires the strength of
![]() $MC_{LS}$
with the full axiom of choice. It is open, however, whether a different proof might use weaker assumptions.
$MC_{LS}$
with the full axiom of choice. It is open, however, whether a different proof might use weaker assumptions.
Returning now to our discussion of
![]() $LS4$
, recall that the official version of
$LS4$
, recall that the official version of
![]() $LS4$
is formulated with the inductively defined class of functions K in place of the explicitly defined class
$LS4$
is formulated with the inductively defined class of functions K in place of the explicitly defined class
![]() $K_0$
. To directly define an analogous class K in
$K_0$
. To directly define an analogous class K in
![]() $MC_{LS}$
, I would have to extend
$MC_{LS}$
, I would have to extend
![]() $MC_{LS}$
to a stronger theory such as third-order arithmetic. Rather than do that, however, I will simply show that
$MC_{LS}$
to a stronger theory such as third-order arithmetic. Rather than do that, however, I will simply show that
![]() $K_0$
satisfies the inductive closure conditions and then show schematically that
$K_0$
satisfies the inductive closure conditions and then show schematically that
![]() $K_0$
is included in any other class that satisfies the inductive conditions. Then it will follow that any theory extending
$K_0$
is included in any other class that satisfies the inductive conditions. Then it will follow that any theory extending
![]() $MC_{LS}$
which is capable of formally defining K will interpret
$MC_{LS}$
which is capable of formally defining K will interpret
![]() $LS4$
. The limitation of
$LS4$
. The limitation of
![]() $MC_{LS}$
is merely in what definitions it can formalize, not in its deductive strength.
$MC_{LS}$
is merely in what definitions it can formalize, not in its deductive strength.
Make the following two abbreviations, which are schematic in the formula A:
-
•
 $\mathbf {K1}(A):\leftrightarrow \exists y>0 \forall x \, f(x)=y \rightarrow f\in A$
.
$\mathbf {K1}(A):\leftrightarrow \exists y>0 \forall x \, f(x)=y \rightarrow f\in A$
. -
•
 $\mathbf {K2}(A): \leftrightarrow [f(0)=0 \wedge \forall x \exists g\in A (\forall n\in Seq \, f(\langle x \rangle ^\frown n)=g(n))] \rightarrow f\in A$
.
$\mathbf {K2}(A): \leftrightarrow [f(0)=0 \wedge \forall x \exists g\in A (\forall n\in Seq \, f(\langle x \rangle ^\frown n)=g(n))] \rightarrow f\in A$
.
Then the following theorem is essentially the combination of Propositions 4.8.5 and 4.8.7 in [Reference Troelstra and van Dalen34].
Theorem 8.19.
![]() $MC_{LS}$
proves:
$MC_{LS}$
proves:
-
1.
 $\mathbf {K1}(K_0) \wedge \mathbf {K2}(K_0)$
.
$\mathbf {K1}(K_0) \wedge \mathbf {K2}(K_0)$
. -
2.
 $\mathbf {K1}(A) \wedge \mathbf {K2}(A) \rightarrow \forall f (f\in K_0 \rightarrow f\in A)$
.
$\mathbf {K1}(A) \wedge \mathbf {K2}(A) \rightarrow \forall f (f\in K_0 \rightarrow f\in A)$
.
Proof (1) That
![]() $\mathbf {K1}(K_0)$
is obvious. To see that
$\mathbf {K1}(K_0)$
is obvious. To see that
![]() $\mathbf {K2}(K_0)$
holds, suppose f satisfies the antecedent of
$\mathbf {K2}(K_0)$
holds, suppose f satisfies the antecedent of
![]() $\mathbf {K2}(K_0)$
, but
$\mathbf {K2}(K_0)$
, but
![]() $f\notin K_0$
. So
$f\notin K_0$
. So
![]() $\exists h \forall x f(\overline {h}(x))=0 \vee \exists n (f(n)> 0 \wedge \exists m\succeq n \, f(m)\neq f(n) )$
. The possibility that
$\exists h \forall x f(\overline {h}(x))=0 \vee \exists n (f(n)> 0 \wedge \exists m\succeq n \, f(m)\neq f(n) )$
. The possibility that
![]() $\exists n (f(n)> 0 \wedge \exists m\succeq n \, f(m)\neq f(n) )$
is ruled out by the fact that
$\exists n (f(n)> 0 \wedge \exists m\succeq n \, f(m)\neq f(n) )$
is ruled out by the fact that
![]() $f(0)=0 \wedge \forall x \exists g\in K_0 (\forall n\in Seq \, f(\langle x \rangle ^\frown n)=g(n))$
. So we must have that
$f(0)=0 \wedge \forall x \exists g\in K_0 (\forall n\in Seq \, f(\langle x \rangle ^\frown n)=g(n))$
. So we must have that
![]() $\exists h \forall x f(\overline {h}(x))=0$
. Let
$\exists h \forall x f(\overline {h}(x))=0$
. Let
![]() $h'(x):=h(x+1)$
. But then let
$h'(x):=h(x+1)$
. But then let
![]() $g\in K_0$
be the witness for
$g\in K_0$
be the witness for
![]() $f(\langle h(0) \rangle ^\frown n)=g(n)$
. So
$f(\langle h(0) \rangle ^\frown n)=g(n)$
. So
![]() $\forall x g(\overline {h'}(x))=0$
, which contradicts
$\forall x g(\overline {h'}(x))=0$
, which contradicts
![]() $g\in K_0$
.
$g\in K_0$
.
(2) Suppose
![]() $\mathbf {K1}(A) \wedge \mathbf {K2}(A)$
but that we have some
$\mathbf {K1}(A) \wedge \mathbf {K2}(A)$
but that we have some
![]() $f\in K_0$
but
$f\in K_0$
but
![]() $f\notin A$
. We can uniformly define the functions
$f\notin A$
. We can uniformly define the functions
![]() $g_n$
so that
$g_n$
so that
![]() $g_n(m)=f(n^\frown m)$
. Now since A satisfies
$g_n(m)=f(n^\frown m)$
. Now since A satisfies
![]() $\mathbf {K2}$
, we know that for every n, if
$\mathbf {K2}$
, we know that for every n, if
![]() $g_n \notin A$
, then there is an extension
$g_n \notin A$
, then there is an extension
![]() $n'\succ n$
with length
$n'\succ n$
with length
![]() $lh(n)+1$
such that
$lh(n)+1$
such that
![]() $g_{n'}\notin A$
. Thus by the axiom of dependent choice there is a function H enumerating these n such that
$g_{n'}\notin A$
. Thus by the axiom of dependent choice there is a function H enumerating these n such that
![]() $g_n\notin A$
. Then it is easy to define a function h such that
$g_n\notin A$
. Then it is easy to define a function h such that
![]() $\overline {h}(x)=H(x+1)$
. Since f is a neighborhood function, there will be some x such that for all
$\overline {h}(x)=H(x+1)$
. Since f is a neighborhood function, there will be some x such that for all
![]() $m\succeq \overline {h}(x)$
,
$m\succeq \overline {h}(x)$
,
![]() $f(m)=f(\overline {h}(x))>0$
. But then
$f(m)=f(\overline {h}(x))>0$
. But then
![]() $g_m$
is a constant, non-zero function, so
$g_m$
is a constant, non-zero function, so
![]() $g_m\in A$
, a contradiction.
$g_m\in A$
, a contradiction.
This theorem shows that
![]() $K_0$
is closed under the inductive clauses
$K_0$
is closed under the inductive clauses
![]() $\mathbf {K1}$
and
$\mathbf {K1}$
and
![]() $\mathbf {K2}$
and, schematically, for any other class which is also so closed,
$\mathbf {K2}$
and, schematically, for any other class which is also so closed,
![]() $K_0$
is included in that class. Since this latter fact is schematic, any extension of
$K_0$
is included in that class. Since this latter fact is schematic, any extension of
![]() $MC_{LS}$
that proved the existence of a least fixed point for the inductive clauses K1 and K2 would prove that
$MC_{LS}$
that proved the existence of a least fixed point for the inductive clauses K1 and K2 would prove that
![]() $K_0$
was that fixed point. Such an extension might for instance frame
$K_0$
was that fixed point. Such an extension might for instance frame
![]() $MC_{LS}$
in a background third-order arithmetic, or might extend the language with a new constant K for the fixed point, or might use some other means. More to the point, for present purposes, any proof in
$MC_{LS}$
in a background third-order arithmetic, or might extend the language with a new constant K for the fixed point, or might use some other means. More to the point, for present purposes, any proof in
![]() $LS$
that appeals to the minimality of K will appeal to a particular instance
$LS$
that appeals to the minimality of K will appeal to a particular instance
![]() $A\subseteq K$
; this can then be interpreted in
$A\subseteq K$
; this can then be interpreted in
![]() $MC_{LS}$
as
$MC_{LS}$
as
![]() $A \subseteq K_0$
, which we have just seen to be provable. All that matters is that the axiom of dependent choice can be applied to formulas of the form
$A \subseteq K_0$
, which we have just seen to be provable. All that matters is that the axiom of dependent choice can be applied to formulas of the form
![]() $g_n \notin A$
.
$g_n \notin A$
.
8.3 Elementary analysis and
 $IDB$
$IDB$
I have shown so far that
![]() $MC_{LS}$
proves the
$MC_{LS}$
proves the
![]() $\mathsf {B}$
translations of the axioms
$\mathsf {B}$
translations of the axioms
![]() $LS1$
–
$LS1$
–
![]() $LS4$
. The theory
$LS4$
. The theory
![]() $LS$
, however, is based on a background theory called
$LS$
, however, is based on a background theory called
![]() $IDB_1$
.Footnote
17
(
$IDB_1$
.Footnote
17
(
![]() $IDB$
stands for “inductively defined Brouwer-operations”.) Thus, the last thing to do to complete our interpretation of
$IDB$
stands for “inductively defined Brouwer-operations”.) Thus, the last thing to do to complete our interpretation of
![]() $LS$
is to show that
$LS$
is to show that
![]() $MC_{LS}$
proves the
$MC_{LS}$
proves the
![]() $\mathsf {B}$
translations of the axioms of
$\mathsf {B}$
translations of the axioms of
![]() $IDB_1$
.
$IDB_1$
.
![]() $IDB_1$
itself results from starting with the theory of elementary analysis known as
$IDB_1$
itself results from starting with the theory of elementary analysis known as
![]() $EL_1$
and adding to the language a constant K and axioms
$EL_1$
and adding to the language a constant K and axioms
![]() $\mathbf {K1}(K)$
,
$\mathbf {K1}(K)$
,
![]() $\mathbf {K2}(K)$
and the schema
$\mathbf {K2}(K)$
and the schema
![]() $\mathbf {K1}(A) \wedge \mathbf {K2}(A) \rightarrow K\subseteq A$
. This portion of the theory is handled by translating K as
$\mathbf {K1}(A) \wedge \mathbf {K2}(A) \rightarrow K\subseteq A$
. This portion of the theory is handled by translating K as
![]() $K_0$
and appealing to Theorem 8.19.
$K_0$
and appealing to Theorem 8.19.
The language of
![]() $EL_1$
consists of the language of arithmetic plus function symbols
$EL_1$
consists of the language of arithmetic plus function symbols
![]() $f,g,\dots $
, an abstraction operator
$f,g,\dots $
, an abstraction operator
![]() $\lambda $
, and a recursor
$\lambda $
, and a recursor
![]() $\mathsf {R}$
. The axioms are those of Heyting Arithmetic
$\mathsf {R}$
. The axioms are those of Heyting Arithmetic
![]() $HA$
, with induction extended to the full language of
$HA$
, with induction extended to the full language of
![]() $EL_1$
, the conversion axiom:
$EL_1$
, the conversion axiom:
and recursion axioms, where
![]() $\Phi $
is some unary functor:
$\Phi $
is some unary functor:
and finally, the axiom of choice for numbers and functions:
It is clear that we can omit
![]() $\lambda $
and
$\lambda $
and
![]() $\mathsf {R}$
from the development of
$\mathsf {R}$
from the development of
![]() $EL_1$
by appeal to the axiom of choice. Given any proof in
$EL_1$
by appeal to the axiom of choice. Given any proof in
![]() $EL_1$
that includes instances
$EL_1$
that includes instances
![]() $\lambda x.t(x)$
, we know
$\lambda x.t(x)$
, we know
![]() $\exists f \forall x f(x)=t(x)$
, and then replace each instance of
$\exists f \forall x f(x)=t(x)$
, and then replace each instance of
![]() $\lambda x.t(x)$
with
$\lambda x.t(x)$
with
![]() $f(x)$
throughout the proof. (In case there are instances of
$f(x)$
throughout the proof. (In case there are instances of
![]() $\lambda $
-abstracts that themselves contain
$\lambda $
-abstracts that themselves contain
![]() $\lambda $
-abstracts, we work from the inside out, gradually replacing more and more
$\lambda $
-abstracts, we work from the inside out, gradually replacing more and more
![]() $\lambda $
-abstracts.) Similarly, the axiom of choice allows us to prove the existence of a function g such that
$\lambda $
-abstracts.) Similarly, the axiom of choice allows us to prove the existence of a function g such that
![]() $\forall x g(x)=\mathsf {R}(t_1,\Phi ,x)$
, so we can replace instances of
$\forall x g(x)=\mathsf {R}(t_1,\Phi ,x)$
, so we can replace instances of
![]() $\mathsf {R}$
by function variables. Then since AC holds in
$\mathsf {R}$
by function variables. Then since AC holds in
![]() $MC_{LS}$
, we can interpret these modified proofs from which occurrences of
$MC_{LS}$
, we can interpret these modified proofs from which occurrences of
![]() $\lambda $
and
$\lambda $
and
![]() $\mathsf {R}$
have been removed.
$\mathsf {R}$
have been removed.
Next, we can observe that AC-NF holds in
![]() $MC_{LS}$
. Since
$MC_{LS}$
. Since
![]() $MC_{LS}$
includes second-order arithmetic, this is a standard result.
$MC_{LS}$
includes second-order arithmetic, this is a standard result.
Proposition 8.20.
![]() $MC_{LS}\vdash $
AC-NF.
$MC_{LS}\vdash $
AC-NF.
Proof Suppose
![]() $\forall x \exists f A(x,f)$
, and for simplicity suppose f is unary. Define a relation
$\forall x \exists f A(x,f)$
, and for simplicity suppose f is unary. Define a relation
![]() $f_1 \triangleleft f_2 :\leftrightarrow \exists x (f_1(x)< f_2(x) \wedge \forall y<x f_1(y)=f_2(y))$
. Then define
$f_1 \triangleleft f_2 :\leftrightarrow \exists x (f_1(x)< f_2(x) \wedge \forall y<x f_1(y)=f_2(y))$
. Then define
![]() $g(x,y)=z :\leftrightarrow \exists f [ A(x,f) \wedge f(y)=z \wedge \forall f' (A(x,f')\rightarrow f\triangleleft f' )]$
. To show that g is well-defined, we need to show that among the functions satisfying
$g(x,y)=z :\leftrightarrow \exists f [ A(x,f) \wedge f(y)=z \wedge \forall f' (A(x,f')\rightarrow f\triangleleft f' )]$
. To show that g is well-defined, we need to show that among the functions satisfying
![]() $A(x,f)$
there indeed one which is
$A(x,f)$
there indeed one which is
![]() $\triangleleft $
-least among them. Consider the set
$\triangleleft $
-least among them. Consider the set
 $X =\lbrace \langle y,z \rangle : \exists f_1 \exists f_2 [A(x,f_1) \wedge A(x,f_2) \wedge f_1(y)=z < f_2(y) \wedge \forall w<y f_1(w)=f_2(w) \rbrace $
. In other words,
$X =\lbrace \langle y,z \rangle : \exists f_1 \exists f_2 [A(x,f_1) \wedge A(x,f_2) \wedge f_1(y)=z < f_2(y) \wedge \forall w<y f_1(w)=f_2(w) \rbrace $
. In other words,
![]() $\langle y,z\rangle $
is the argument-value pair that witnesses
$\langle y,z\rangle $
is the argument-value pair that witnesses
![]() $f_1\triangleleft f_2$
. Now if there were no
$f_1\triangleleft f_2$
. Now if there were no
![]() $\triangleleft $
-least function satisfying A, then (using QF-DC) the lexicographic ordering of X would not be well-founded, which is impossible.
$\triangleleft $
-least function satisfying A, then (using QF-DC) the lexicographic ordering of X would not be well-founded, which is impossible.
Finally, the axioms of
![]() $HA$
—which are, of course, the same as the axioms of
$HA$
—which are, of course, the same as the axioms of
![]() $PA$
—will be equivalent to their
$PA$
—will be equivalent to their
![]() $\mathsf {B}$
translations by stability. Putting all this together, we have the main theorem:
$\mathsf {B}$
translations by stability. Putting all this together, we have the main theorem:
Theorem 8.21.
![]() $MC_{LS}$
interprets the theory
$MC_{LS}$
interprets the theory
![]() $LS$
under the translation
$LS$
under the translation
![]() $\mathsf {B}$
.
$\mathsf {B}$
.
Obviously, this interpretation is not faithful. That is, there are non-theorems of
![]() $LS$
whose
$LS$
whose
![]() $\mathsf {B}$
translations will be theorems of
$\mathsf {B}$
translations will be theorems of
![]() $MC_{LS}$
. Indeed, there will be non-theorems A of
$MC_{LS}$
. Indeed, there will be non-theorems A of
![]() $EL_1$
such that
$EL_1$
such that
![]() $MC_{LS}\vdash A^{\mathsf {B}}$
. This is a consequence of the fact that the arithmetic portion of
$MC_{LS}\vdash A^{\mathsf {B}}$
. This is a consequence of the fact that the arithmetic portion of
![]() $MC_{LS}$
is both classical and equivalent to its
$MC_{LS}$
is both classical and equivalent to its
![]() $\mathsf {B}$
-translation.
$\mathsf {B}$
-translation.
The fact that
![]() $EL_1^{\mathsf {B}}$
is equivalent in
$EL_1^{\mathsf {B}}$
is equivalent in
![]() $MC_{LS}$
to the result of erasing all modal operators is the reason we have had to include such strong choice principles and the full schema of induction. AC-NF being an axiom of
$MC_{LS}$
to the result of erasing all modal operators is the reason we have had to include such strong choice principles and the full schema of induction. AC-NF being an axiom of
![]() $EL_1$
requires that AC-NF
$EL_1$
requires that AC-NF
![]() $^{\mathsf {B}}$
, and hence AC-NF itself, be a theorem of
$^{\mathsf {B}}$
, and hence AC-NF itself, be a theorem of
![]() $MC_{LS}$
. Likewise, since
$MC_{LS}$
. Likewise, since
![]() $EL_1$
includes every instance of the schema of induction,
$EL_1$
includes every instance of the schema of induction,
![]() $MC_{LS}$
also needs to include every instance in order to interpret
$MC_{LS}$
also needs to include every instance in order to interpret
![]() $EL_1$
via
$EL_1$
via
![]() $\mathsf {B}$
.
$\mathsf {B}$
.
On the other hand, the interpretation of
![]() $LS1$
–
$LS1$
–
![]() $LS3$
required no essential use of induction and only
$LS3$
required no essential use of induction and only
![]() $\Delta ^0_1$
-AC. (In inferring that various formulas were quasi-treelike, I often implicitly assumed that function-existence was closed under recursive operations.) On the other hand, as I observed above, the interpretation of
$\Delta ^0_1$
-AC. (In inferring that various formulas were quasi-treelike, I often implicitly assumed that function-existence was closed under recursive operations.) On the other hand, as I observed above, the interpretation of
![]() $LS4$
seems to require the full axiom of choice. Given that
$LS4$
seems to require the full axiom of choice. Given that
![]() $LS4$
requires the existence of a sufficiently inclusive class of neighborhood functions, it is perhaps not surprising that this requires a commitment to strong function existence principles. With the exception of assuming that there are enough classical functions, however, the principles about choice sequences per se require very little mathematical strength. They are all provable on the basis of our philosophically well-motivated axioms S1–S9. And as we will see in the next section, these axioms have very little mathematical strength on their own.
$LS4$
requires the existence of a sufficiently inclusive class of neighborhood functions, it is perhaps not surprising that this requires a commitment to strong function existence principles. With the exception of assuming that there are enough classical functions, however, the principles about choice sequences per se require very little mathematical strength. They are all provable on the basis of our philosophically well-motivated axioms S1–S9. And as we will see in the next section, these axioms have very little mathematical strength on their own.
9
 $MC_{LS}$
and classical theories
$MC_{LS}$
and classical theories
In this section I study the relation between the modal three-sorted theory
![]() $MC_{LS}$
and the standard non-modal two-sorted theories of second-order arithmetic. Given a familiar theory Z of second-order arithmetic, let
$MC_{LS}$
and the standard non-modal two-sorted theories of second-order arithmetic. Given a familiar theory Z of second-order arithmetic, let
![]() $MC_{LS}(Z)$
be the theory like
$MC_{LS}(Z)$
be the theory like
![]() $MC_{LS}$
except that the arithmetical axioms are those of Z. For instance,
$MC_{LS}$
except that the arithmetical axioms are those of Z. For instance,
![]() $MC_{LS}(RCA_0)$
is the theory consisting of axioms A0–A9, and the induction schema restricted to
$MC_{LS}(RCA_0)$
is the theory consisting of axioms A0–A9, and the induction schema restricted to
![]() $\Sigma ^0_1$
formulas, AC restricted to
$\Sigma ^0_1$
formulas, AC restricted to
![]() $\Delta ^0_1$
formulas, arithmetic stability axioms, and the axioms S1–S9. Then the main result of this section will be that if Z is any subsystem of second-order arithmetic extending
$\Delta ^0_1$
formulas, arithmetic stability axioms, and the axioms S1–S9. Then the main result of this section will be that if Z is any subsystem of second-order arithmetic extending
![]() $RCA_0$
, then
$RCA_0$
, then
![]() $MC_{LS}(Z)$
is conservative over Z. (The choice of
$MC_{LS}(Z)$
is conservative over Z. (The choice of
![]() $RCA_0$
is so that the basic coding of finite sequences and so forth is possible, as this is necessary for the meaningfulness of several of the sequence axioms.)
$RCA_0$
is so that the basic coding of finite sequences and so forth is possible, as this is necessary for the meaningfulness of several of the sequence axioms.)
To prove this, I will show how, given a countable model M of Z, we can define a partial order
![]() $\mathbb {P}$
that can serve as a Kripke model for
$\mathbb {P}$
that can serve as a Kripke model for
![]() $MC_{LS}$
. The key to this result is providing a non-standard interpretation of
$MC_{LS}$
. The key to this result is providing a non-standard interpretation of
![]() $\mathcal {I}$
in
$\mathcal {I}$
in
![]() $\mathbb {P}$
.Footnote
18
To distinguish this non-standard interpretation of the modal vocabulary from the standard, intended interpretation given in Section 4, I will use the expression “forcing” and the symbol
$\mathbb {P}$
.Footnote
18
To distinguish this non-standard interpretation of the modal vocabulary from the standard, intended interpretation given in Section 4, I will use the expression “forcing” and the symbol
![]() $\Vdash $
to refer to the interpretation in
$\Vdash $
to refer to the interpretation in
![]() $\mathbb {P}$
.Footnote
19
Then I will show that (1) all arithmetic formulas that are true in M are forced at every
$\mathbb {P}$
.Footnote
19
Then I will show that (1) all arithmetic formulas that are true in M are forced at every
![]() $w\in \mathbb {P}$
, (2) all the axioms of
$w\in \mathbb {P}$
, (2) all the axioms of
![]() $MC_{LS}(Z)$
are also forced at every
$MC_{LS}(Z)$
are also forced at every
![]() $w\in \mathbb {P}$
, and (3) that forcing is closed under
$w\in \mathbb {P}$
, and (3) that forcing is closed under
![]() $\mathbf {S4}_{\mathcal {I}}$
deducibility. Conservativity follows from these three facts.
$\mathbf {S4}_{\mathcal {I}}$
deducibility. Conservativity follows from these three facts.
Let M be a countable model of some subsystem of second-order arithmetic Z extending
![]() $RCA_0$
.
$RCA_0$
.
![]() $|M|$
will denote the first-order domain of Z, and
$|M|$
will denote the first-order domain of Z, and
![]() $S_M$
its second-order domain, that is, the functions of M. Let
$S_M$
its second-order domain, that is, the functions of M. Let
![]() $\langle w_k'\rangle _{k\in \mathbb {N}}$
be an enumeration of the functions that map natural numbers to
$\langle w_k'\rangle _{k\in \mathbb {N}}$
be an enumeration of the functions that map natural numbers to
![]() $Seq^M$
and that are non-zero on a finite set. (Recall that 0 codes the empty sequence
$Seq^M$
and that are non-zero on a finite set. (Recall that 0 codes the empty sequence
![]() $\langle \rangle $
.) Further, let
$\langle \rangle $
.) Further, let
![]() $w_0'$
be the constant 0 function. Let
$w_0'$
be the constant 0 function. Let
![]() $\langle n_k\rangle _{k\in \mathbb {N}}$
be an enumeration of
$\langle n_k\rangle _{k\in \mathbb {N}}$
be an enumeration of
![]() $Seq^M$
. Since M is countable, both of these enumerations will exist, though not necessarily in M. Now define a new enumeration
$Seq^M$
. Since M is countable, both of these enumerations will exist, though not necessarily in M. Now define a new enumeration
![]() $\langle w_k\rangle _{k\in \mathbb {N}}$
of functions as follows:
$\langle w_k\rangle _{k\in \mathbb {N}}$
of functions as follows:
![]() $w_0=w_0'$
, and for
$w_0=w_0'$
, and for
![]() $k>0$
, if
$k>0$
, if
![]() $i_1,\dots ,i_k$
are the least arguments on which
$i_1,\dots ,i_k$
are the least arguments on which
![]() $w_k'$
is 0, put
$w_k'$
is 0, put
![]() $w_k(i_j)=n_j$
for
$w_k(i_j)=n_j$
for
![]() $1\leq j\leq k$
and otherwise let
$1\leq j\leq k$
and otherwise let
![]() $w_k(x)=w_k'(x)$
.
$w_k(x)=w_k'(x)$
.
Let
![]() $\mathbb {P}_M$
be the set of functions
$\mathbb {P}_M$
be the set of functions
![]() $w_k$
, and define the relation
$w_k$
, and define the relation
![]() $w \sqsubseteq u$
to mean that whenever
$w \sqsubseteq u$
to mean that whenever
![]() $w(i)=n>0$
we have
$w(i)=n>0$
we have
![]() $u(i)=m$
, for some
$u(i)=m$
, for some
![]() $m \succeq n$
. Clearly
$m \succeq n$
. Clearly
![]() $(\mathbb {P}_M,\sqsubseteq )$
is a partial order with least element the constant zero function
$(\mathbb {P}_M,\sqsubseteq )$
is a partial order with least element the constant zero function
![]() $w_0$
. In general I will omit the subscript and just write
$w_0$
. In general I will omit the subscript and just write
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Also, define a variable assignment to be a function from choice sequence variables to natural numbers. I will use
![]() $\sigma $
, possibly subscripted, to denote a variable assignment;
$\sigma $
, possibly subscripted, to denote a variable assignment;
![]() $\sigma [\alpha \mapsto i]$
will denote the variable assignment that agrees with
$\sigma [\alpha \mapsto i]$
will denote the variable assignment that agrees with
![]() $\sigma $
except possibly on
$\sigma $
except possibly on
![]() $\alpha $
, which
$\alpha $
, which
![]() $\sigma $
maps to i. Since the functions
$\sigma $
maps to i. Since the functions
![]() $w$
serve as the worlds in our Kripke model, the idea is that, when
$w$
serve as the worlds in our Kripke model, the idea is that, when
![]() $\sigma (\alpha )=i$
,
$\sigma (\alpha )=i$
,
![]() $w(i)$
is interpreted as the initial segment of
$w(i)$
is interpreted as the initial segment of
![]() $\alpha $
.
$\alpha $
.
Recall the definition of the
![]() $\alpha ,n$
replacement
$\alpha ,n$
replacement
![]() $\mathcal{R}(P,\alpha ,n)$
from Definition 8.11. In particular, note that if
$\mathcal{R}(P,\alpha ,n)$
from Definition 8.11. In particular, note that if
![]() $\vec {\alpha }$
are all the choice sequence variables occurring in P, then
$\vec {\alpha }$
are all the choice sequence variables occurring in P, then
![]() $\mathcal{R}(P,\vec {\alpha },\vec {n})$
is arithmetic, and if P has no instances of choice sequence variables, then
$\mathcal{R}(P,\vec {\alpha },\vec {n})$
is arithmetic, and if P has no instances of choice sequence variables, then
![]() $\mathcal{R}(P,\alpha ,n)$
is just P.
$\mathcal{R}(P,\alpha ,n)$
is just P.
For the interpretation of
![]() $\mathcal {I}$
, we will need to define two new notions: the function
$\mathcal {I}$
, we will need to define two new notions: the function
![]() $w[f_i(x_i)]_I$
, and an
$w[f_i(x_i)]_I$
, and an
![]() $[f_i]_I$
-chain. This can be pronounced “f-I-chain.”
$[f_i]_I$
-chain. This can be pronounced “f-I-chain.”
Definition 9.1 (
 ${w[f_i(x_i)]_I}$
;
${w[f_i(x_i)]_I}$
;
 ${[f_i]_I}$
-Chain).
${[f_i]_I}$
-Chain).
Suppose we are given a node
![]() $w\in \mathbb {P}$
and some functions
$w\in \mathbb {P}$
and some functions
![]() $f_i\in S_M$
such that
$f_i\in S_M$
such that
![]() $f_i\in w(i)$
and numbers
$f_i\in w(i)$
and numbers
![]() $x_i\in |M|$
(with i ranging over some finite index set I of true natural numbers). Define the function
$x_i\in |M|$
(with i ranging over some finite index set I of true natural numbers). Define the function
![]() $ w[f_i(x_i)]_I$
as follows:
$ w[f_i(x_i)]_I$
as follows:
-
• If
 $j\notin I$
, then
$j\notin I$
, then
 $w[f_i(x_i)]_I(j)=w(j)$
.
$w[f_i(x_i)]_I(j)=w(j)$
. -
• If
 $i\in I$
but
$i\in I$
but
 $x_i< lh(w(i))$
, then
$x_i< lh(w(i))$
, then
 $w[f_i(x_i)]_I(i)=w(i)$
.
$w[f_i(x_i)]_I(i)=w(i)$
. -
• If
 $i\in I$
and
$i\in I$
and
 $x_i\geq lh(w(i))$
, then
$x_i\geq lh(w(i))$
, then
 $w[f_i(x_i)]_I(i)=\overline {f_i}(x_i-1)$
.
$w[f_i(x_i)]_I(i)=\overline {f_i}(x_i-1)$
.
Note that this will be a well-defined function, but there is no guarantee that it will be a member of
![]() $\mathbb {P}$
. Now define an
$\mathbb {P}$
. Now define an
![]() $[f_i]_I$
-chain above w to be a maximal chain C above w such that:
$[f_i]_I$
-chain above w to be a maximal chain C above w such that:
-
• For every
 $u\in C$
there are some
$u\in C$
there are some
 $x_i$
such that u and
$x_i$
such that u and
 $w[f_i(x_i)]_I$
agree on arguments from I.
$w[f_i(x_i)]_I$
agree on arguments from I. -
• For every
 $x_i\in |M|$
there is some
$x_i\in |M|$
there is some
 $u\in C$
such that for all
$u\in C$
such that for all
 $i\in I$
,
$i\in I$
,
 $u(i)\succeq \overline {f_i}(x_i)$
.
$u(i)\succeq \overline {f_i}(x_i)$
.
It is not difficult to see that f-I-chains exist:
Lemma 9.2. For any
![]() $w\in \mathbb {P}$
, any non-empty finite set of natural numbers I, and any functions
$w\in \mathbb {P}$
, any non-empty finite set of natural numbers I, and any functions
![]() $f_i\in S_M$
(indexed by
$f_i\in S_M$
(indexed by
![]() $i\in I$
) such that
$i\in I$
) such that
![]() $f_i\in w(i)$
, there exists an
$f_i\in w(i)$
, there exists an
![]() $[f_i]_I$
-chain C above w.
$[f_i]_I$
-chain C above w.
Proof It is easy to see that for any
![]() $u\in \mathbb {P}$
that agrees with
$u\in \mathbb {P}$
that agrees with
![]() $w[f_i(x_i)]_I$
on I, and any
$w[f_i(x_i)]_I$
on I, and any
![]() $y_i> x_i$
, there is some
$y_i> x_i$
, there is some
![]() $v\in \mathbb {P}$
such that
$v\in \mathbb {P}$
such that
![]() $v\sqsupseteq u$
and
$v\sqsupseteq u$
and
![]() $w[f_i(y_i)]_I$
and v agree on I. Let
$w[f_i(y_i)]_I$
and v agree on I. Let
![]() $\langle x_j \rangle _{j\in \mathbb {N}}$
be cofinal in
$\langle x_j \rangle _{j\in \mathbb {N}}$
be cofinal in
![]() $|M|$
(under the
$|M|$
(under the
![]() $<^M$
relation), and let
$<^M$
relation), and let
![]() $v_i$
be an enumeration of worlds such that
$v_i$
be an enumeration of worlds such that
![]() $v_j$
and
$v_j$
and
![]() $w[f_i(x_j)]_I$
agree on I. For each j we can (using the axiom of choice) define a maximal set
$w[f_i(x_j)]_I$
agree on I. For each j we can (using the axiom of choice) define a maximal set
![]() $C_j\subseteq \lbrace u : v_j \sqsupseteq u \sqsupseteq v_{j+1} \rbrace $
that is linearly ordered by
$C_j\subseteq \lbrace u : v_j \sqsupseteq u \sqsupseteq v_{j+1} \rbrace $
that is linearly ordered by
![]() $\sqsupset $
. Then
$\sqsupset $
. Then
![]() $C=\bigcup _j C_j$
is an
$C=\bigcup _j C_j$
is an
![]() $[f_i]_I$
-chain. It is easy to see that it satisfies the two conditions:
$[f_i]_I$
-chain. It is easy to see that it satisfies the two conditions:
-
• For every
 $u\in C$
there are some
$u\in C$
there are some
 $x_i$
such that u and
$x_i$
such that u and
 $w[f_i(x_i)]_I$
agree on I.
$w[f_i(x_i)]_I$
agree on I. -
• For every
 $x_i\in |M|$
there is some
$x_i\in |M|$
there is some
 $u\in C$
such that for all
$u\in C$
such that for all
 $i\in I$
,
$i\in I$
,
 $u(i)\succeq \overline {f_i}(x_i)$
.
$u(i)\succeq \overline {f_i}(x_i)$
.
And the fact that C is a maximal chain above w follows from the fact that the enumeration
![]() $\langle x_j \rangle _{j\in \mathbb {N}}$
was cofinal in
$\langle x_j \rangle _{j\in \mathbb {N}}$
was cofinal in
![]() $|M|$
.
$|M|$
.
Now we can define the forcing relation that will provide an interpretation of
![]() $MC_{LS}(Z)$
. I will assume that the background metatheory has a name for every
$MC_{LS}(Z)$
. I will assume that the background metatheory has a name for every
![]() $x\in |M|$
and
$x\in |M|$
and
![]() $f\in S_M$
.
$f\in S_M$
.
Definition 9.3. Define the forcing relation
![]() $w,\sigma \Vdash A$
inductively as follows:
$w,\sigma \Vdash A$
inductively as follows:
-
•
 $w,\sigma \Vdash P$
iff
$w,\sigma \Vdash P$
iff
 $M \models \mathcal{R}(P,\vec {\alpha },w(\sigma (\alpha )))$
.Footnote
20
$M \models \mathcal{R}(P,\vec {\alpha },w(\sigma (\alpha )))$
.Footnote
20
-
•
 $w,\sigma \Vdash \neg A$
iff
$w,\sigma \Vdash \neg A$
iff
 $w,\sigma \nVdash A$
.
$w,\sigma \nVdash A$
. -
•
 $w, \sigma \Vdash A\wedge B$
iff
$w, \sigma \Vdash A\wedge B$
iff
 $w, \sigma \Vdash A$
and
$w, \sigma \Vdash A$
and
 $w, \sigma \Vdash B$
.
$w, \sigma \Vdash B$
. -
•
 $w, \sigma \Vdash A\vee B$
iff
$w, \sigma \Vdash A\vee B$
iff
 $w,\sigma \Vdash A$
or
$w,\sigma \Vdash A$
or
 $w, \sigma \Vdash B$
.
$w, \sigma \Vdash B$
. -
•
 $w, \sigma \Vdash A \rightarrow B$
iff
$w, \sigma \Vdash A \rightarrow B$
iff
 $w, \sigma \nVdash A$
or
$w, \sigma \nVdash A$
or
 $ w, \sigma \Vdash B$
.
$ w, \sigma \Vdash B$
. -
•
 $w, \sigma \Vdash \forall x A$
iff
$w, \sigma \Vdash \forall x A$
iff
 $ \forall x (w, \sigma \Vdash A)$
.
$ \forall x (w, \sigma \Vdash A)$
. -
•
 $w, \sigma \Vdash \exists x A$
iff
$w, \sigma \Vdash \exists x A$
iff
 $ \exists x (w, \sigma \Vdash A)$
.
$ \exists x (w, \sigma \Vdash A)$
. -
•
 $w, \sigma \Vdash \forall f A$
iff
$w, \sigma \Vdash \forall f A$
iff
 $ \forall f (w, \sigma \Vdash A)$
.
$ \forall f (w, \sigma \Vdash A)$
. -
•
 $w, \sigma \Vdash \exists f A$
iff
$w, \sigma \Vdash \exists f A$
iff
 $ \exists f (w, \sigma \Vdash A)$
.
$ \exists f (w, \sigma \Vdash A)$
. -
•
 $w, \sigma \Vdash \forall \alpha A$
iff
$w, \sigma \Vdash \forall \alpha A$
iff
 $ \forall i ( w, \sigma [\alpha \mapsto i] \Vdash A)$
.
$ \forall i ( w, \sigma [\alpha \mapsto i] \Vdash A)$
. -
•
 $w, \sigma \Vdash \exists \alpha A$
iff
$w, \sigma \Vdash \exists \alpha A$
iff
 $ \exists i ( w, \sigma [\alpha \mapsto i] \Vdash A)$
.
$ \exists i ( w, \sigma [\alpha \mapsto i] \Vdash A)$
. -
•
 $w, \sigma \Vdash \square A$
iff
$w, \sigma \Vdash \square A$
iff
 $\forall u \sqsupseteq w ( u,\sigma \Vdash A)$
.
$\forall u \sqsupseteq w ( u,\sigma \Vdash A)$
. -
•
 $w, \sigma \Vdash \lozenge A$
iff
$w, \sigma \Vdash \lozenge A$
iff
 $\exists u \sqsupseteq w ( u,\sigma \Vdash A)$
.
$\exists u \sqsupseteq w ( u,\sigma \Vdash A)$
. -
•
 $w, \sigma \Vdash \mathcal {I} A$
iff for every non-empty finite index set
$w, \sigma \Vdash \mathcal {I} A$
iff for every non-empty finite index set
 $I\supseteq \lbrace \sigma (\alpha ) : \alpha \mathrm {~is~free~in~} A\rbrace $
, every
$I\supseteq \lbrace \sigma (\alpha ) : \alpha \mathrm {~is~free~in~} A\rbrace $
, every
 $f_i\in w(i)$
, and every
$f_i\in w(i)$
, and every
 $[f_i]_I$
-chain C, there is some
$[f_i]_I$
-chain C, there is some
 $u\in C$
such that
$u\in C$
such that
 $u,\sigma \Vdash A$
.
$u,\sigma \Vdash A$
.
The intuitive idea behind the clause for
![]() $\mathcal {I}$
is that, fixing some
$\mathcal {I}$
is that, fixing some
![]() $f_i$
’s, the extensions
$f_i$
’s, the extensions
![]() $ w[f_i(x_i)]_I$
of
$ w[f_i(x_i)]_I$
of
![]() $w$
trace out a possible future history of how the choice sequences assigned to members of I evolve. Considering all index sets I that include at least the free variables of A is a way of saying that this happens for every possible future history, which is the intended meaning of
$w$
trace out a possible future history of how the choice sequences assigned to members of I evolve. Considering all index sets I that include at least the free variables of A is a way of saying that this happens for every possible future history, which is the intended meaning of
![]() $\mathcal {I}$
. The extra complications involving the chain C come from the fact that the function
$\mathcal {I}$
. The extra complications involving the chain C come from the fact that the function
![]() $ w[f_i(x_i)]_I$
may not be in
$ w[f_i(x_i)]_I$
may not be in
![]() $\mathbb {P}$
. An
$\mathbb {P}$
. An
![]() $[f_i]_I$
-chain is a way of approximating the path of extensions
$[f_i]_I$
-chain is a way of approximating the path of extensions
![]() $ w[f_i(x_i)]_I$
within
$ w[f_i(x_i)]_I$
within
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Note that a formula
![]() $w,\sigma \Vdash A$
may have free variables; in fact, the free variables of this formula will be w,
$w,\sigma \Vdash A$
may have free variables; in fact, the free variables of this formula will be w,
![]() $\sigma $
, and the free number and classical function variables of A.
$\sigma $
, and the free number and classical function variables of A.
As usual, we can say that
![]() $w\Vdash A$
when
$w\Vdash A$
when
![]() $w,\sigma \Vdash A$
for all
$w,\sigma \Vdash A$
for all
![]() $\sigma $
. And it is easy to see that if A is a sentence, then
$\sigma $
. And it is easy to see that if A is a sentence, then
![]() $w, \sigma \Vdash A$
for some
$w, \sigma \Vdash A$
for some
![]() $\sigma $
iff
$\sigma $
iff
![]() $w, \sigma \Vdash A$
for all
$w, \sigma \Vdash A$
for all
![]() $\sigma $
.
$\sigma $
.
As an exercise in applying definitions, one can verify the following simple facts:
Proposition 9.4.
-
1.
 $w,\sigma \Vdash \alpha \in n$
iff
$w,\sigma \Vdash \alpha \in n$
iff
 $w(\sigma (\alpha ))\succeq n$
.
$w(\sigma (\alpha ))\succeq n$
. -
2. If
 $w,\sigma \Vdash \alpha \in n$
then
$w,\sigma \Vdash \alpha \in n$
then
 $w,\sigma \Vdash \square \alpha \in n$
.
$w,\sigma \Vdash \square \alpha \in n$
. -
3.
 $w,\sigma \Vdash \mathrm {is} \alpha =n$
iff
$w,\sigma \Vdash \mathrm {is} \alpha =n$
iff
 $w(\sigma (\alpha ))=n$
$w(\sigma (\alpha ))=n$
-
4.
 $w,\sigma \Vdash \square \forall x \alpha \simeq \beta $
iff
$w,\sigma \Vdash \square \forall x \alpha \simeq \beta $
iff
 $w(\sigma (\alpha ))=w(\sigma (\beta ))$
.
$w(\sigma (\alpha ))=w(\sigma (\beta ))$
.
It is also easy to see that the forcing definition coincides with truth in M for arithmetical formulas:
Theorem 9.5. If A is a formula of the language of Z and M is any Z-model, then for any
![]() $w,\ w \Vdash A$
iff
$w,\ w \Vdash A$
iff
![]() $M\models A$
.
$M\models A$
.
Proof Induction on the complexity of A. Straightforward.
Next, we want to observe that the axioms of
![]() $MC_{LS}$
are forced.
$MC_{LS}$
are forced.
Theorem 9.6. Every axiom of
![]() $MC_{LS}(Z)$
is forced at every
$MC_{LS}(Z)$
is forced at every
![]() $w\in \mathbb {P}$
.
$w\in \mathbb {P}$
.
This proof just consists in checking each axiom. The details are in Appendix C. Then, by checking that each axiom of
![]() $\mathbf {S4}_{\mathcal {I}}$
is forced everywhere, and that the inference rules of
$\mathbf {S4}_{\mathcal {I}}$
is forced everywhere, and that the inference rules of
![]() $\mathbf {S4}_{\mathcal {I}}$
preserve the property of being forced everywhere, we can establish:
$\mathbf {S4}_{\mathcal {I}}$
preserve the property of being forced everywhere, we can establish:
Theorem 9.7. Every theorem of
![]() $MC_{LS}(Z)$
is forced at every
$MC_{LS}(Z)$
is forced at every
![]() $w\in \mathbb {P}$
.
$w\in \mathbb {P}$
.
The proof, again, is in Appendix C. In summary, the theorems of this section entail our conservativity result.
Corollary 9.8. If Z is any subsystem of second-order arithmetic extending
![]() $RCA_0$
, and A is any formula in the language of second-order arithmetic, then
$RCA_0$
, and A is any formula in the language of second-order arithmetic, then
![]() $MC_{LS}(Z)\vdash A$
only if
$MC_{LS}(Z)\vdash A$
only if
![]() $Z\vdash A$
.
$Z\vdash A$
.
A Axioms for free many-sorted S4
I present a formulation of S4 to which the axioms M1–M7 can be added to obtain
![]() $\mathbf {S4}_{\mathcal {I}}$
. This axiomatization is based on a standard list such as can be found in [Reference Hughes and Cresswell19, 292ff], but with some tweaks in the quantifier rules. We have three sorts of variables, namely
$\mathbf {S4}_{\mathcal {I}}$
. This axiomatization is based on a standard list such as can be found in [Reference Hughes and Cresswell19, 292ff], but with some tweaks in the quantifier rules. We have three sorts of variables, namely
![]() $x,y,z$
for individuals,
$x,y,z$
for individuals,
![]() $f,g,h$
for classical functions, and
$f,g,h$
for classical functions, and
![]() $\alpha ,\beta ,\gamma $
for choice sequences, with the latter two of course being distinct sorts of functions on individuals.
$\alpha ,\beta ,\gamma $
for choice sequences, with the latter two of course being distinct sorts of functions on individuals.
-
M0.0 Any instance of a propositional S4 theorem schema.
-
M0.1
 $(\forall x Ax \wedge t=t)\rightarrow At$
, when x is an individual variable and t is any individual term.
$(\forall x Ax \wedge t=t)\rightarrow At$
, when x is an individual variable and t is any individual term. -
M0.2
 $\forall f Af \rightarrow Ag$
, letting g be any classical function term (since there are more than just variables).
$\forall f Af \rightarrow Ag$
, letting g be any classical function term (since there are more than just variables). -
M0.3
 $\forall \beta A\beta \rightarrow A\alpha $
.
$\forall \beta A\beta \rightarrow A\alpha $
. -
M0.4
 $\forall o(A \rightarrow B) \rightarrow (\forall o A \rightarrow \forall o B)$
, where o is a variable of any type.
$\forall o(A \rightarrow B) \rightarrow (\forall o A \rightarrow \forall o B)$
, where o is a variable of any type. -
M0.5
 $A \leftrightarrow \forall o A$
, when o is not free in A, for o a variable of any type.
$A \leftrightarrow \forall o A$
, when o is not free in A, for o a variable of any type. -
M0.6
 $\forall x (x=x)$
.
$\forall x (x=x)$
. -
M0.7
 $(t_1=t_1 \wedge t_2=t_2 \wedge t_1\neq t_2) \rightarrow \square t_1\neq t_2$
.
$(t_1=t_1 \wedge t_2=t_2 \wedge t_1\neq t_2) \rightarrow \square t_1\neq t_2$
. -
M0.8
 $t_1=t_2 \rightarrow (At_1 \rightarrow At_2)$
.
$t_1=t_2 \rightarrow (At_1 \rightarrow At_2)$
. -
M0.9
 $Pt\rightarrow t=t$
, for P any atom and t any individual term.
$Pt\rightarrow t=t$
, for P any atom and t any individual term. -
M0.10
 $\square \forall o A \rightarrow \forall o \square A$
, for o a variable of any type.
$\square \forall o A \rightarrow \forall o \square A$
, for o a variable of any type. -
M0.11 From
 $\vdash A\rightarrow B$
and
$\vdash A\rightarrow B$
and
 $\vdash A$
, infer
$\vdash A$
, infer
 $\vdash B$
.
$\vdash B$
. -
M0.12 From
 $\vdash A$
infer
$\vdash A$
infer
 $\vdash \square A$
.
$\vdash \square A$
. -
M0.13 From
 $\vdash A$
infer
$\vdash A$
infer
 $\vdash \forall o A$
, for o a variable of any type.
$\vdash \forall o A$
, for o a variable of any type.
Since this is a negative free logic, the schema
![]() $t=t$
is being used as an existence predicate for t. Completeness of this axiomatization can be proved using the standard canonical model technique.
$t=t$
is being used as an existence predicate for t. Completeness of this axiomatization can be proved using the standard canonical model technique.
Given that this logic is meant to underlie
![]() $MC_{LS}$
, it is appropriate to assume that there are individual constants and constant terms for functions of the same type as f, but that there are only function variables, not terms, of type
$MC_{LS}$
, it is appropriate to assume that there are individual constants and constant terms for functions of the same type as f, but that there are only function variables, not terms, of type
![]() $\alpha $
.
$\alpha $
.
B Proof of the elimination theorem
Lemma B.1. Let
![]() $P(\vec {\alpha },\vec {x},\vec {f})$
be an atom with free variables shown. Then in
$P(\vec {\alpha },\vec {x},\vec {f})$
be an atom with free variables shown. Then in
![]() $MC_{LS}$
, we have that necessarily for all
$MC_{LS}$
, we have that necessarily for all
![]() $\vec {x}$
, and
$\vec {x}$
, and
![]() $\vec {f}$
:
$\vec {f}$
:
-
1.
 $\forall \alpha _1 \dots \forall \alpha _k \exists n_1 \dots \exists n_k \left ( \vec {\alpha }\in \vec {n} \wedge \left ( P(\alpha _1,\dots ,\alpha _k,\vec {x},\vec {f}) \rightarrow \forall g_1 \in n_1 \dots \forall g_k \in n_k P(g_1,\dots ,g_k,\vec {x},\vec {f}) \right ) \right )$
.
$\forall \alpha _1 \dots \forall \alpha _k \exists n_1 \dots \exists n_k \left ( \vec {\alpha }\in \vec {n} \wedge \left ( P(\alpha _1,\dots ,\alpha _k,\vec {x},\vec {f}) \rightarrow \forall g_1 \in n_1 \dots \forall g_k \in n_k P(g_1,\dots ,g_k,\vec {x},\vec {f}) \right ) \right )$
. -
2.
 $P(\vec {\alpha },\vec {x},\vec {f}) \rightarrow \exists \vec {n} (\vec {f}\in \vec {n} \wedge \mathcal {R}(P,\vec {f},\vec {n}))$
.
$P(\vec {\alpha },\vec {x},\vec {f}) \rightarrow \exists \vec {n} (\vec {f}\in \vec {n} \wedge \mathcal {R}(P,\vec {f},\vec {n}))$
. -
3.
 $ \forall n_1 \dots \forall n_k \left ( \forall g_1 \in n_1 \dots \forall g_k \in n_k P(g_1,\dots ,g_k,\vec {x},\vec {f}) \rightarrow \forall \alpha _1 \in n_1 \dots \forall \alpha _k \in n_k \mathcal {I} P(\alpha _1,\dots ,\alpha _k,\vec {x},\vec {f}) \right ) $
.
$ \forall n_1 \dots \forall n_k \left ( \forall g_1 \in n_1 \dots \forall g_k \in n_k P(g_1,\dots ,g_k,\vec {x},\vec {f}) \rightarrow \forall \alpha _1 \in n_1 \dots \forall \alpha _k \in n_k \mathcal {I} P(\alpha _1,\dots ,\alpha _k,\vec {x},\vec {f}) \right ) $
.
Proof (1) In light of Proposition 8.13, it suffices to show, reasoning within
![]() $MC_{LS}$
, that
$MC_{LS}$
, that
![]() $\mathcal {R}(P,\vec {\alpha },\vec {n}) \rightarrow \forall \vec {g}\in \vec {n} P(\vec {g})$
. Suppose that
$\mathcal {R}(P,\vec {\alpha },\vec {n}) \rightarrow \forall \vec {g}\in \vec {n} P(\vec {g})$
. Suppose that
![]() $\mathcal {R}(P,\vec {\alpha },\vec {n})$
holds. Then for
$\mathcal {R}(P,\vec {\alpha },\vec {n})$
holds. Then for
![]() $P'$
as in Definition 8.11, we know
$P'$
as in Definition 8.11, we know
![]() $P'$
holds, and for every occurrence of
$P'$
holds, and for every occurrence of
![]() $(n_{i_j})_{t^{\prime }_j}$
in
$(n_{i_j})_{t^{\prime }_j}$
in
![]() $P'$
,
$P'$
,
![]() $t^{\prime }_j <lh(n_{i_j})$
. So for any terms
$t^{\prime }_j <lh(n_{i_j})$
. So for any terms
![]() $s_j$
, if
$s_j$
, if
![]() $s_j=(n_{i_j})_{t^{\prime }_j}$
, the substitution
$s_j=(n_{i_j})_{t^{\prime }_j}$
, the substitution
![]() $P'[(n_{i_1})_{t_1}/s_1,\dots ,(n_{i_k})_{t_k}/s_k]$
will also hold. For any
$P'[(n_{i_1})_{t_1}/s_1,\dots ,(n_{i_k})_{t_k}/s_k]$
will also hold. For any
![]() $\vec {g}\in \vec {n}$
, we will have
$\vec {g}\in \vec {n}$
, we will have
![]() $g_{i_j}(t^{\prime }_j)=(n_{i_j})_{t^{\prime }_j})$
, and hence
$g_{i_j}(t^{\prime }_j)=(n_{i_j})_{t^{\prime }_j})$
, and hence
![]() $P'[(n_{i_1})_{t^{\prime }_1}/g_{i_1}(t^{\prime }_1),\dots ,(n_{i_k})_{t^{\prime }_k}/g_{i_k}(t^{\prime }_k)]$
. That is,
$P'[(n_{i_1})_{t^{\prime }_1}/g_{i_1}(t^{\prime }_1),\dots ,(n_{i_k})_{t^{\prime }_k}/g_{i_k}(t^{\prime }_k)]$
. That is,
![]() $P(\vec {g})$
, as required.
$P(\vec {g})$
, as required.
(2) Assume for simplicity that there is only one function variable f; the argument easily generalizes to any finite number of functions
![]() $\vec {f}$
. Suppose
$\vec {f}$
. Suppose
![]() $P(f)$
holds, and suppose
$P(f)$
holds, and suppose
![]() $f(t_1),\dots ,f(t_k)$
are all the occurrences of f in P. Provably there is some z which is the greater than each of
$f(t_1),\dots ,f(t_k)$
are all the occurrences of f in P. Provably there is some z which is the greater than each of
![]() $t_1,\dots ,t_k$
. Let
$t_1,\dots ,t_k$
. Let
![]() $n=\overline {f}(z)$
, so for all
$n=\overline {f}(z)$
, so for all
![]() $x\leq s$
,
$x\leq s$
,
![]() $(n)_x=f(x)$
. In particular,
$(n)_x=f(x)$
. In particular,
![]() $(n)_{t_i}=f(i)$
for each
$(n)_{t_i}=f(i)$
for each
![]() $i\leq k$
. Thus the result
$i\leq k$
. Thus the result
![]() $P'$
of successively substituting
$P'$
of successively substituting
![]() $(n)_{t_j}$
for each occurrence
$(n)_{t_j}$
for each occurrence
![]() $f(t_j)$
in P will also hold. That is,
$f(t_j)$
in P will also hold. That is,
![]() $\mathcal {R}(P,f,n)$
will hold.
$\mathcal {R}(P,f,n)$
will hold.
(3) Let
![]() $\vec {n}$
be arbitrary, and suppose
$\vec {n}$
be arbitrary, and suppose
![]() $\forall \vec {g}\in \vec {n}P\vec {g}$
. Consider the formula
$\forall \vec {g}\in \vec {n}P\vec {g}$
. Consider the formula
![]() $C(\vec {m}):\leftrightarrow \neg \mathcal {R}(P,\alpha _1,\dots ,\alpha _k,n_1^\frown m_1,\dots ,n_k^\frown m_k)$
. Clearly C is quasi-treelike and by the supposition and claim (2), C is well founded. So by S5 the
$C(\vec {m}):\leftrightarrow \neg \mathcal {R}(P,\alpha _1,\dots ,\alpha _k,n_1^\frown m_1,\dots ,n_k^\frown m_k)$
. Clearly C is quasi-treelike and by the supposition and claim (2), C is well founded. So by S5 the
![]() $\vec {\alpha }$
’s will inevitably leave C. That is, inevitably
$\vec {\alpha }$
’s will inevitably leave C. That is, inevitably
![]() $\bigwedge _i \mathrm {is} \alpha _i=n_i^\frown m_i \wedge \mathcal {R}(P,\alpha _1,\dots ,\alpha _k,n_1^\frown m_1,\dots ,n_k^\frown m_k)$
, and hence inevitably
$\bigwedge _i \mathrm {is} \alpha _i=n_i^\frown m_i \wedge \mathcal {R}(P,\alpha _1,\dots ,\alpha _k,n_1^\frown m_1,\dots ,n_k^\frown m_k)$
, and hence inevitably
![]() $P(\vec {\alpha })$
.
$P(\vec {\alpha })$
.
(Although it is not important for what follows, we can note that the arguments for (1) and (2) still go through when there are other choice sequence parameters
![]() $\vec {\beta }$
in P.)
$\vec {\beta }$
in P.)
Note that atoms are positively stable, so this lemma also holds with
![]() $\square P$
in place of P. Now we are able to prove the elimination theorem.
$\square P$
in place of P. Now we are able to prove the elimination theorem.
Proof of Theorem 8.14
We proceed by a (lengthy) induction on the complexity of A. For the sake of brevity, we may take it as a background assumption for the duration of this proof that distinct choice sequence variables
![]() $\alpha _i,\alpha _j$
denote distinct choice sequences and are not necessarily coextensive.
$\alpha _i,\alpha _j$
denote distinct choice sequences and are not necessarily coextensive.
Basis step: A will be of the form
![]() $\mathcal {I}\square P$
, for some atom P.
$\mathcal {I}\square P$
, for some atom P.
(
![]() $\Rightarrow $
) Suppose
$\Rightarrow $
) Suppose
![]() $\mathrm {is}\ \alpha _i=n_i$
but that
$\mathrm {is}\ \alpha _i=n_i$
but that
![]() $\exists \vec {g}\in \vec {n} \forall \vec {y} \exists \vec {h} \in \overline {g}(y) \neg P\vec {h}$
. Then by Lemma B.1(1), as long as each
$\exists \vec {g}\in \vec {n} \forall \vec {y} \exists \vec {h} \in \overline {g}(y) \neg P\vec {h}$
. Then by Lemma B.1(1), as long as each
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $g_i$
agree—that is, as long as each
$g_i$
agree—that is, as long as each
![]() $\mathrm {is}\ \alpha _i=\overline {g_i}(y)$
for some y—we will have that
$\mathrm {is}\ \alpha _i=\overline {g_i}(y)$
for some y—we will have that
![]() $\neg P\vec {\alpha }$
and hence
$\neg P\vec {\alpha }$
and hence
![]() $\neg \square P\vec {\alpha }$
. In other words, if
$\neg \square P\vec {\alpha }$
. In other words, if
![]() $\square P\vec {\alpha }$
, then some
$\square P\vec {\alpha }$
, then some
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $g_i$
disagree. So by M1, if it is inevitable that
$g_i$
disagree. So by M1, if it is inevitable that
![]() $\square P\vec {\alpha }$
, then it is inevitable that some
$\square P\vec {\alpha }$
, then it is inevitable that some
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $g_i$
disagree. Since by S8 it is not inevitable that any
$g_i$
disagree. Since by S8 it is not inevitable that any
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $g_i$
disagree, it follows that
$g_i$
disagree, it follows that
![]() $\neg \mathcal {I} \square P\vec {\alpha }$
. (This pattern of reasoning will be used often.)
$\neg \mathcal {I} \square P\vec {\alpha }$
. (This pattern of reasoning will be used often.)
(
![]() $\Leftarrow $
) Assume that
$\Leftarrow $
) Assume that
![]() $\mathrm {is} \alpha _i=n_i$
that
$\mathrm {is} \alpha _i=n_i$
that
![]() $\forall \vec {g}\in \vec {n}\exists \vec {y} \forall \vec {h}\in \overline {g}(y) P\vec {h}$
. Consider the formula
$\forall \vec {g}\in \vec {n}\exists \vec {y} \forall \vec {h}\in \overline {g}(y) P\vec {h}$
. Consider the formula
![]() $C(\vec {m}): \leftrightarrow \vec {n}\preceq \vec {m}\wedge \exists \vec {h} \in \vec {m} \neg P\vec {h}$
. C will be quasi-treelike,Footnote
21
and by our assumption it is well-founded. Hence it is inevitable that
$C(\vec {m}): \leftrightarrow \vec {n}\preceq \vec {m}\wedge \exists \vec {h} \in \vec {m} \neg P\vec {h}$
. C will be quasi-treelike,Footnote
21
and by our assumption it is well-founded. Hence it is inevitable that
![]() $\vec {\alpha }$
leaves C. That is, it is inevitable that
$\vec {\alpha }$
leaves C. That is, it is inevitable that
![]() $\bigwedge _i \mathrm {is} \alpha _i=s_i \wedge \forall \vec {h}\in \vec {s} P\vec {h}$
. Then with Lemma B.1(3), this entails
$\bigwedge _i \mathrm {is} \alpha _i=s_i \wedge \forall \vec {h}\in \vec {s} P\vec {h}$
. Then with Lemma B.1(3), this entails
![]() $\mathcal {I}\mathcal {I} P\vec {\alpha }$
and hence, because atoms are positively stable,
$\mathcal {I}\mathcal {I} P\vec {\alpha }$
and hence, because atoms are positively stable,
![]() $\mathcal {I}\square P\vec {\alpha }$
.
$\mathcal {I}\square P\vec {\alpha }$
.
We turn now to the induction step, broken into the obvious series of cases.
Case 1: A is
![]() $B\wedge C$
. This case follows directly from i.h.
$B\wedge C$
. This case follows directly from i.h.
Case 2: A is
![]() $\mathcal {I}(B\vee C)$
.
$\mathcal {I}(B\vee C)$
.
(
![]() $\Rightarrow $
) Suppose
$\Rightarrow $
) Suppose
![]() $\mathcal {I}(B\vee C)$
, and let
$\mathcal {I}(B\vee C)$
, and let
![]() $\mathrm {is} \alpha _i=n_i$
. Let
$\mathrm {is} \alpha _i=n_i$
. Let
![]() $\vec {g}\in \vec {n}$
be arbitrary. Then it is not inevitable that any
$\vec {g}\in \vec {n}$
be arbitrary. Then it is not inevitable that any
![]() $g_i$
and
$g_i$
and
![]() $\alpha _i$
disagree. Since it is inevitable that
$\alpha _i$
disagree. Since it is inevitable that
![]() $B\vee C$
, it must be possible that
$B\vee C$
, it must be possible that
![]() $\vec {g}$
and
$\vec {g}$
and
![]() $\vec {\alpha }$
agree and that
$\vec {\alpha }$
agree and that
![]() $B\alpha \vee C\alpha $
. That is,
$B\alpha \vee C\alpha $
. That is,
![]() $\lozenge \exists \vec {y}( \bigwedge _i \mathrm {is} \alpha _i=\overline {g_i}(y_i) \wedge (B\alpha \vee C\alpha ))$
. Then by i.h.
$\lozenge \exists \vec {y}( \bigwedge _i \mathrm {is} \alpha _i=\overline {g_i}(y_i) \wedge (B\alpha \vee C\alpha ))$
. Then by i.h.
![]() $T(B,\overline {g_1}(y_1),\dots ,\overline {g_k}(y_k)) \vee T(C,\overline {g_1}(y_1),\dots ,\overline {g_k}(y_k))$
. Since
$T(B,\overline {g_1}(y_1),\dots ,\overline {g_k}(y_k)) \vee T(C,\overline {g_1}(y_1),\dots ,\overline {g_k}(y_k))$
. Since
![]() $\vec {g}\in \vec {n}$
was arbitrary, this gives the desired result.
$\vec {g}\in \vec {n}$
was arbitrary, this gives the desired result.
(
![]() $\Leftarrow $
) Suppose
$\Leftarrow $
) Suppose
![]() $\mathrm {is} \alpha _i=n_i$
and
$\mathrm {is} \alpha _i=n_i$
and
![]() $\forall \vec {g}\in \vec {n} \exists \vec {y}(T(B,\overline {g_1}(y_1),\dots ,\overline {g_k}(y_k)) \vee T(C,\overline {g_1}(y_1),\dots ,\overline {g_k}(y_k))$
. Let
$\forall \vec {g}\in \vec {n} \exists \vec {y}(T(B,\overline {g_1}(y_1),\dots ,\overline {g_k}(y_k)) \vee T(C,\overline {g_1}(y_1),\dots ,\overline {g_k}(y_k))$
. Let
![]() $C(\vec {m})$
be the formula
$C(\vec {m})$
be the formula
![]() $ \bigwedge _i n_i \preceq m_i \wedge \neg T(B,\vec {m}) \wedge \neg T(C,\vec {m}) $
. C will be quasi-treelike and well-founded, so it is inevitable that
$ \bigwedge _i n_i \preceq m_i \wedge \neg T(B,\vec {m}) \wedge \neg T(C,\vec {m}) $
. C will be quasi-treelike and well-founded, so it is inevitable that
![]() $\vec {\alpha }$
leaves C. So it is also inevitable that
$\vec {\alpha }$
leaves C. So it is also inevitable that
 $$ \begin{align*}\exists\vec{m} \left( \bigwedge_i \mathrm{is} \alpha_i=m_i \wedge (T(B,\vec{m}) \vee T(C,\vec{m}) ) \right).\end{align*} $$
$$ \begin{align*}\exists\vec{m} \left( \bigwedge_i \mathrm{is} \alpha_i=m_i \wedge (T(B,\vec{m}) \vee T(C,\vec{m}) ) \right).\end{align*} $$
Hence by i.h.
![]() $\mathcal {I}(B\vec {\alpha } \vee C\vec {\alpha })$
.
$\mathcal {I}(B\vec {\alpha } \vee C\vec {\alpha })$
.
Case 3: A is
![]() $\square \neg B$
.
$\square \neg B$
.
(
![]() $\Rightarrow $
) Suppose for reductio that
$\Rightarrow $
) Suppose for reductio that
![]() $\square \neg B\vec {\alpha }$
and
$\square \neg B\vec {\alpha }$
and
![]() $\mathrm {is} \alpha _i=n_i$
, but that
$\mathrm {is} \alpha _i=n_i$
, but that
![]() $\neg T(\square \neg B,\vec {n})$
. By the definition of T, there are some
$\neg T(\square \neg B,\vec {n})$
. By the definition of T, there are some
![]() $m_i\succeq n_i$
such that
$m_i\succeq n_i$
such that
![]() $T(B,\vec {m})$
. But
$T(B,\vec {m})$
. But
![]() $\lozenge \bigwedge _i \mathrm {is} \alpha _i=m_i$
, so by i.h.
$\lozenge \bigwedge _i \mathrm {is} \alpha _i=m_i$
, so by i.h.
![]() $\lozenge B\vec {\alpha }$
, a contradiction.
$\lozenge B\vec {\alpha }$
, a contradiction.
(
![]() $\Leftarrow $
) Suppose
$\Leftarrow $
) Suppose
![]() $\neg \square \neg B\vec {\alpha }$
, i.e.,
$\neg \square \neg B\vec {\alpha }$
, i.e.,
![]() $\lozenge B\vec {\alpha }$
, and let
$\lozenge B\vec {\alpha }$
, and let
![]() $\mathrm {is} \alpha _i=n_i$
. It follows that
$\mathrm {is} \alpha _i=n_i$
. It follows that
![]() $\lozenge \exists m_1\succeq n_1 \dots \exists m_k \succeq n_k (\bigwedge _i \mathrm {is} \alpha _i=m_i \wedge B\vec {\alpha }))$
. From i.h. this gives
$\lozenge \exists m_1\succeq n_1 \dots \exists m_k \succeq n_k (\bigwedge _i \mathrm {is} \alpha _i=m_i \wedge B\vec {\alpha }))$
. From i.h. this gives
![]() $\lozenge \exists m_1\succeq n_1 \dots \exists m_k \succeq n_k (\bigwedge _i \mathrm {is} \alpha _i=m_i \wedge T(B,\vec {m}))$
, so it is not the case that
$\lozenge \exists m_1\succeq n_1 \dots \exists m_k \succeq n_k (\bigwedge _i \mathrm {is} \alpha _i=m_i \wedge T(B,\vec {m}))$
, so it is not the case that
![]() $\forall m_1\succeq n_1 \dots \forall m_k\succeq n_k \neg T(B,\vec {m})$
. That is,
$\forall m_1\succeq n_1 \dots \forall m_k\succeq n_k \neg T(B,\vec {m})$
. That is,
![]() $\neg T(A,n)$
, as required.
$\neg T(A,n)$
, as required.
Case 4: A is
![]() $\square (B\rightarrow C)$
.
$\square (B\rightarrow C)$
.
(
![]() $\Rightarrow $
) Suppose
$\Rightarrow $
) Suppose
![]() $\square (B\vec {\alpha } \rightarrow C\vec {\alpha })$
and let
$\square (B\vec {\alpha } \rightarrow C\vec {\alpha })$
and let
![]() $\mathrm {is} \alpha _i=n_i$
. Let
$\mathrm {is} \alpha _i=n_i$
. Let
![]() $m_1\succeq n_1,\dots ,m_k\succeq n_k$
be arbitrary, and suppose
$m_1\succeq n_1,\dots ,m_k\succeq n_k$
be arbitrary, and suppose
![]() $T(B,\vec {m})$
. We know
$T(B,\vec {m})$
. We know
![]() $\lozenge \bigwedge _i \mathrm {is} \alpha _i=m_i$
, so by i.h.
$\lozenge \bigwedge _i \mathrm {is} \alpha _i=m_i$
, so by i.h.
![]() $\lozenge (\mathrm {is} \alpha _i=m_i \wedge B\vec {\alpha })$
. Thus
$\lozenge (\mathrm {is} \alpha _i=m_i \wedge B\vec {\alpha })$
. Thus
![]() $\lozenge (\mathrm {is} \alpha _i=m_i \wedge C\vec {\alpha })$
, and by i.h.
$\lozenge (\mathrm {is} \alpha _i=m_i \wedge C\vec {\alpha })$
, and by i.h.
![]() $T(C,\vec {m})$
. So
$T(C,\vec {m})$
. So
![]() $\forall m_1\succeq n_1,\dots ,m_k\succeq n_k (T(B,\vec {m}) \rightarrow T(C,\vec {m}))$
.
$\forall m_1\succeq n_1,\dots ,m_k\succeq n_k (T(B,\vec {m}) \rightarrow T(C,\vec {m}))$
.
(
![]() $\Leftarrow $
) Suppose
$\Leftarrow $
) Suppose
![]() $\mathrm {is} \alpha _i=n_i$
and
$\mathrm {is} \alpha _i=n_i$
and
![]() $\forall m_1\succeq n_1,\dots ,m_k\succeq n_k (T(B,\vec {m}) \rightarrow T(C,\vec {m}))$
. Now,
$\forall m_1\succeq n_1,\dots ,m_k\succeq n_k (T(B,\vec {m}) \rightarrow T(C,\vec {m}))$
. Now,
![]() $\square \exists m_1\succeq n_1,\dots ,m_k\succeq n_k \bigwedge _i \mathrm {is} \alpha _i=m_i$
. So, necessarily: if
$\square \exists m_1\succeq n_1,\dots ,m_k\succeq n_k \bigwedge _i \mathrm {is} \alpha _i=m_i$
. So, necessarily: if
![]() $B\vec {\alpha }$
, then by i.h.
$B\vec {\alpha }$
, then by i.h.
![]() $T(B,\vec {m})$
, from which our initial assumption gives
$T(B,\vec {m})$
, from which our initial assumption gives
![]() $T(C,\vec {m})$
, and then by i.h.
$T(C,\vec {m})$
, and then by i.h.
![]() $C\vec {\alpha }$
. Thus,
$C\vec {\alpha }$
. Thus,
![]() $\square (B\vec {\alpha } \rightarrow C\vec {\alpha })$
.
$\square (B\vec {\alpha } \rightarrow C\vec {\alpha })$
.
Case 5: A is
![]() $\square \forall x B$
. Both directions can be proved simultaneously. By the i.h. we have
$\square \forall x B$
. Both directions can be proved simultaneously. By the i.h. we have
 $$ \begin{align*}\square \forall x \left( B\vec{\alpha} \leftrightarrow \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow T(B,\vec{n}) \right) \right).\end{align*} $$
$$ \begin{align*}\square \forall x \left( B\vec{\alpha} \leftrightarrow \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow T(B,\vec{n}) \right) \right).\end{align*} $$
This gives us
 $$ \begin{align*}\square \forall x B\vec{\alpha} \leftrightarrow \square \forall x \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow T(B,\vec{n}) \right),\end{align*} $$
$$ \begin{align*}\square \forall x B\vec{\alpha} \leftrightarrow \square \forall x \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow T(B,\vec{n}) \right),\end{align*} $$
which entails
 $$ \begin{align*}\square \forall x B\vec{\alpha} \leftrightarrow \square \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall x T(B,\vec{n}) \right) .\end{align*} $$
$$ \begin{align*}\square \forall x B\vec{\alpha} \leftrightarrow \square \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall x T(B,\vec{n}) \right) .\end{align*} $$
Now, if
![]() $\bigwedge _i \mathrm {is} \alpha _i=n_i$
, then
$\bigwedge _i \mathrm {is} \alpha _i=n_i$
, then
![]() $\square \exists m_1\succeq n_1 \dots \exists m_k\succeq n_k \bigwedge _i \mathrm {is} \alpha_i=m_i$
and also
$\square \exists m_1\succeq n_1 \dots \exists m_k\succeq n_k \bigwedge _i \mathrm {is} \alpha_i=m_i$
and also
![]() $\forall m_1\succeq n_1 \dots \forall m_k\succeq n_k \lozenge \bigwedge _i \mathrm {is} \alpha _i=m_i$
. This gives
$\forall m_1\succeq n_1 \dots \forall m_k\succeq n_k \lozenge \bigwedge _i \mathrm {is} \alpha _i=m_i$
. This gives
 $$ \begin{align*}\square \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall x T(B,\vec{n}) \right) \leftrightarrow \square \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} \forall x T(B,\vec{m}) \right).\end{align*} $$
$$ \begin{align*}\square \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall x T(B,\vec{n}) \right) \leftrightarrow \square \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} \forall x T(B,\vec{m}) \right).\end{align*} $$
Finally, note that
 $$ \begin{align*}&\square \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} \forall x T(B,\vec{m}) \right)\\ & \quad \leftrightarrow \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} \forall x T(B,\vec{m}) \right).\end{align*} $$
$$ \begin{align*}&\square \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} \forall x T(B,\vec{m}) \right)\\ & \quad \leftrightarrow \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} \forall x T(B,\vec{m}) \right).\end{align*} $$
The left-to-right part is trivial. For the right-to-left, consider three cases. First, if
![]() $\vec {n}$
is incompatible with
$\vec {n}$
is incompatible with
![]() $\overrightarrow {\mathrm {is} \alpha }$
, then
$\overrightarrow {\mathrm {is} \alpha }$
, then
![]() $\bigwedge _i \mathrm {is} \alpha _i=n_i$
is necessarily false. Second, if
$\bigwedge _i \mathrm {is} \alpha _i=n_i$
is necessarily false. Second, if
![]() $\vec {n}=\overrightarrow {\mathrm {is} \alpha }$
, then by Lemma 8.10,
$\vec {n}=\overrightarrow {\mathrm {is} \alpha }$
, then by Lemma 8.10,
![]() $\forall \vec {m} \succeq \vec {n} \forall x T(B,\vec {m})$
is true and hence by stability necessarily true. Third, if
$\forall \vec {m} \succeq \vec {n} \forall x T(B,\vec {m})$
is true and hence by stability necessarily true. Third, if
![]() $\vec {n}\succeq \overrightarrow {\mathrm {is} \alpha }$
, then from the fact that
$\vec {n}\succeq \overrightarrow {\mathrm {is} \alpha }$
, then from the fact that
![]() $\forall m \succeq \overrightarrow {\mathrm {is} \alpha } \forall x T(B,\vec {m})$
it also follows that
$\forall m \succeq \overrightarrow {\mathrm {is} \alpha } \forall x T(B,\vec {m})$
it also follows that
![]() $\forall \vec {m}\succeq \forall \vec {n} \forall x T(B,x)$
is true, and hence necessarily true. Putting this all together, we have our desired equivalence:
$\forall \vec {m}\succeq \forall \vec {n} \forall x T(B,x)$
is true, and hence necessarily true. Putting this all together, we have our desired equivalence:
 $$ \begin{align*}\square \forall x B\alpha \leftrightarrow \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m} \succeq \vec{n} \forall x T(B,\vec{m}) \right) .\end{align*} $$
$$ \begin{align*}\square \forall x B\alpha \leftrightarrow \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m} \succeq \vec{n} \forall x T(B,\vec{m}) \right) .\end{align*} $$
Case 6: A is
![]() $\mathcal {I}\exists x B$
.
$\mathcal {I}\exists x B$
.
(
![]() $\Rightarrow $
) Suppose
$\Rightarrow $
) Suppose
![]() $\mathcal {I}\exists x B\vec {\alpha }$
and that
$\mathcal {I}\exists x B\vec {\alpha }$
and that
![]() $\mathrm {is} \alpha _i=n_i$
. By i.h. we have
$\mathrm {is} \alpha _i=n_i$
. By i.h. we have
![]() $ \square \forall x [ B\vec {\alpha } \rightarrow \forall \vec {m} (\bigwedge _i \mathrm {is} \alpha _i = m_i \rightarrow T(B,\vec {m}))]$
. This entails
$ \square \forall x [ B\vec {\alpha } \rightarrow \forall \vec {m} (\bigwedge _i \mathrm {is} \alpha _i = m_i \rightarrow T(B,\vec {m}))]$
. This entails
![]() $\mathcal {I}\exists x B\alpha \rightarrow \mathcal {I} \exists x \forall \vec {m} (\bigwedge _i \mathrm {is} \alpha _i = m_i \rightarrow T(B,\vec {m}))$
, and so by modus ponens
$\mathcal {I}\exists x B\alpha \rightarrow \mathcal {I} \exists x \forall \vec {m} (\bigwedge _i \mathrm {is} \alpha _i = m_i \rightarrow T(B,\vec {m}))$
, and so by modus ponens
![]() $\mathcal {I} \exists x \forall \vec {m} (\bigwedge _i \mathrm {is} \alpha _i = m_i \rightarrow T(B,\vec {m}))$
. Since x is not free in
$\mathcal {I} \exists x \forall \vec {m} (\bigwedge _i \mathrm {is} \alpha _i = m_i \rightarrow T(B,\vec {m}))$
. Since x is not free in
![]() $\mathrm {is} \alpha _i=m_i$
, this entails
$\mathrm {is} \alpha _i=m_i$
, this entails
![]() $\mathcal {I} \forall \vec {m} (\bigwedge _i \mathrm {is} \alpha _i = m_i \rightarrow \exists x T(B,\vec {m}))$
. Now suppose for reductio that
$\mathcal {I} \forall \vec {m} (\bigwedge _i \mathrm {is} \alpha _i = m_i \rightarrow \exists x T(B,\vec {m}))$
. Now suppose for reductio that
![]() $\exists g_1\in n_1 \dots \exists g_k\in n_k \forall y_1 \dots \forall y_k \neg \exists x T(B,\overline {g_1}(y_1),\dots ,\overline {g_k}(y_k))$
. Then as long as each
$\exists g_1\in n_1 \dots \exists g_k\in n_k \forall y_1 \dots \forall y_k \neg \exists x T(B,\overline {g_1}(y_1),\dots ,\overline {g_k}(y_k))$
. Then as long as each
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $g_i$
agree—that is, as long as for some
$g_i$
agree—that is, as long as for some
![]() $y_1,\dots ,y_k$
,
$y_1,\dots ,y_k$
,
![]() $\bigwedge _i \mathrm {is} \alpha _i=\overline {g_i}(y_i)$
—it will not be the case that
$\bigwedge _i \mathrm {is} \alpha _i=\overline {g_i}(y_i)$
—it will not be the case that
![]() $\exists x T(B,\mathrm {is} \alpha _1,\dots ,\mathrm {is} \alpha _k)$
. But since all the
$\exists x T(B,\mathrm {is} \alpha _1,\dots ,\mathrm {is} \alpha _k)$
. But since all the
![]() $\alpha _i$
’s and
$\alpha _i$
’s and
![]() $g_i$
’s agree so far, it is not inevitable that they ever disagree. Thus,
$g_i$
’s agree so far, it is not inevitable that they ever disagree. Thus,
![]() $\neg \mathcal {I} \forall \vec {m} (\bigwedge _i \mathrm {is} \alpha _i=m_i \rightarrow \exists x T(B,\vec {m}) )$
, which is a contradiction.
$\neg \mathcal {I} \forall \vec {m} (\bigwedge _i \mathrm {is} \alpha _i=m_i \rightarrow \exists x T(B,\vec {m}) )$
, which is a contradiction.
(
![]() $\Leftarrow $
) This is exactly the same as “
$\Leftarrow $
) This is exactly the same as “
![]() $\Leftarrow $
” in Case 2, except that we work with the formula
$\Leftarrow $
” in Case 2, except that we work with the formula
![]() $C(\vec {m}) :\leftrightarrow \vec {n}\preceq \vec {m} \neg \exists x T(B,n^\frown m) $
.
$C(\vec {m}) :\leftrightarrow \vec {n}\preceq \vec {m} \neg \exists x T(B,n^\frown m) $
.
Cases 7 and 8: A is
![]() $\square \forall f B$
or
$\square \forall f B$
or
![]() $\mathcal {I}\exists f B$
. These are exactly the same as Cases 5 and 6.
$\mathcal {I}\exists f B$
. These are exactly the same as Cases 5 and 6.
Case 9: A is
![]() $\square \forall \gamma B(\vec {\alpha },\gamma )$
. First observe that by Proposition 8.7,
$\square \forall \gamma B(\vec {\alpha },\gamma )$
. First observe that by Proposition 8.7,
![]() $\square \forall \gamma B(\vec {\alpha },\gamma )$
is equivalent to
$\square \forall \gamma B(\vec {\alpha },\gamma )$
is equivalent to
![]() $\square \bigwedge _i B^\gamma _{\alpha _i}(\vec {\alpha }) \wedge \square \forall \gamma (\bigwedge _i \neg \square \forall x \gamma (x)\simeq \alpha _i(x) \rightarrow B(\vec {\alpha },\gamma )$
. I will treat the two conjunctions as separate cases.
$\square \bigwedge _i B^\gamma _{\alpha _i}(\vec {\alpha }) \wedge \square \forall \gamma (\bigwedge _i \neg \square \forall x \gamma (x)\simeq \alpha _i(x) \rightarrow B(\vec {\alpha },\gamma )$
. I will treat the two conjunctions as separate cases.
By i.h. we know that for each i,
![]() $B^\gamma _{\alpha _i}(\vec {\alpha }) \leftrightarrow \forall \vec {n} \left ( \bigwedge _i\mathrm {is} \alpha _i=n_i \rightarrow T(B^\gamma _{\alpha _i},\vec {n}) \right )$
. And hence by Lemma 8.10,
$B^\gamma _{\alpha _i}(\vec {\alpha }) \leftrightarrow \forall \vec {n} \left ( \bigwedge _i\mathrm {is} \alpha _i=n_i \rightarrow T(B^\gamma _{\alpha _i},\vec {n}) \right )$
. And hence by Lemma 8.10,
![]() $B^\gamma _{\alpha _i}(\vec {\alpha }) \leftrightarrow \forall \vec {n} \left ( \bigwedge _i\mathrm {is} \alpha _i=n_i \rightarrow \forall \vec {m}\succeq \vec {n} T(B^\gamma _{\alpha _i}, \vec {m}) \right )$
. This entails
$B^\gamma _{\alpha _i}(\vec {\alpha }) \leftrightarrow \forall \vec {n} \left ( \bigwedge _i\mathrm {is} \alpha _i=n_i \rightarrow \forall \vec {m}\succeq \vec {n} T(B^\gamma _{\alpha _i}, \vec {m}) \right )$
. This entails
 $$ \begin{align*}\square B^\gamma_{\alpha_i}(\vec{\alpha}) \leftrightarrow \square \forall \vec{n} \left( \bigwedge_i\mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} T(B^\gamma_{\alpha_i},\vec{m}) \right).\end{align*} $$
$$ \begin{align*}\square B^\gamma_{\alpha_i}(\vec{\alpha}) \leftrightarrow \square \forall \vec{n} \left( \bigwedge_i\mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} T(B^\gamma_{\alpha_i},\vec{m}) \right).\end{align*} $$
By the argument from Case 5, we know
 $$ \begin{align*}&\square \forall \vec{n} \left( \bigwedge_i\mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} T(B^\gamma_{\alpha_i},\vec{m}) \right)\\ & \quad\qquad \leftrightarrow \forall \vec{n} \left( \bigwedge_i\mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} T(B^\gamma_{\alpha_i},\vec{m}) \right).\end{align*} $$
$$ \begin{align*}&\square \forall \vec{n} \left( \bigwedge_i\mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} T(B^\gamma_{\alpha_i},\vec{m}) \right)\\ & \quad\qquad \leftrightarrow \forall \vec{n} \left( \bigwedge_i\mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} T(B^\gamma_{\alpha_i},\vec{m}) \right).\end{align*} $$
Putting these together gives our result.
Turn now to the other case,
![]() $\square \forall \gamma (\bigwedge _i \neg \square \forall x \gamma (x)\simeq \alpha _i(x) \rightarrow B(\gamma ,\vec {\alpha })$
. From i.h. we know
$\square \forall \gamma (\bigwedge _i \neg \square \forall x \gamma (x)\simeq \alpha _i(x) \rightarrow B(\gamma ,\vec {\alpha })$
. From i.h. we know
 $$ \begin{align*}&\forall \gamma \left( \bigwedge_i \neg\square \forall x \gamma(x)\simeq \alpha_i(x)\right.\\ & \qquad \left.\rightarrow \left( B(\gamma,\vec{\alpha}) \leftrightarrow \forall \vec{n} \forall n_{k+1} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \wedge \mathrm{is} \gamma=n_{k+1} \rightarrow T(B,\vec{n},n_{k+1})\! \right)\! \right)\! \right) \!.\end{align*} $$
$$ \begin{align*}&\forall \gamma \left( \bigwedge_i \neg\square \forall x \gamma(x)\simeq \alpha_i(x)\right.\\ & \qquad \left.\rightarrow \left( B(\gamma,\vec{\alpha}) \leftrightarrow \forall \vec{n} \forall n_{k+1} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \wedge \mathrm{is} \gamma=n_{k+1} \rightarrow T(B,\vec{n},n_{k+1})\! \right)\! \right)\! \right) \!.\end{align*} $$
This gives us:
 $$ \begin{align*} &\square \forall \gamma \left( \bigwedge_i \neg\square \forall x \gamma(x)\simeq \alpha_i(x) \rightarrow B(\vec{\alpha},\gamma) \right) \leftrightarrow \\& \quad \square \forall \gamma \left( \bigwedge_i \neg\square \forall x \gamma(x) \simeq \alpha_i(x) \rightarrow \ \forall \vec{m} \forall m_{k+1}\right.\\& \qquad\qquad \left.\left( \bigwedge_i \mathrm{is} \alpha_i=m_i \wedge \mathrm{is} \gamma=m_{k+1} \rightarrow T(B,\vec{m},m_{k+1}) \right) \right). \end{align*} $$
$$ \begin{align*} &\square \forall \gamma \left( \bigwedge_i \neg\square \forall x \gamma(x)\simeq \alpha_i(x) \rightarrow B(\vec{\alpha},\gamma) \right) \leftrightarrow \\& \quad \square \forall \gamma \left( \bigwedge_i \neg\square \forall x \gamma(x) \simeq \alpha_i(x) \rightarrow \ \forall \vec{m} \forall m_{k+1}\right.\\& \qquad\qquad \left.\left( \bigwedge_i \mathrm{is} \alpha_i=m_i \wedge \mathrm{is} \gamma=m_{k+1} \rightarrow T(B,\vec{m},m_{k+1}) \right) \right). \end{align*} $$
For every
![]() $m_{k+1}$
it is possible that there is a
$m_{k+1}$
it is possible that there is a
![]() $\gamma $
distinct from all the
$\gamma $
distinct from all the
![]() $\alpha $
’s with
$\alpha $
’s with
![]() $\mathrm {is} \gamma =m_{k+1}$
. (This follows from S4 and S9.) Conversely, for every
$\mathrm {is} \gamma =m_{k+1}$
. (This follows from S4 and S9.) Conversely, for every
![]() $\gamma $
there will necessarily be some
$\gamma $
there will necessarily be some
![]() $m_{k+1}$
that is its initial segment. And moreover, if
$m_{k+1}$
that is its initial segment. And moreover, if
![]() $\mathrm {is} \alpha _i=n_i$
, then necessarily there is some
$\mathrm {is} \alpha _i=n_i$
, then necessarily there is some
![]() $\vec {m}\succeq \vec {n}$
such that
$\vec {m}\succeq \vec {n}$
such that
![]() $\mathrm {is} \alpha _i=n_i$
; and for each
$\mathrm {is} \alpha _i=n_i$
; and for each
![]() $\vec {m}\succeq \vec {n}$
this is possible. From all this we may infer:
$\vec {m}\succeq \vec {n}$
this is possible. From all this we may infer:
 $$ \begin{align*}&\square \forall \gamma \left( \bigwedge_i \neg\square \forall x \gamma(x) \simeq \alpha_i(x) \rightarrow B(\vec{\alpha},\gamma) \right)\\ & \quad \leftrightarrow \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} \forall m_{k+1} T(B,\vec{m},m_{k+1}) \right).\end{align*} $$
$$ \begin{align*}&\square \forall \gamma \left( \bigwedge_i \neg\square \forall x \gamma(x) \simeq \alpha_i(x) \rightarrow B(\vec{\alpha},\gamma) \right)\\ & \quad \leftrightarrow \forall \vec{n} \left( \bigwedge_i \mathrm{is} \alpha_i=n_i \rightarrow \forall \vec{m}\succeq \vec{n} \forall m_{k+1} T(B,\vec{m},m_{k+1}) \right).\end{align*} $$
Putting these two cases together gives us the desired result:
 $$ \begin{align*}\square \forall \gamma B(\vec{\alpha},\gamma) \leftrightarrow \forall \vec{m}\succeq \vec{n} \left( \bigwedge_{1\leq i \leq k} T(B^\gamma_{\alpha_i},\vec{m}) \wedge \forall m_{k+1} T(B,\vec{m},m_{k+1}) \right).\end{align*} $$
$$ \begin{align*}\square \forall \gamma B(\vec{\alpha},\gamma) \leftrightarrow \forall \vec{m}\succeq \vec{n} \left( \bigwedge_{1\leq i \leq k} T(B^\gamma_{\alpha_i},\vec{m}) \wedge \forall m_{k+1} T(B,\vec{m},m_{k+1}) \right).\end{align*} $$
Case 10: A is
![]() $\mathcal {I}\exists \gamma B$
.
$\mathcal {I}\exists \gamma B$
.
(
![]() $\Rightarrow $
) Suppose
$\Rightarrow $
) Suppose
![]() $\mathcal {I}\exists \gamma B(\vec {\alpha },\gamma )$
and let
$\mathcal {I}\exists \gamma B(\vec {\alpha },\gamma )$
and let
![]() $\mathrm {is} \alpha _i=n_i$
. Then for every
$\mathrm {is} \alpha _i=n_i$
. Then for every
![]() $\vec {g}\in \vec {n}$
it is not inevitable that any
$\vec {g}\in \vec {n}$
it is not inevitable that any
![]() $g_i$
and
$g_i$
and
![]() $\alpha _i$
disagree. So by Proposition 4.2, we have
$\alpha _i$
disagree. So by Proposition 4.2, we have
![]() $\lozenge \exists \vec {y} (\bigwedge _i \mathrm {is} \alpha _i=\overline {g_i}(y_i) \wedge \exists \gamma B)$
. Again we consider two possible ranges of values for the witness
$\lozenge \exists \vec {y} (\bigwedge _i \mathrm {is} \alpha _i=\overline {g_i}(y_i) \wedge \exists \gamma B)$
. Again we consider two possible ranges of values for the witness
![]() $\gamma $
: either for some i,
$\gamma $
: either for some i,
![]() $\square \forall x \gamma (x)\simeq \alpha _i(x)$
, or not.
$\square \forall x \gamma (x)\simeq \alpha _i(x)$
, or not.
In the first case, by i.h. we have
![]() $\lozenge \exists \vec {y} (\bigwedge _i \mathrm {is} \alpha _i=\overline {g_i}(y_i) \wedge T(B^\gamma _{\alpha _i},\overline {g_1}(y_1),\dots , \overline {g_k}(y_k))$
, from which we get
$\lozenge \exists \vec {y} (\bigwedge _i \mathrm {is} \alpha _i=\overline {g_i}(y_i) \wedge T(B^\gamma _{\alpha _i},\overline {g_1}(y_1),\dots , \overline {g_k}(y_k))$
, from which we get
![]() $\exists \vec {y} \, T(B^\gamma _{\alpha _i},\overline {g_1}(y_1),\dots ,\overline {g_k}(y_k))$
.
$\exists \vec {y} \, T(B^\gamma _{\alpha _i},\overline {g_1}(y_1),\dots ,\overline {g_k}(y_k))$
.
In the second case, we know from i.h. that
 $$ \begin{align*} &\exists \gamma \left( \bigwedge_i \neg\square \forall x \gamma(x)\simeq\alpha_i(x) \wedge B \right) \\& \rightarrow \exists \gamma \left( \bigwedge_i \neg\square\forall x \gamma(x)\simeq\alpha_i(x) \wedge \forall \vec{m} \forall m_{k+1}\right.\\& \qquad\qquad \left.\left( \bigwedge_i \mathrm{is} \alpha_i=m_i \wedge \mathrm{is}\gamma=m_{k+1} \rightarrow T(B,\vec{m},m_{k+1}) \right) \right). \end{align*} $$
$$ \begin{align*} &\exists \gamma \left( \bigwedge_i \neg\square \forall x \gamma(x)\simeq\alpha_i(x) \wedge B \right) \\& \rightarrow \exists \gamma \left( \bigwedge_i \neg\square\forall x \gamma(x)\simeq\alpha_i(x) \wedge \forall \vec{m} \forall m_{k+1}\right.\\& \qquad\qquad \left.\left( \bigwedge_i \mathrm{is} \alpha_i=m_i \wedge \mathrm{is}\gamma=m_{k+1} \rightarrow T(B,\vec{m},m_{k+1}) \right) \right). \end{align*} $$
Now, necessarily for all
![]() $\gamma $
there is some
$\gamma $
there is some
![]() $m_{k+1}$
that is its initial segment, so this simplifies to
$m_{k+1}$
that is its initial segment, so this simplifies to
 $$ \begin{align*}\exists \gamma \left( \bigwedge_i \neg\square \forall x \gamma(x)\simeq\alpha_i(x) \wedge B \right) \rightarrow \forall \vec{m} \left( \bigwedge_i \mathrm{is} \alpha_i=m_i \rightarrow \exists m_{k+1} T(B,\vec{m},m_{k+1}) \right).\end{align*} $$
$$ \begin{align*}\exists \gamma \left( \bigwedge_i \neg\square \forall x \gamma(x)\simeq\alpha_i(x) \wedge B \right) \rightarrow \forall \vec{m} \left( \bigwedge_i \mathrm{is} \alpha_i=m_i \rightarrow \exists m_{k+1} T(B,\vec{m},m_{k+1}) \right).\end{align*} $$
Recall we already had
![]() $\lozenge \exists \vec {y} (\bigwedge _i \mathrm {is} \alpha _i=\overline {g_i}(y_i) \wedge \exists \gamma B)$
, so this gives us
$\lozenge \exists \vec {y} (\bigwedge _i \mathrm {is} \alpha _i=\overline {g_i}(y_i) \wedge \exists \gamma B)$
, so this gives us
![]() $\exists \vec {y}\exists m T(B,\overrightarrow {\overline {g}(y)},m_{k+1})$
.
$\exists \vec {y}\exists m T(B,\overrightarrow {\overline {g}(y)},m_{k+1})$
.
Putting these two cases together, and since
![]() $\vec {g}\in \vec {n}$
was arbitrary, we have our desired conclusion:
$\vec {g}\in \vec {n}$
was arbitrary, we have our desired conclusion:
 $$ \begin{align*}\forall \vec{g}\in \vec{n} \exists \vec{y} \left( \bigvee_i T(B^\gamma_{\alpha_i},\overline{g_1}(y_1),\dots,\overline{g_k}(y_k)) \vee \exists m_{k+1} T(B,\overline{g_1}(y_1),\dots,\overline{g_k}(y_k),m_{k+1}) \right).\end{align*} $$
$$ \begin{align*}\forall \vec{g}\in \vec{n} \exists \vec{y} \left( \bigvee_i T(B^\gamma_{\alpha_i},\overline{g_1}(y_1),\dots,\overline{g_k}(y_k)) \vee \exists m_{k+1} T(B,\overline{g_1}(y_1),\dots,\overline{g_k}(y_k),m_{k+1}) \right).\end{align*} $$
(
![]() $\Leftarrow $
) Suppose
$\Leftarrow $
) Suppose
![]() $\mathrm {is} \alpha _i=n_i$
and that
$\mathrm {is} \alpha _i=n_i$
and that
 $$ \begin{align*}\forall \vec{g}\in \vec{n} \exists \vec{y} \left( \bigvee_i T(B^\gamma_{\alpha_i},\overline{g_1}(y_1),\dots,\overline{g_k}(y_k)) \vee \exists m_{k+1} T(B,\overline{g_1}(y_1),\dots,\overline{g_k}(y_k),m_{k+1}) \right).\end{align*} $$
$$ \begin{align*}\forall \vec{g}\in \vec{n} \exists \vec{y} \left( \bigvee_i T(B^\gamma_{\alpha_i},\overline{g_1}(y_1),\dots,\overline{g_k}(y_k)) \vee \exists m_{k+1} T(B,\overline{g_1}(y_1),\dots,\overline{g_k}(y_k),m_{k+1}) \right).\end{align*} $$
Let
![]() $C(\vec {m})$
be the formula
$C(\vec {m})$
be the formula
![]() $\vec {m}\succeq \vec {n} \wedge \bigwedge _i \neg T(B^\gamma _{\alpha _i},\vec {m}) \wedge \neg \exists m_{k+1} T(B,\vec {m},m_{k+1}) $
. Clearly C is quasi-treelike and by assumption it is well-founded, so inevitably
$\vec {m}\succeq \vec {n} \wedge \bigwedge _i \neg T(B^\gamma _{\alpha _i},\vec {m}) \wedge \neg \exists m_{k+1} T(B,\vec {m},m_{k+1}) $
. Clearly C is quasi-treelike and by assumption it is well-founded, so inevitably
![]() $\vec {\alpha }$
will leave C. If
$\vec {\alpha }$
will leave C. If
![]() $\vec {\alpha }$
leaves C by satisfying one of the disjuncts
$\vec {\alpha }$
leaves C by satisfying one of the disjuncts
![]() $T(B^\gamma _{\alpha _i},\overrightarrow {\mathrm {is} \alpha })$
, then by i.h. we have
$T(B^\gamma _{\alpha _i},\overrightarrow {\mathrm {is} \alpha })$
, then by i.h. we have
![]() $B^\gamma _{\alpha _i}$
and hence
$B^\gamma _{\alpha _i}$
and hence
![]() $\exists \gamma B$
. On the other hand, if
$\exists \gamma B$
. On the other hand, if
![]() $\vec {\alpha }$
leave C by satisfying
$\vec {\alpha }$
leave C by satisfying
![]() $\exists m_{k+1} T(B,\overrightarrow {\mathrm {is} \alpha },m_{k+1})$
, then we cannot necessarily infer
$\exists m_{k+1} T(B,\overrightarrow {\mathrm {is} \alpha },m_{k+1})$
, then we cannot necessarily infer
![]() $\exists \gamma B$
because there may not be a
$\exists \gamma B$
because there may not be a
![]() $\gamma $
with an initial segment identical to (or extending, by Lemma 8.10) the witness
$\gamma $
with an initial segment identical to (or extending, by Lemma 8.10) the witness
![]() $m_{k+1}$
. What we do know, however, is that there will inevitably be some such
$m_{k+1}$
. What we do know, however, is that there will inevitably be some such
![]() $\gamma $
. So if
$\gamma $
. So if
![]() $\vec {\alpha }$
leaves C, then it follows that
$\vec {\alpha }$
leaves C, then it follows that
![]() $\mathcal {I}\exists \gamma B$
. So, since it is inevitable that
$\mathcal {I}\exists \gamma B$
. So, since it is inevitable that
![]() $\vec {\alpha }$
leaves C, we infer
$\vec {\alpha }$
leaves C, we infer
![]() $\mathcal {I}\exists \gamma B$
.
$\mathcal {I}\exists \gamma B$
.
C Proofs for the conservation theorem
This appendix includes proofs of Theorems 9.6 and 9.7.
Theorem 9.6, recall, asserts that every axiom of
![]() $MC_{LS}(Z)$
is forced at every
$MC_{LS}(Z)$
is forced at every
![]() $w\in \mathbb {P}$
.
$w\in \mathbb {P}$
.
Proof of Theorem 9.6
The arithmetic axioms are forced in light of Theorem 9.5, so it suffices to show that every node forces S1–S9. Letting
![]() $w\in \mathbb {P}$
and
$w\in \mathbb {P}$
and
![]() $\sigma $
be arbitrary, we consider each axiom in turn.
$\sigma $
be arbitrary, we consider each axiom in turn.
S1 is
![]() $\exists n \in Seq ~\mathrm {is} \alpha =n$
. This is forced at w just in case for every
$\exists n \in Seq ~\mathrm {is} \alpha =n$
. This is forced at w just in case for every
![]() $\sigma $
there is an
$\sigma $
there is an
![]() $n\in Seq^M$
such that
$n\in Seq^M$
such that
![]() $w,\sigma \Vdash \mathrm {is} \alpha =n$
. Letting
$w,\sigma \Vdash \mathrm {is} \alpha =n$
. Letting
![]() $n=w(\sigma (\alpha ))$
, this holds by the definition of forcing.
$n=w(\sigma (\alpha ))$
, this holds by the definition of forcing.
S2 is
![]() $\square \forall x \mathcal {I} \exists y \alpha (x)=y$
. Letting
$\square \forall x \mathcal {I} \exists y \alpha (x)=y$
. Letting
![]() $u\sqsupseteq w$
be arbitrary, we need to show that for every x,
$u\sqsupseteq w$
be arbitrary, we need to show that for every x,
![]() $u,\sigma \Vdash \mathcal {I} \exists y \alpha (x)=y$
. Let I be an arbitrary index set including
$u,\sigma \Vdash \mathcal {I} \exists y \alpha (x)=y$
. Let I be an arbitrary index set including
![]() $\sigma (\alpha )$
, let
$\sigma (\alpha )$
, let
![]() $f_i\in u(i)$
be arbitrary, and let C be an arbitrary
$f_i\in u(i)$
be arbitrary, and let C be an arbitrary
![]() $[f_i]_I$
-chain above u. By the definition of an
$[f_i]_I$
-chain above u. By the definition of an
![]() $[f_i]_I$
-chain, there will be some
$[f_i]_I$
-chain, there will be some
![]() $v\in C$
such that
$v\in C$
such that
![]() $v(\sigma (\alpha ))\succeq \overline {f_{\sigma (\alpha )}}(x)$
, so
$v(\sigma (\alpha ))\succeq \overline {f_{\sigma (\alpha )}}(x)$
, so
![]() $v,\sigma \Vdash \exists y \alpha (x)=y$
. Hence
$v,\sigma \Vdash \exists y \alpha (x)=y$
. Hence
![]() $w,\sigma \Vdash \square \forall x \mathcal {I} \exists y \alpha (x)=y$
.
$w,\sigma \Vdash \square \forall x \mathcal {I} \exists y \alpha (x)=y$
.
S3 is
![]() $\square \forall x \forall y (\alpha (x)=y\rightarrow \square \alpha (x)=y)$
. Let
$\square \forall x \forall y (\alpha (x)=y\rightarrow \square \alpha (x)=y)$
. Let
![]() $u\sqsupseteq w$
be arbitrary, we need to show that for all x and y,
$u\sqsupseteq w$
be arbitrary, we need to show that for all x and y,
![]() $u,\sigma \Vdash (\alpha (x)=y\rightarrow \square \alpha (x)=y)$
. Suppose
$u,\sigma \Vdash (\alpha (x)=y\rightarrow \square \alpha (x)=y)$
. Suppose
![]() $u,\sigma \Vdash \alpha (x)=y$
. Then
$u,\sigma \Vdash \alpha (x)=y$
. Then
![]() $u(\sigma (\alpha ))(x)=y$
. For any
$u(\sigma (\alpha ))(x)=y$
. For any
![]() $v\sqsupseteq u$
,
$v\sqsupseteq u$
,
![]() $v(\sigma (\alpha ))$
will be an extension of
$v(\sigma (\alpha ))$
will be an extension of
![]() $u(\sigma (\alpha ))$
, so
$u(\sigma (\alpha ))$
, so
![]() $v,\sigma \Vdash \alpha (x)=y$
, and hence
$v,\sigma \Vdash \alpha (x)=y$
, and hence
![]() $u,\sigma \Vdash \square \alpha (x)=y$
.
$u,\sigma \Vdash \square \alpha (x)=y$
.
S4 is
![]() $\square \exists \alpha \forall x \forall y \alpha (x)\neq y$
. Letting
$\square \exists \alpha \forall x \forall y \alpha (x)\neq y$
. Letting
![]() $u\sqsupseteq w$
be arbitrary, we need to show that there is some i such that for all x and y,
$u\sqsupseteq w$
be arbitrary, we need to show that there is some i such that for all x and y,
![]() $u,\sigma [\alpha \mapsto i] \Vdash \alpha (x)\neq y$
. By the definition of
$u,\sigma [\alpha \mapsto i] \Vdash \alpha (x)\neq y$
. By the definition of
![]() $\mathbb {P}$
, there will be some i such that
$\mathbb {P}$
, there will be some i such that
![]() $u(i)=0$
; so
$u(i)=0$
; so
![]() $\sigma [\alpha \mapsto i]$
assigns the empty sequence to
$\sigma [\alpha \mapsto i]$
assigns the empty sequence to
![]() $\alpha $
at u. Thus for all x and y,
$\alpha $
at u. Thus for all x and y,
![]() $u,\sigma [\alpha \mapsto i] \Vdash \alpha (x)\neq y$
, as required.
$u,\sigma [\alpha \mapsto i] \Vdash \alpha (x)\neq y$
, as required.
S5 is the schema
![]() $qTree^k(A) \wedge WF(<_A) \rightarrow \mathcal {I}\exists z_1\dots \exists z_k (\bigwedge _j \mathrm {is} \alpha _j=z_j \wedge \neg A(\langle z_1,\dots ,z_k\rangle ) )$
. Assume that
$qTree^k(A) \wedge WF(<_A) \rightarrow \mathcal {I}\exists z_1\dots \exists z_k (\bigwedge _j \mathrm {is} \alpha _j=z_j \wedge \neg A(\langle z_1,\dots ,z_k\rangle ) )$
. Assume that
![]() $w \Vdash qTree^k(A) \wedge WF(<_A)$
. Let I and
$w \Vdash qTree^k(A) \wedge WF(<_A)$
. Let I and
![]() $f_i\in w(i)$
be arbitrary, and let C be an arbitrary
$f_i\in w(i)$
be arbitrary, and let C be an arbitrary
![]() $[f_i]_I$
-chain above w. Since
$[f_i]_I$
-chain above w. Since
![]() $WF(<_A)$
, there will be some
$WF(<_A)$
, there will be some
![]() $x_i$
such that
$x_i$
such that
![]() $\neg A\langle f_1(x_1),\dots ,f_k(x_k)\rangle $
. Further, there will be some
$\neg A\langle f_1(x_1),\dots ,f_k(x_k)\rangle $
. Further, there will be some
![]() $u\in C$
such that
$u\in C$
such that
![]() $u(i)\succeq \overline {f_i}(x_i)$
. Letting
$u(i)\succeq \overline {f_i}(x_i)$
. Letting
![]() $z_i=u(i)$
, the definition of forcing ensures
$z_i=u(i)$
, the definition of forcing ensures
![]() $u,\sigma \Vdash \bigwedge _j \mathrm {is} \alpha _j=z_j$
and by the choice of
$u,\sigma \Vdash \bigwedge _j \mathrm {is} \alpha _j=z_j$
and by the choice of
![]() $z_i$
’s we know
$z_i$
’s we know
![]() $u,\sigma \Vdash \neg A(\langle z_1,\dots ,z_k\rangle )$
. So
$u,\sigma \Vdash \neg A(\langle z_1,\dots ,z_k\rangle )$
. So
![]() $w,\sigma \Vdash \mathcal {I} \exists z_1\dots \exists z_k (\bigwedge _j \mathrm {is} \alpha _j=z_j \wedge \neg A(\langle z_1,\dots ,z_k\rangle ) )$
.
$w,\sigma \Vdash \mathcal {I} \exists z_1\dots \exists z_k (\bigwedge _j \mathrm {is} \alpha _j=z_j \wedge \neg A(\langle z_1,\dots ,z_k\rangle ) )$
.
S6 is
![]() $\square \forall n\in Seq \mathcal {I} \exists \alpha (\alpha \in n)$
. Let
$\square \forall n\in Seq \mathcal {I} \exists \alpha (\alpha \in n)$
. Let
![]() $u\sqsupseteq w$
and n be arbitrary. Further, let I and
$u\sqsupseteq w$
and n be arbitrary. Further, let I and
![]() $f_i\in u(i)$
be arbitrary, and let C be an arbitrary
$f_i\in u(i)$
be arbitrary, and let C be an arbitrary
![]() $[f_i]_I$
-chain above u. By the definition of
$[f_i]_I$
-chain above u. By the definition of
![]() $\mathbb {P}$
, there are only finitely many
$\mathbb {P}$
, there are only finitely many
![]() $v\in \mathbb {P}$
such that for no j does
$v\in \mathbb {P}$
such that for no j does
![]() $v(j)=m\succeq n$
. Since there are infinitely many
$v(j)=m\succeq n$
. Since there are infinitely many
![]() $v\in C$
, there must be some
$v\in C$
, there must be some
![]() $v\in C$
such that for some j,
$v\in C$
such that for some j,
![]() $v(j)=m\succeq n$
. Then
$v(j)=m\succeq n$
. Then
![]() $v,\sigma [\alpha \mapsto j] \Vdash \alpha \in n$
.
$v,\sigma [\alpha \mapsto j] \Vdash \alpha \in n$
.
S7 is
![]() $\neg \square \forall x \alpha (x)\simeq \beta (x) \rightarrow \square \neg \square \forall x \alpha (x)\simeq \beta (x) $
. Assume
$\neg \square \forall x \alpha (x)\simeq \beta (x) \rightarrow \square \neg \square \forall x \alpha (x)\simeq \beta (x) $
. Assume
![]() $w,\sigma \nVdash \square \forall x \alpha (x)\simeq \beta (x)$
. So there is some
$w,\sigma \nVdash \square \forall x \alpha (x)\simeq \beta (x)$
. So there is some
![]() $u\sqsupseteq w$
and x such that
$u\sqsupseteq w$
and x such that
![]() $u,\sigma \Vdash (\alpha (x)=\alpha (x)\neq \beta (x)) \vee (\alpha (x)\neq \beta (x)=\beta (x))$
. This obviously can only happen if
$u,\sigma \Vdash (\alpha (x)=\alpha (x)\neq \beta (x)) \vee (\alpha (x)\neq \beta (x)=\beta (x))$
. This obviously can only happen if
![]() $\sigma (\alpha )\neq \sigma (\beta )$
. Now we need to show that for every
$\sigma (\alpha )\neq \sigma (\beta )$
. Now we need to show that for every
![]() $u\sqsupseteq w$
there is a
$u\sqsupseteq w$
there is a
![]() $v\sqsupseteq u$
and an x such that
$v\sqsupseteq u$
and an x such that
![]() $v,\sigma \Vdash (\alpha (x)=\alpha (x)\neq \beta (x)) \vee (\alpha (x)\neq \beta (x)=\beta (x))$
. But since
$v,\sigma \Vdash (\alpha (x)=\alpha (x)\neq \beta (x)) \vee (\alpha (x)\neq \beta (x)=\beta (x))$
. But since
![]() $\sigma (\alpha )\neq \sigma (\beta )$
, this is easily achieved by picking some v such that
$\sigma (\alpha )\neq \sigma (\beta )$
, this is easily achieved by picking some v such that
![]() $v(\sigma (\alpha ))\neq v(\sigma (\beta ))$
.
$v(\sigma (\alpha ))\neq v(\sigma (\beta ))$
.
S8 is the formula:
 $$ \begin{align*} &\bigwedge_{i,j} \neg\square \forall x \alpha_i(x) \simeq \alpha_j(x) \rightarrow \Big( \Big. \neg \exists x_1 \exists y_1 \dots \exists x_k\exists y_k \bigwedge_i (\alpha_i(x_i)=y_i \wedge f_i(x_i)\neq y_i ) \\&\quad\rightarrow \neg \mathcal{I} \exists x_1 \exists y_1 \dots \exists x_k\exists y_k \bigvee_i (\alpha_i(x_i)=y_i \wedge f_i(x_i)\neq y_i ) \Big). \Big. \end{align*} $$
$$ \begin{align*} &\bigwedge_{i,j} \neg\square \forall x \alpha_i(x) \simeq \alpha_j(x) \rightarrow \Big( \Big. \neg \exists x_1 \exists y_1 \dots \exists x_k\exists y_k \bigwedge_i (\alpha_i(x_i)=y_i \wedge f_i(x_i)\neq y_i ) \\&\quad\rightarrow \neg \mathcal{I} \exists x_1 \exists y_1 \dots \exists x_k\exists y_k \bigvee_i (\alpha_i(x_i)=y_i \wedge f_i(x_i)\neq y_i ) \Big). \Big. \end{align*} $$
Assume
![]() $w,\sigma \Vdash \bigwedge _{i,j} \neg \square \forall x \alpha _i(x) \simeq \alpha _j(x)$
and
$w,\sigma \Vdash \bigwedge _{i,j} \neg \square \forall x \alpha _i(x) \simeq \alpha _j(x)$
and
![]() $w,\sigma \Vdash \neg \exists x_1 \exists y_1 \dots \exists x_k\exists y_k \bigwedge _i (\alpha _i(x_i)=y_i \wedge f_i(x_i)\neq y_i )$
. Then we need to show that for some I, there are some
$w,\sigma \Vdash \neg \exists x_1 \exists y_1 \dots \exists x_k\exists y_k \bigwedge _i (\alpha _i(x_i)=y_i \wedge f_i(x_i)\neq y_i )$
. Then we need to show that for some I, there are some
![]() $g_i\in w(i)$
and some
$g_i\in w(i)$
and some
![]() $[g_i]_I$
-chain C such that for all
$[g_i]_I$
-chain C such that for all
![]() $u\in C$
and all
$u\in C$
and all
![]() $x_1,y_1,\dots ,x_k,y_k$
,
$x_1,y_1,\dots ,x_k,y_k$
,
![]() $u,\sigma \Vdash \bigwedge _j( \alpha _j(x_j)=y_j \rightarrow f_j(x_j)=y_j))$
. This is easily accomplished by letting
$u,\sigma \Vdash \bigwedge _j( \alpha _j(x_j)=y_j \rightarrow f_j(x_j)=y_j))$
. This is easily accomplished by letting
![]() $g_i=f_i$
and taking any
$g_i=f_i$
and taking any
![]() $[g_i]_I$
-chain C.
$[g_i]_I$
-chain C.
S9 is the formula:
 $$ \begin{align*} \forall n_1\in Seq \dots \forall n_k\in Seq \Big ( \Big. \bigwedge_{i,j} \neg\square \forall x \alpha_i(x) \simeq \alpha_j(x) \wedge \bigwedge_i \mathrm{is} \alpha_i=n_i \\ \rightarrow \forall m_1\in Seq \dots \forall m_k\in Seq \lozenge\bigwedge_i \mathrm{is} \alpha_i=n_i^\frown m_i \Big ). \Big. \end{align*} $$
$$ \begin{align*} \forall n_1\in Seq \dots \forall n_k\in Seq \Big ( \Big. \bigwedge_{i,j} \neg\square \forall x \alpha_i(x) \simeq \alpha_j(x) \wedge \bigwedge_i \mathrm{is} \alpha_i=n_i \\ \rightarrow \forall m_1\in Seq \dots \forall m_k\in Seq \lozenge\bigwedge_i \mathrm{is} \alpha_i=n_i^\frown m_i \Big ). \Big. \end{align*} $$
Letting
![]() $n_1,\dots ,n_k$
be arbitrary, assume
$n_1,\dots ,n_k$
be arbitrary, assume
![]() $w,\sigma \Vdash \bigwedge _{i,j} \neg \square \forall x \alpha _i(x) \simeq \alpha _j(x)$
and
$w,\sigma \Vdash \bigwedge _{i,j} \neg \square \forall x \alpha _i(x) \simeq \alpha _j(x)$
and
![]() $ w,\sigma \Vdash \bigwedge _i \mathrm {is} \alpha _i=n_i$
. Now letting
$ w,\sigma \Vdash \bigwedge _i \mathrm {is} \alpha _i=n_i$
. Now letting
![]() $m_1,\dots ,m_k$
be arbitrary, we want to show that there is some
$m_1,\dots ,m_k$
be arbitrary, we want to show that there is some
![]() $u\sqsupseteq w$
such that
$u\sqsupseteq w$
such that
![]() $u,\sigma \Vdash \bigwedge _i \mathrm {is} \alpha _i=n_i^\frown m_i$
. But it is easy to see that there will exist a
$u,\sigma \Vdash \bigwedge _i \mathrm {is} \alpha _i=n_i^\frown m_i$
. But it is easy to see that there will exist a
![]() $u\in \mathbb {P}$
such that
$u\in \mathbb {P}$
such that
![]() $u(\sigma (\alpha _i))=n_i^\frown m_i$
, and such a u will clearly satisfy
$u(\sigma (\alpha _i))=n_i^\frown m_i$
, and such a u will clearly satisfy
![]() $u,\sigma \Vdash \bigwedge _i \mathrm {is} \alpha _i=n_i^\frown m_i$
.
$u,\sigma \Vdash \bigwedge _i \mathrm {is} \alpha _i=n_i^\frown m_i$
.
Theorem 9.7, recall, asserts that every theorem of
![]() $MC_{LS}(Z)$
is forced at every
$MC_{LS}(Z)$
is forced at every
![]() $w\in \mathbb {P}$
. The proof of this theorem uses the following fact.
$w\in \mathbb {P}$
. The proof of this theorem uses the following fact.
Lemma C.1. For all
![]() $w,\sigma _1,\sigma _2$
and for any formula
$w,\sigma _1,\sigma _2$
and for any formula
![]() $A(\alpha _1,\dots ,\alpha _k)$
whose free (i.e., unbound) choice sequence variables are among those shown, if
$A(\alpha _1,\dots ,\alpha _k)$
whose free (i.e., unbound) choice sequence variables are among those shown, if
![]() $\sigma _1(\alpha _i) = \sigma _2(\alpha _i)$
for
$\sigma _1(\alpha _i) = \sigma _2(\alpha _i)$
for
![]() $1\leq i\leq k$
, then
$1\leq i\leq k$
, then
![]() $w,\sigma _1 \Vdash A$
iff
$w,\sigma _1 \Vdash A$
iff
![]() $w,\sigma _2 \Vdash A$
.
$w,\sigma _2 \Vdash A$
.
This lemma can be proved by a straightforward induction on complexity.
Proof of Theorem 9.7
Argue by induction on the length of proof. Since we have seen that the axioms of
![]() $MC_{LS}$
are forced everywhere, we need to show that the axioms of
$MC_{LS}$
are forced everywhere, we need to show that the axioms of
![]() $\mathbf {S4}_{\mathcal {I}}$
are forced everywhere and that the inference rules of
$\mathbf {S4}_{\mathcal {I}}$
are forced everywhere and that the inference rules of
![]() $\mathbf {S4}_{\mathcal {I}}$
preserve the property of being forced everywhere. It is routine to check that each of the axioms of
$\mathbf {S4}_{\mathcal {I}}$
preserve the property of being forced everywhere. It is routine to check that each of the axioms of
![]() $\mathbf {S4}$
—the axioms not involving
$\mathbf {S4}$
—the axioms not involving
![]() $\mathcal {I}$
—are all forced at every
$\mathcal {I}$
—are all forced at every
![]() $w\in \mathbb {P}$
. I will consider a few examples.
$w\in \mathbb {P}$
. I will consider a few examples.
M0.5: Consider the case where o is a choice sequence variable:
![]() $A\leftrightarrow \forall \alpha A$
, where
$A\leftrightarrow \forall \alpha A$
, where
![]() $\alpha $
does not occur free in A. Then by Lemma C.1, for each i we have that
$\alpha $
does not occur free in A. Then by Lemma C.1, for each i we have that
![]() $w,\sigma \Vdash A$
iff
$w,\sigma \Vdash A$
iff
![]() $w,\sigma [\alpha \mapsto i] \Vdash A$
. Hence
$w,\sigma [\alpha \mapsto i] \Vdash A$
. Hence
![]() $w,\sigma \Vdash A $
iff
$w,\sigma \Vdash A $
iff
![]() $w,\sigma \Vdash \forall \alpha A$
.
$w,\sigma \Vdash \forall \alpha A$
.
M0.7: Suppose
![]() $w,\sigma \Vdash t_1=t_1 \wedge t_2 =t_2 \wedge t_1 \neq t_2$
. We want to show that for all
$w,\sigma \Vdash t_1=t_1 \wedge t_2 =t_2 \wedge t_1 \neq t_2$
. We want to show that for all
![]() $u\sqsupseteq w$
,
$u\sqsupseteq w$
,
![]() $u,\sigma \Vdash t_1\neq t_2$
. This can be rigorously proved by induction on the complexity of
$u,\sigma \Vdash t_1\neq t_2$
. This can be rigorously proved by induction on the complexity of
![]() $t_1$
and
$t_1$
and
![]() $t_2$
, but the following sketch summarizes the key ideas. If
$t_2$
, but the following sketch summarizes the key ideas. If
![]() $w,\sigma \Vdash t_1=t_1 \wedge t_2 =t_2$
, then the values of
$w,\sigma \Vdash t_1=t_1 \wedge t_2 =t_2$
, then the values of
![]() $w \circ \sigma $
suffice to fix the denotations of all subterms occurring in
$w \circ \sigma $
suffice to fix the denotations of all subterms occurring in
![]() $t_1$
and
$t_1$
and
![]() $t_2$
. In other words, if
$t_2$
. In other words, if
![]() $\alpha (t)$
occurs anywhere in
$\alpha (t)$
occurs anywhere in
![]() $t_1$
or
$t_1$
or
![]() $t_2$
, then
$t_2$
, then
![]() $t< lh(w(\sigma (\alpha )))$
. Then also for arbitrary
$t< lh(w(\sigma (\alpha )))$
. Then also for arbitrary
![]() $u\sqsupseteq w$
we know that
$u\sqsupseteq w$
we know that
![]() $t< lh(u(\sigma (\alpha )))$
and indeed
$t< lh(u(\sigma (\alpha )))$
and indeed
![]() $(w(\sigma (\alpha )))_t = (u(\sigma (\alpha )))_t$
. So the values of
$(w(\sigma (\alpha )))_t = (u(\sigma (\alpha )))_t$
. So the values of
![]() $t_1$
and
$t_1$
and
![]() $t_2$
are the same at u as they were at w; hence it remains true at u that
$t_2$
are the same at u as they were at w; hence it remains true at u that
![]() $t_1\neq t_2$
.
$t_1\neq t_2$
.
M0.9: If t has no occurrence of choice sequence variables, then
![]() $t=t$
will be forced at every
$t=t$
will be forced at every
![]() $w\in \mathbb {P}$
. On the other hand, by definition we know that
$w\in \mathbb {P}$
. On the other hand, by definition we know that
![]() $\mathcal{R}(Pt,\vec {\alpha },w(\sigma (\alpha )))$
is only true if every term occurring within it denotes, and hence we know that
$\mathcal{R}(Pt,\vec {\alpha },w(\sigma (\alpha )))$
is only true if every term occurring within it denotes, and hence we know that
![]() $w,\sigma \Vdash t=t$
.
$w,\sigma \Vdash t=t$
.
It is also routine to check that the inference rules of S4 preserve the property of being forced everywhere. For instance, consider M0.13: If universal generalization is the last line of a proof, then by i.h. we know that
![]() $w,\sigma \Vdash A$
for every
$w,\sigma \Vdash A$
for every
![]() $w$
and
$w$
and
![]() $\sigma $
. If o is an individual or classical function variable, then we can infer
$\sigma $
. If o is an individual or classical function variable, then we can infer
![]() $\forall o (w,\sigma \Vdash A)$
in our background logic and hence
$\forall o (w,\sigma \Vdash A)$
in our background logic and hence
![]() $w,\sigma \Vdash \forall o A$
. If o is a choice sequence variable, then since
$w,\sigma \Vdash \forall o A$
. If o is a choice sequence variable, then since
![]() $w,\sigma \Vdash A$
for every
$w,\sigma \Vdash A$
for every
![]() $\sigma $
, it follows that for every i,
$\sigma $
, it follows that for every i,
![]() $w,\sigma [\alpha \mapsto i] \Vdash A$
. Hence,
$w,\sigma [\alpha \mapsto i] \Vdash A$
. Hence,
![]() $w,\sigma \Vdash \forall \alpha A$
.
$w,\sigma \Vdash \forall \alpha A$
.
It remains to check that the axioms M1–M7 governing
![]() $\mathcal {I}$
are forced everywhere. M1 and M3 are straightforward, and I will consider M2 and M4–M7.
$\mathcal {I}$
are forced everywhere. M1 and M3 are straightforward, and I will consider M2 and M4–M7.
M2: Suppose
![]() $w,\sigma \Vdash A$
. We want to show
$w,\sigma \Vdash A$
. We want to show
![]() $w,\sigma \Vdash \mathcal {I}A$
. Note that for arbitrary I and
$w,\sigma \Vdash \mathcal {I}A$
. Note that for arbitrary I and
![]() $f_i$
and an arbitrary
$f_i$
and an arbitrary
![]() $[f_i]_I$
-chain C above
$[f_i]_I$
-chain C above
![]() $w$
, we have
$w$
, we have
![]() $w\in C$
. So there is some
$w\in C$
. So there is some
![]() $u\in C$
such that
$u\in C$
such that
![]() $u,\sigma \Vdash A$
; that is,
$u,\sigma \Vdash A$
; that is,
![]() $w,\sigma \Vdash \mathcal {I}A$
.
$w,\sigma \Vdash \mathcal {I}A$
.
M4: Suppose that
![]() $w,\sigma \nVdash \mathcal {I}A$
. Then there are some I and
$w,\sigma \nVdash \mathcal {I}A$
. Then there are some I and
![]() $f_i\in w(i)$
and some
$f_i\in w(i)$
and some
![]() $[f_i]_I$
-chain C above
$[f_i]_I$
-chain C above
![]() $w$
such that for all
$w$
such that for all
![]() $u\in C$
,
$u\in C$
,
![]() $u,\sigma \nVdash A$
. Note that the restriction
$u,\sigma \nVdash A$
. Note that the restriction
![]() $C_u:= C\upharpoonright \lbrace v : v\sqsupseteq u\rbrace $
will be an
$C_u:= C\upharpoonright \lbrace v : v\sqsupseteq u\rbrace $
will be an
![]() $[f_i]_I$
-chain above u. Thus for each
$[f_i]_I$
-chain above u. Thus for each
![]() $u\in C$
,
$u\in C$
,
![]() $C_u$
is an
$C_u$
is an
![]() $[f_i]_I$
-chain above u such that for all
$[f_i]_I$
-chain above u such that for all
![]() $v\in C_u$
,
$v\in C_u$
,
![]() $v,\sigma \nVdash A$
. Thus
$v,\sigma \nVdash A$
. Thus
![]() $u,\sigma \nVdash \mathcal {I}A$
. Since this holds for every
$u,\sigma \nVdash \mathcal {I}A$
. Since this holds for every
![]() $u\in C$
, it follows that
$u\in C$
, it follows that
![]() $w,\sigma \nVdash \mathcal {I}\mathcal {I}A$
.
$w,\sigma \nVdash \mathcal {I}\mathcal {I}A$
.
M5: Suppose
![]() $w,\sigma \nVdash \square \mathcal {I}A$
, so there is some
$w,\sigma \nVdash \square \mathcal {I}A$
, so there is some
![]() $u\sqsupseteq w$
such that
$u\sqsupseteq w$
such that
![]() $u,\sigma \nVdash \mathcal {I}A$
. Then there are some I and
$u,\sigma \nVdash \mathcal {I}A$
. Then there are some I and
![]() $f_i\in u(i)$
and some
$f_i\in u(i)$
and some
![]() $[f_i]_I$
-chain C above u such that for all
$[f_i]_I$
-chain C above u such that for all
![]() $v\in C$
,
$v\in C$
,
![]() $v,\sigma \nVdash A$
. Since
$v,\sigma \nVdash A$
. Since
![]() $f_i\in u(i)$
and
$f_i\in u(i)$
and
![]() $w\sqsubseteq u$
,
$w\sqsubseteq u$
,
![]() $f_i\in w(i)$
as well. If
$f_i\in w(i)$
as well. If
![]() $C'$
is any linear ordering of worlds between
$C'$
is any linear ordering of worlds between
![]() $w$
and u, let
$w$
and u, let
![]() $C_w:=C\cup C'$
. Then
$C_w:=C\cup C'$
. Then
![]() $C_w$
will be an
$C_w$
will be an
![]() $[f_i]_I$
-chain C above
$[f_i]_I$
-chain C above
![]() $w$
. Then for every
$w$
. Then for every
![]() $v\in C_w$
, there is some
$v\in C_w$
, there is some
![]() $v'\sqsupseteq v$
such that
$v'\sqsupseteq v$
such that
![]() $v',\sigma \nVdash A$
. So
$v',\sigma \nVdash A$
. So
![]() $w,\sigma \nVdash \mathcal {I}\square A$
.
$w,\sigma \nVdash \mathcal {I}\square A$
.
M6: I will consider the case where o is a choice sequence variable. The cases of a natural number or classical function variable are substantively similar. Suppose that
![]() $w,\sigma \Vdash \mathcal {I}\forall \alpha A$
. Then for every I and
$w,\sigma \Vdash \mathcal {I}\forall \alpha A$
. Then for every I and
![]() $f_i\in w(i)$
and every
$f_i\in w(i)$
and every
![]() $[f_i]_I$
-chain C above
$[f_i]_I$
-chain C above
![]() $w$
there is some
$w$
there is some
![]() $u\in C$
such that for every j,
$u\in C$
such that for every j,
![]() $u,\sigma [\alpha \mapsto j] \Vdash A$
. By some simple quantifier inferences, this entails that for every j, for every I and
$u,\sigma [\alpha \mapsto j] \Vdash A$
. By some simple quantifier inferences, this entails that for every j, for every I and
![]() $f_i\in w(i)$
and every
$f_i\in w(i)$
and every
![]() $[f_i]_I$
-chain C above
$[f_i]_I$
-chain C above
![]() $w$
there is some
$w$
there is some
![]() $u\in C$
such that
$u\in C$
such that
![]() $u,\sigma [\alpha \mapsto j] \Vdash A$
. That is,
$u,\sigma [\alpha \mapsto j] \Vdash A$
. That is,
![]() $w,\sigma \Vdash \forall \alpha \mathcal {I}A$
.
$w,\sigma \Vdash \forall \alpha \mathcal {I}A$
.
M7 is substantively similar to M6.
Acknowledgments
Thanks are due to Stewart Shapiro, Øystein Linnebo, Neil Tennant, and two anonymous referees for helpful feedback on this paper. In addition, portions of or precursors to this work have been presented at the Ohio State Logic Seminar, the Midwest Philosophy of Math Workshop, and the University of Oslo, and I am grateful for the helpful comments and questions on those occasions.
Funding
This research was supported by the Hong Kong Research Grants Council grant PDFS2021-3H05.