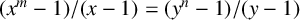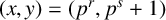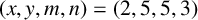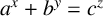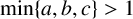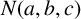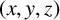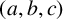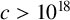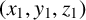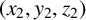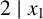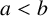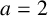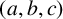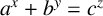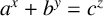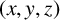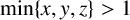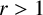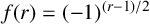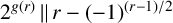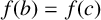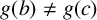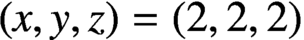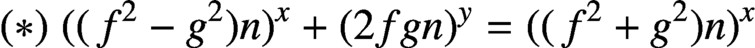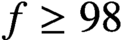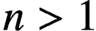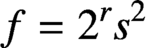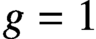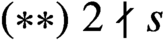10 results
A NOTE ON THE GOORMAGHTIGH EQUATION CONCERNING DIFFERENCE SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 443-452
- Print publication:
- June 2024
-
- Article
- Export citation
ON A CONJECTURE CONCERNING THE NUMBER OF SOLUTIONS TO
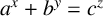 $a^x+b^y=c^z$
$a^x+b^y=c^z$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 40-49
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE NUMBER OF SOLUTIONS OF TERNARY PURELY EXPONENTIAL DIOPHANTINE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 June 2022, pp. 53-65
- Print publication:
- February 2023
-
- Article
- Export citation
A NOTE ON JEŚMANOWICZ’ CONJECTURE CONCERNING NONPRIMITIVE PYTHAGOREAN TRIPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 29-39
- Print publication:
- August 2021
-
- Article
- Export citation
ON THE EXPONENTIAL DIOPHANTINE EQUATION x2+p2m=2yn
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 21 February 2012, pp. 303-314
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
An exponential diophantine equation
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 64 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 17 April 2009, pp. 99-105
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
ON STORER DIFFERENCE SETS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 32 / Issue 6 / November 2000
- Published online by Cambridge University Press:
- 21 December 2000, pp. 663-667
- Print publication:
- November 2000
-
- Article
- Export citation
A note on Jeśmanowicz' conjecture concerning Pythagorean triples
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 59 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 17 April 2009, pp. 477-480
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
A note on the diophantine equation x2 + 7 = yn
-
- Journal:
- Glasgow Mathematical Journal / Volume 39 / Issue 1 / January 1997
- Published online by Cambridge University Press:
- 18 May 2009, pp. 59-63
- Print publication:
- January 1997
-
- Article
-
- You have access
- Export citation
A note on the diophantine equation (xm − l) / (x − 1) = yn + l
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 116 / Issue 3 / November 1994
- Published online by Cambridge University Press:
- 24 October 2008, pp. 385-389
- Print publication:
- November 1994
-
- Article
- Export citation