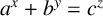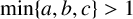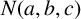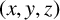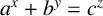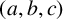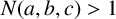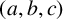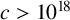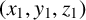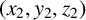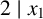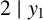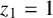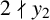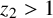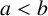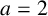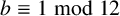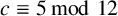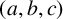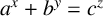1 Introduction
Let
![]() $\mathbb {N} $
be the set of all positive integers. Let a, b, c be fixed coprime positive integers with
$\mathbb {N} $
be the set of all positive integers. Let a, b, c be fixed coprime positive integers with
![]() $\min \{ a,b,c\}>1$
. The equation
$\min \{ a,b,c\}>1$
. The equation
has been studied deeply with abundant results (see [Reference Le, Scott and Styer14], see also [Reference Bennett2]). In 1933, Mahler [Reference Mahler15] used his p-adic analogue of the Diophantine approximation method of Thue–Siegel to prove that (1.1) has only finitely many solutions
![]() $(x,y,z)$
. However, his method is ineffective. Let
$(x,y,z)$
. However, his method is ineffective. Let
![]() $N(a,b,c)$
denote the number of solutions
$N(a,b,c)$
denote the number of solutions
![]() $(x,y,z)$
of (1.1). An effective upper bound for
$(x,y,z)$
of (1.1). An effective upper bound for
![]() $N(a,b,c)$
was first given by Gel’fond [Reference Gel’fond8]. A straightforward application of an upper bound on the number of solutions of binary S-unit equations due to Beukers and Schlickewei [Reference Beukers and Schlickewei5] gives
$N(a,b,c)$
was first given by Gel’fond [Reference Gel’fond8]. A straightforward application of an upper bound on the number of solutions of binary S-unit equations due to Beukers and Schlickewei [Reference Beukers and Schlickewei5] gives
![]() $N(a,b,c) \le 2^{36}$
. The following more accurate upper bounds for
$N(a,b,c) \le 2^{36}$
. The following more accurate upper bounds for
![]() $N(a,b,c)$
have been obtained in recent years.
$N(a,b,c)$
have been obtained in recent years.
-
(i) (Scott and Styer [Reference Scott and Styer22]) If
 $ 2 \nmid c$
, then
$ 2 \nmid c$
, then
 $N(a,b,c) \le 2$
.
$N(a,b,c) \le 2$
. -
(ii) (Hu and Le [Reference Hu and Le9]) If
 $\max \{ a,b,c\}> 5 \cdot 10^{27}$
, then
$\max \{ a,b,c\}> 5 \cdot 10^{27}$
, then
 $N(a,b,c) \le 3$
.
$N(a,b,c) \le 3$
. -
(iii) (Hu and Le [Reference Hu and Le10]) If
 $2 \mid c$
and
$2 \mid c$
and
 $\max \{ a,b,c\}> 10^{62}$
, then
$\max \{ a,b,c\}> 10^{62}$
, then
 $N(a,b,c) \le 2$
.
$N(a,b,c) \le 2$
. -
(iv) (Miyazaki and Pink [Reference Miyazaki and Pink16]) If
 $2 \mid c$
,
$2 \mid c$
,
 $a<b$
and
$a<b$
and
 $\max \{a,b,c \} \le 10^{62}$
, then
$\max \{a,b,c \} \le 10^{62}$
, then
 $N(a,b,c) \le 2$
except for
$N(a,b,c) \le 2$
except for
 $N(3,5,2) = 3$
.
$N(3,5,2) = 3$
.
Nevertheless, the problem of establishing
![]() $N(a,b,c) \le 1$
with a finite number of exceptions remains open. This open question is addressed by the following conjecture in [Reference Scott and Styer22]. Assuming without loss of generality that a, b and c are not perfect powers, the conjecture may be formulated as follows.
$N(a,b,c) \le 1$
with a finite number of exceptions remains open. This open question is addressed by the following conjecture in [Reference Scott and Styer22]. Assuming without loss of generality that a, b and c are not perfect powers, the conjecture may be formulated as follows.
Conjecture 1.1. For
![]() $a<b$
, we have
$a<b$
, we have
![]() $N(a,b,c) \le 1$
, except for:
$N(a,b,c) \le 1$
, except for:
-
(i)
 $N(2, 2^r-1, 2^r+1)=2$
,
$N(2, 2^r-1, 2^r+1)=2$
,
 $(x,y,z)=(1,1,1)$
and
$(x,y,z)=(1,1,1)$
and
 $(r+2, 2, 2)$
, where r is a positive integer with
$(r+2, 2, 2)$
, where r is a positive integer with
 $r \ge 2$
;
$r \ge 2$
; -
(ii)
 $N(2, 3, 11)=2$
,
$N(2, 3, 11)=2$
,
 $(x,y,z)=(1,2,1)$
and
$(x,y,z)=(1,2,1)$
and
 $(3,1,1)$
;
$(3,1,1)$
; -
(iii)
 $N(2, 3, 35)=2$
,
$N(2, 3, 35)=2$
,
 $(x,y,z)=(3,3,1)$
and
$(x,y,z)=(3,3,1)$
and
 $(5,1,1)$
;
$(5,1,1)$
; -
(vi)
 $N(2, 3, 259)=2$
,
$N(2, 3, 259)=2$
,
 $(x,y,z)=(4,5,1)$
and
$(x,y,z)=(4,5,1)$
and
 $(8,1,1)$
;
$(8,1,1)$
; -
(v)
 $N(2, 5, 3)=2$
,
$N(2, 5, 3)=2$
,
 $(x,y,z)=(1,2,3)$
and
$(x,y,z)=(1,2,3)$
and
 $(2,1,2)$
;
$(2,1,2)$
; -
(vi)
 $N(2, 5, 133)=2$
,
$N(2, 5, 133)=2$
,
 $(x,y,z)=(3,3,1)$
and
$(x,y,z)=(3,3,1)$
and
 $(7,1,1)$
;
$(7,1,1)$
; -
(vii)
 $N(2, 7, 3)=2$
,
$N(2, 7, 3)=2$
,
 $(x,y,z)=(1,1,2)$
and
$(x,y,z)=(1,1,2)$
and
 $(5,2,4)$
;
$(5,2,4)$
; -
(viii)
 $N(2, 89, 91)=2$
,
$N(2, 89, 91)=2$
,
 $(x,y,z)=(1,1,1)$
and
$(x,y,z)=(1,1,1)$
and
 $(13,1,2)$
;
$(13,1,2)$
; -
(xi)
 $N(2, 91, 8283)=2$
,
$N(2, 91, 8283)=2$
,
 $(x,y,z)=(1,2,1)$
and
$(x,y,z)=(1,2,1)$
and
 $(13,1,1)$
;
$(13,1,1)$
; -
(x)
 $N(3,5,2)=3$
,
$N(3,5,2)=3$
,
 $(x,y,z)=(1,1,3)$
,
$(x,y,z)=(1,1,3)$
,
 $(1,3,7)$
, and
$(1,3,7)$
, and
 $(3,1,5)$
;
$(3,1,5)$
; -
(xi)
 $N(3,10,13)=2$
,
$N(3,10,13)=2$
,
 $(x,y,z)=(1,1,1)$
and
$(x,y,z)=(1,1,1)$
and
 $(7,1,3)$
;
$(7,1,3)$
; -
(xii)
 $N(3,13,2)=2$
,
$N(3,13,2)=2$
,
 $(x,y,z)=(1,1,4)$
and
$(x,y,z)=(1,1,4)$
and
 $(5,1,8)$
;
$(5,1,8)$
; -
(xiii)
 $N(3, 13, 2200)=2$
,
$N(3, 13, 2200)=2$
,
 $(x,y,z)=(1,3,1)$
and
$(x,y,z)=(1,3,1)$
and
 $(7,1,1)$
.
$(7,1,1)$
.
Later in this paper, in referring to the solutions in cases (i) through (xiii) above, it will be helpful to have established the following result.
Lemma 1.2. The values of
![]() $N(a,b,c)$
in Conjecture 1.1 are exact: there are no further solutions in any of the thirteen cases.
$N(a,b,c)$
in Conjecture 1.1 are exact: there are no further solutions in any of the thirteen cases.
Proof. For cases (i) through (xii), this follows from Theorem 1 of [Reference Scott and Styer22] and Theorem 6 of [Reference Scott19]. For case (xiii), consideration modulo 16 shows that
![]() $z>1$
requires
$z>1$
requires
![]() $4 \mid x-y$
, which contradicts consideration modulo 5. So
$4 \mid x-y$
, which contradicts consideration modulo 5. So
![]() $z=1$
, and there are only two solutions.
$z=1$
, and there are only two solutions.
Although the results on (1.1) known so far support Conjecture 1.1, it is generally far from being resolved. This difficult problem is made more approachable by taking c prime. More than thirty years ago, the first author [Reference Le12] discussed the upper bound for
![]() $N(a,b,c)$
when a, b, c are distinct primes. Many authors have used this approach to the problem. Later, [Reference Scott and Styer22] removed the difficulty caused by taking c composite when c is odd, and Hu and Le [Reference Hu and Le10] and Miyazaki and Pink [Reference Miyazaki and Pink16] handled even composite c; these later results established
$N(a,b,c)$
when a, b, c are distinct primes. Many authors have used this approach to the problem. Later, [Reference Scott and Styer22] removed the difficulty caused by taking c composite when c is odd, and Hu and Le [Reference Hu and Le10] and Miyazaki and Pink [Reference Miyazaki and Pink16] handled even composite c; these later results established
![]() $N(a,b,c) \le 2$
with the single exceptional case
$N(a,b,c) \le 2$
with the single exceptional case
![]() $(a,b,c) = (3,5,2)$
.
$(a,b,c) = (3,5,2)$
.
Establishing
![]() $N(a,b,c) \le 1$
involves many exceptional cases and is, in general, much more difficult, suggesting perhaps that the old approach of considering only prime bases may be a practical way to begin considering this problem.
$N(a,b,c) \le 1$
involves many exceptional cases and is, in general, much more difficult, suggesting perhaps that the old approach of considering only prime bases may be a practical way to begin considering this problem.
Our first result requires c prime with congruence restrictions on a and b not necessarily prime.
Theorem 1.3. If
![]() $a \equiv 2 \bmod 3$
,
$a \equiv 2 \bmod 3$
,
![]() $b \not \equiv 0\, \bmod 3$
and
$b \not \equiv 0\, \bmod 3$
and
![]() $c>3$
is an odd prime, then
$c>3$
is an odd prime, then
![]() $N(a,b,c) \le 1$
, except for the following possibility: (1.1) has exactly two solutions
$N(a,b,c) \le 1$
, except for the following possibility: (1.1) has exactly two solutions
![]() $(x_1, y_1, z_1)$
and
$(x_1, y_1, z_1)$
and
![]() $(x_2, y_2, z_2)$
, and these solutions satisfy
$(x_2, y_2, z_2)$
, and these solutions satisfy
![]() $2 \mid x_1$
,
$2 \mid x_1$
,
![]() $2 \mid y_1$
,
$2 \mid y_1$
,
![]() $2 \nmid z_1$
and
$2 \nmid z_1$
and
![]() $2 \nmid y_2$
, with
$2 \nmid y_2$
, with
![]() $c \equiv 5 \bmod 12$
.
$c \equiv 5 \bmod 12$
.
Theorem 1.3 is used to establish the following result.
Theorem 1.4. If a, b, c are distinct primes with
![]() $a<b$
and
$a<b$
and
![]() $N(a,b,c)> 1$
, then
$N(a,b,c)> 1$
, then
![]() $c \equiv 5 \bmod 12$
, and there must be exactly two solutions
$c \equiv 5 \bmod 12$
, and there must be exactly two solutions
![]() $(x_1,y_1,z_1)$
and
$(x_1,y_1,z_1)$
and
![]() $(x_2,y_2,z_2)$
, with
$(x_2,y_2,z_2)$
, with
![]() $2 \mid x_1$
,
$2 \mid x_1$
,
![]() $2 \mid y_1$
,
$2 \mid y_1$
,
![]() $z_1=1$
and
$z_1=1$
and
![]() $2 \nmid y_2$
, except for
$2 \nmid y_2$
, except for
![]() $(a,b,c) = (2,3,5)$
,
$(a,b,c) = (2,3,5)$
,
![]() $(2,3,11)$
,
$(2,3,11)$
,
![]() $(2,5,3)$
,
$(2,5,3)$
,
![]() $(2,7,3)$
,
$(2,7,3)$
,
![]() $(3,5,2)$
and
$(3,5,2)$
and
![]() $(3,13,2)$
.
$(3,13,2)$
.
Further restrictions are given by the following result.
Theorem 1.5. If a, b, c are distinct primes with
![]() $a<b$
and
$a<b$
and
![]() $N(a,b,c)> 1$
, then, if
$N(a,b,c)> 1$
, then, if
![]() $(a,b,c) \ne (2,3,5)$
,
$(a,b,c) \ne (2,3,5)$
,
![]() $(2,3,11)$
,
$(2,3,11)$
,
![]() $(2,5,3)$
,
$(2,5,3)$
,
![]() $(2,7,3)$
,
$(2,7,3)$
,
![]() $(3,5,2)$
or
$(3,5,2)$
or
![]() $(3,13,2)$
, we must have
$(3,13,2)$
, we must have
![]() $a=2$
with
$a=2$
with
![]() $b \equiv 1 \bmod 12$
and
$b \equiv 1 \bmod 12$
and
![]() $c \equiv 5 \bmod 12$
; further, if
$c \equiv 5 \bmod 12$
; further, if
![]() $b \equiv 1 \bmod 24$
, then
$b \equiv 1 \bmod 24$
, then
![]() $c \equiv 17 \bmod 24$
.
$c \equiv 17 \bmod 24$
.
Corollary 1.6. If a, b, c are distinct primes with
![]() $a<b$
and
$a<b$
and
![]() $N(a,b,c)>1$
, then, if
$N(a,b,c)>1$
, then, if
![]() $(a,b,c) \ne (2,3,5)$
,
$(a,b,c) \ne (2,3,5)$
,
![]() $(2,3,11)$
,
$(2,3,11)$
,
![]() $(2,5,3)$
,
$(2,5,3)$
,
![]() $(2,7,3)$
,
$(2,7,3)$
,
![]() $(3,5,2)$
or
$(3,5,2)$
or
![]() $(3,13,2)$
, we must have
$(3,13,2)$
, we must have
![]() $N(a,b,c) = 2$
and, letting the two solutions be
$N(a,b,c) = 2$
and, letting the two solutions be
![]() $(x_1,y_1,z_1)$
and
$(x_1,y_1,z_1)$
and
![]() $(x_2,y_2,z_2)$
as in Theorem 1.4, we must have
$(x_2,y_2,z_2)$
as in Theorem 1.4, we must have
![]() $z_2> 1. $
$z_2> 1. $
In a later section, we will use the following version of Conjecture 1.1 in which a, b and c are restricted to prime values.
Conjecture 1.7. For a, b and c distinct primes with
![]() $a<b$
, we have
$a<b$
, we have
![]() $N(a,b,c) \le 1$
, except for:
$N(a,b,c) \le 1$
, except for:
-
(i)
 $N(2,3,5) = 2$
,
$N(2,3,5) = 2$
,
 $(x,y,z) = (1,1,1)$
and
$(x,y,z) = (1,1,1)$
and
 $(4,2,2)$
;
$(4,2,2)$
; -
(ii)
 $N(2, 3, 11)=2$
,
$N(2, 3, 11)=2$
,
 $(x,y,z)=(1,2,1)$
and
$(x,y,z)=(1,2,1)$
and
 $(3,1,1)$
;
$(3,1,1)$
; -
(iii)
 $N(2, 5, 3)=2$
,
$N(2, 5, 3)=2$
,
 $(x,y,z)=(1,2,3)$
and
$(x,y,z)=(1,2,3)$
and
 $(2,1,2)$
;
$(2,1,2)$
; -
(iv)
 $N(2, 7, 3)=2$
,
$N(2, 7, 3)=2$
,
 $(x,y,z)=(1,1,2)$
and
$(x,y,z)=(1,1,2)$
and
 $(5,2,4)$
;
$(5,2,4)$
; -
(v)
 $N(3,5,2)=3$
,
$N(3,5,2)=3$
,
 $(x,y,z)=(1,1,3)$
,
$(x,y,z)=(1,1,3)$
,
 $(1,3,7)$
and
$(1,3,7)$
and
 $(3,1,5)$
;
$(3,1,5)$
; -
(vi)
 $N(3,13,2)=2$
,
$N(3,13,2)=2$
,
 $(x,y,z)=(1,1,4)$
and
$(x,y,z)=(1,1,4)$
and
 $(5,1,8)$
.
$(5,1,8)$
.
In the final section of this paper, we will explain a method by which we have shown the following result.
Theorem 1.8. Any counterexample to Conjecture 1.7 must have
This result is in marked contrast to results which can be obtained without assuming a, b and c are prime: in that more general case, the lower bound on c when
![]() $(a,b,c)$
gives a counterexample to Conjecture 1.1 is still quite low (the latest such results are given by Miyazaki and Pink [Reference Miyazaki and Pink17] in considering Conjecture 1.1 for the special case in which either a or b is congruent to
$(a,b,c)$
gives a counterexample to Conjecture 1.1 is still quite low (the latest such results are given by Miyazaki and Pink [Reference Miyazaki and Pink17] in considering Conjecture 1.1 for the special case in which either a or b is congruent to
![]() $\pm 1$
modulo c). Theorem 1.8 improves Lemma 2.9 in Section 2 which follows.
$\pm 1$
modulo c). Theorem 1.8 improves Lemma 2.9 in Section 2 which follows.
2 Preliminaries
We now divide all solutions
![]() $(x,y,z)$
of (1.1) into four classes according to the parities of x and y:
$(x,y,z)$
of (1.1) into four classes according to the parities of x and y:
![]() $2\mid x$
and
$2\mid x$
and
![]() $2 \mid y$
;
$2 \mid y$
;
![]() $2 \nmid x$
and
$2 \nmid x$
and
![]() $2 \mid y$
;
$2 \mid y$
;
![]() $2 \mid x$
and
$2 \mid x$
and
![]() $2 \nmid y$
; or
$2 \nmid y$
; or
![]() $2 \nmid x$
and
$2 \nmid x$
and
![]() $2 \nmid y$
. We will call these classes the parity classes of (1.1).
$2 \nmid y$
. We will call these classes the parity classes of (1.1).
Lemma 2.1. If c is an odd prime, then, for a given parity class, there is at most one solution
![]() $(x,y,z)$
to (1.1), except for
$(x,y,z)$
to (1.1), except for
![]() $(a,b,c)=(3,10,13)$
or
$(a,b,c)=(3,10,13)$
or
![]() $(10,3,13)$
.
$(10,3,13)$
.
Proof. Since c is an odd prime, using the notation of [Reference Scott and Styer22], we see that for any given parity class of (1.1), there is only one ideal factorisation in
![]() $C_D$
. Therefore, by Lemma 2 of [Reference Scott and Styer22], we obtain the lemma immediately.
$C_D$
. Therefore, by Lemma 2 of [Reference Scott and Styer22], we obtain the lemma immediately.
Lemma 2.2 [Reference Scott and Styer20, Lemma 2].
The equation
has no solutions in positive integers
![]() $(x,y,z,n)$
with
$(x,y,z,n)$
with
![]() $z>1$
except for
$z>1$
except for
![]() $3^2+2^4 = 5^2$
.
$3^2+2^4 = 5^2$
.
Lemma 2.3. Let X, n be positive integers with
![]() $2 \nmid X$
and
$2 \nmid X$
and
![]() $n>1$
. Then
$n>1$
. Then
![]() $|X^2 - 2^n|> 2^{0.26 n}$
, except for
$|X^2 - 2^n|> 2^{0.26 n}$
, except for
![]() $X^2 - 2^n = 1$
or
$X^2 - 2^n = 1$
or
![]() $-7$
.
$-7$
.
Proof. This lemma is a special case of Corollary 1.7 of [Reference Bauer and Bennett1] with
![]() $y=2$
.
$y=2$
.
Lemma 2.4 [Reference Cohn7, Reference Le13].
The equation
has only the solutions
![]() $(X,Y,m,n) = (5,3,1,3)$
,
$(X,Y,m,n) = (5,3,1,3)$
,
![]() $(11,5,2,3)$
and
$(11,5,2,3)$
and
![]() $(7,3,5,4)$
.
$(7,3,5,4)$
.
Lemma 2.5 [Reference Bennett and Skinner4, Theorem 8.4].
The equation
has only the solution
![]() $(X,Y,m,n) = (71, 17, 7, 3)$
.
$(X,Y,m,n) = (71, 17, 7, 3)$
.
Lemma 2.6 [Reference Scott and Styer20, Theorem 6].
Let A, B be distinct odd positive primes. For a given positive integer k, the equation
has at most one solution in positive integers
![]() $(m,n)$
.
$(m,n)$
.
Lemma 2.7 [Reference Scott19, Theorem 6].
If
![]() $a<b$
and
$a<b$
and
![]() $c=2$
, then
$c=2$
, then
![]() $N(a,b,2) \le 1$
, except for
$N(a,b,2) \le 1$
, except for
![]() $N(3,5,2)=3$
and
$N(3,5,2)=3$
and
![]() $N(3,13,2)=2$
.
$N(3,13,2)=2$
.
Lemma 2.8 [Reference Scott and Styer22].
If
![]() $2 \nmid c$
, then
$2 \nmid c$
, then
![]() $N(a,b,c) \le 2$
.
$N(a,b,c) \le 2$
.
Lemma 2.9 [Reference Cao6].
If a, b, c are distinct primes with
![]() $\max \{ a,b,c\} < 100$
, then Conjecture 1.7 is true.
$\max \{ a,b,c\} < 100$
, then Conjecture 1.7 is true.
Lemma 2.10 [Reference Scott and Styer21, Lemma 4.2].
The equation
has no solutions with integer
![]() $r>1$
when D is a positive integer congruent to 2 mod 4 and m is any integer, except for
$r>1$
when D is a positive integer congruent to 2 mod 4 and m is any integer, except for
![]() $D=2$
,
$D=2$
,
![]() $r=3$
.
$r=3$
.
Further, when
![]() $D \equiv 0 \bmod 4$
is a positive integer such that
$D \equiv 0 \bmod 4$
is a positive integer such that
![]() $1+D$
is prime or a prime power, (2.5) has no solutions with integer
$1+D$
is prime or a prime power, (2.5) has no solutions with integer
![]() $r>1$
except for
$r>1$
except for
![]() $D=4$
,
$D=4$
,
![]() $r=3$
.
$r=3$
.
Lemma 2.11. If the equation
has a solution in positive integers
![]() $(m,n,x,y)$
with
$(m,n,x,y)$
with
![]() $m \ne x$
, then
$m \ne x$
, then
![]() $d=1$
,
$d=1$
,
![]() $-5$
or
$-5$
or
![]() $-13$
.
$-13$
.
Proof. This follows easily from a conjecture of Pillai [Reference Pillai18] first proven by Stroeker and Tijdeman [Reference Stroeker, Tijdeman, Lenstra and Tijdeman23] using lower bonds on linear forms in logarithms. It is also an immediate consequence of the elementary corollary to Theorem 4 of [Reference Scott19].
Lemma 2.12. If
![]() $N(a,b,c)>1$
when
$N(a,b,c)>1$
when
![]() $a \equiv 2 \bmod 3$
,
$a \equiv 2 \bmod 3$
,
![]() $b \not \equiv 0\, \mod 3$
and c is an odd prime, then (1.1) has exactly two solutions
$b \not \equiv 0\, \mod 3$
and c is an odd prime, then (1.1) has exactly two solutions
![]() $(x_1, y_1, z_1)$
and
$(x_1, y_1, z_1)$
and
![]() $(x_2,y_2,z_2)$
, where
$(x_2,y_2,z_2)$
, where
![]() $2 \nmid y_1 - y_2$
.
$2 \nmid y_1 - y_2$
.
Proof. If
![]() $a \equiv 2 \bmod 3$
,
$a \equiv 2 \bmod 3$
,
![]() $b \not \equiv 0 \bmod 3$
and c is an odd prime, then the parity of y determines the parity class. Since Lemma 2.1 shows that there is at most one solution per parity class, we see that
$b \not \equiv 0 \bmod 3$
and c is an odd prime, then the parity of y determines the parity class. Since Lemma 2.1 shows that there is at most one solution per parity class, we see that
![]() $N(a,b,c)>1$
implies that there are exactly two solutions
$N(a,b,c)>1$
implies that there are exactly two solutions
![]() $(x_1, y_1, z_1)$
and
$(x_1, y_1, z_1)$
and
![]() $(x_2,y_2,z_2)$
and
$(x_2,y_2,z_2)$
and
![]() $ 2 \nmid y_1 - y_2$
.
$ 2 \nmid y_1 - y_2$
.
Lemma 2.13 [Reference Bennett3, Theorem 1.1].
Let c and b be positive integers. Then there exists at most one pair of positive integers
![]() $(z,y)$
for which
$(z,y)$
for which
3 Proofs of Theorems 1.3 and 1.4
Proof of Theorem 1.3.
Assume
![]() $N(a,b,c)>1$
with
$N(a,b,c)>1$
with
![]() $a \equiv 2 \bmod 3$
,
$a \equiv 2 \bmod 3$
,
![]() $b \not \equiv 0\, \mod 3$
and
$b \not \equiv 0\, \mod 3$
and
![]() $c>3$
an odd prime. By Lemma 2.12, there must be exactly two solutions
$c>3$
an odd prime. By Lemma 2.12, there must be exactly two solutions
![]() $(x_1, y_1, z_1)$
and
$(x_1, y_1, z_1)$
and
![]() $(x_2,y_2,z_2)$
, with
$(x_2,y_2,z_2)$
, with
![]() $2 \nmid y_1 - y_2$
. Take
$2 \nmid y_1 - y_2$
. Take
![]() $y_1$
even. Then, since
$y_1$
even. Then, since
![]() $c>3$
, consideration modulo 3 shows that
$c>3$
, consideration modulo 3 shows that
![]() $2 \mid x_1$
,
$2 \mid x_1$
,
![]() $2 \mid y_1$
and
$2 \mid y_1$
and
![]() $2 \nmid z_1$
, which requires
$2 \nmid z_1$
, which requires
![]() $c \equiv 2 \bmod 3$
and
$c \equiv 2 \bmod 3$
and
![]() $c \equiv 1 \bmod 4$
. Thus,
$c \equiv 1 \bmod 4$
. Thus,
![]() $c \equiv 5 \bmod 12$
.
$c \equiv 5 \bmod 12$
.
Proof of Theorem 1.4.
Assume that a, b and c are distinct primes with
![]() $a<b$
. If
$a<b$
. If
![]() $N(a,b,c)>1$
, we can take
$N(a,b,c)>1$
, we can take
![]() $a=2$
(
$a=2$
(
![]() $c \ne 2$
by Lemma 2.7, except for
$c \ne 2$
by Lemma 2.7, except for
![]() $(a,b,c)=(3,5,2)$
and
$(a,b,c)=(3,5,2)$
and
![]() $(3,13,2)$
, given as exceptions in the statement of the theorem).
$(3,13,2)$
, given as exceptions in the statement of the theorem).
Additionally, we can also take
![]() $b \ne 3$
: using Lemma 2.2, we find that if the equation
$b \ne 3$
: using Lemma 2.2, we find that if the equation
![]() $2^x+3^y=c^z$
has two solutions
$2^x+3^y=c^z$
has two solutions
![]() $(x_1,y_1,z_1)$
and
$(x_1,y_1,z_1)$
and
![]() $(x_2,y_2,z_2)$
, we either must have
$(x_2,y_2,z_2)$
, we either must have
![]() $c=5$
with
$c=5$
with
![]() $\{z_1,z_2 \}=\{ 1,2 \}$
or we must have
$\{z_1,z_2 \}=\{ 1,2 \}$
or we must have
![]() $z_1=z_2=1$
, in which case we have
$z_1=z_2=1$
, in which case we have
![]() $3^{y_1}-2^{x_2} = 3^{y_2}-2^{x_1} = d$
, where
$3^{y_1}-2^{x_2} = 3^{y_2}-2^{x_1} = d$
, where
![]() $d=1$
,
$d=1$
,
![]() $-5$
or
$-5$
or
![]() $-13$
by Lemma 2.11; recalling Lemma 1.2 and using the solutions given in cases (x) and (iii) in Conjecture 1.1, we see that
$-13$
by Lemma 2.11; recalling Lemma 1.2 and using the solutions given in cases (x) and (iii) in Conjecture 1.1, we see that
![]() $d = -5$
corresponds to
$d = -5$
corresponds to
![]() $c=35$
, while using case (xii) with case (iv) shows that
$c=35$
, while using case (xii) with case (iv) shows that
![]() $d=-13$
corresponds to
$d=-13$
corresponds to
![]() $c=259$
; since neither of these values of c is prime, we must have
$c=259$
; since neither of these values of c is prime, we must have
![]() $d=1$
, and it is a familiar elementary result that we must have
$d=1$
, and it is a familiar elementary result that we must have
![]() $(x_1, y_1, x_2, y_2) = (1,2,3,1)$
giving
$(x_1, y_1, x_2, y_2) = (1,2,3,1)$
giving
![]() $c=11$
.
$c=11$
.
Thus we find that the only cases with
![]() $a=2$
,
$a=2$
,
![]() $b=3$
and
$b=3$
and
![]() $N(a,b,c)>1$
are
$N(a,b,c)>1$
are
![]() $(a,b,c) = (2,3,5)$
and
$(a,b,c) = (2,3,5)$
and
![]() $(2,3,11)$
, given as exceptions in the statement of the theorem.
$(2,3,11)$
, given as exceptions in the statement of the theorem.
Now assume
![]() $a=2$
and
$a=2$
and
![]() $c=3$
, and assume (1.1) has two solutions
$c=3$
, and assume (1.1) has two solutions
![]() $(x_1,y_1,z_1)$
and
$(x_1,y_1,z_1)$
and
![]() $(x_2,y_2,z_2)$
. By Lemma 2.12, we can assume
$(x_2,y_2,z_2)$
. By Lemma 2.12, we can assume
![]() $2 \mid y_1$
. If
$2 \mid y_1$
. If
![]() $z_1$
is even, then
$z_1$
is even, then
![]() $3^{z_1/2} - b^{y_1/2} =~2$
and
$3^{z_1/2} - b^{y_1/2} =~2$
and
![]() $3^{z_1/2}+b^{y_1/2} = 2^{x_1-1}$
, so that
$3^{z_1/2}+b^{y_1/2} = 2^{x_1-1}$
, so that
![]() $ 3^{z_1/2} = 2^{x_1 -2} +1$
; it is a familiar elementary result that we must have either
$ 3^{z_1/2} = 2^{x_1 -2} +1$
; it is a familiar elementary result that we must have either
![]() $(x_1, z_1) = (3,2)$
(giving
$(x_1, z_1) = (3,2)$
(giving
![]() $b^{y_1/2} = 1$
) or
$b^{y_1/2} = 1$
) or
![]() $(x_1, z_1) = (5,4)$
(giving
$(x_1, z_1) = (5,4)$
(giving
![]() $b^{y_1/2} = 7$
). Since
$b^{y_1/2} = 7$
). Since
![]() $b>1$
, we find that
$b>1$
, we find that
![]() $(a,b,c) = (2,7,3)$
is the only possibility when
$(a,b,c) = (2,7,3)$
is the only possibility when
![]() $z_1$
is even.
$z_1$
is even.
Additionally, if
![]() $2 \nmid z_1$
when
$2 \nmid z_1$
when
![]() $a=2$
and
$a=2$
and
![]() $c=3$
, then, since
$c=3$
, then, since
![]() $2 \mid y_1$
, we have
$2 \mid y_1$
, we have
![]() $x_1 = 1$
, and we can factor in
$x_1 = 1$
, and we can factor in
![]() $\mathbb {Q} (\sqrt {-2})$
:
$\mathbb {Q} (\sqrt {-2})$
:
where the ‘
![]() $\pm $
’ are independent. Since clearly
$\pm $
’ are independent. Since clearly
![]() $z_1>1$
, we can use Lemma 2.10 to see that
$z_1>1$
, we can use Lemma 2.10 to see that
![]() $z_1 =3$
and
$z_1 =3$
and
![]() $(a,b,c)=(2,5,3)$
.
$(a,b,c)=(2,5,3)$
.
Thus, recalling Lemma 1.2, we find that the only cases with
![]() $a=2$
,
$a=2$
,
![]() $c=3$
and
$c=3$
and
![]() $N(a,b,c)>1$
are
$N(a,b,c)>1$
are
![]() $(a,b,c)=(2,7,3)$
and
$(a,b,c)=(2,7,3)$
and
![]() $(2,5,3)$
, given as exceptions in the statement of the theorem.
$(2,5,3)$
, given as exceptions in the statement of the theorem.
So, excluding the six exceptions given in the statement of the theorem, we can assume
![]() $a=2$
,
$a=2$
,
![]() $b \ne 3$
and
$b \ne 3$
and
![]() $c \ne 3$
when
$c \ne 3$
when
![]() $N(a,b,c)>1$
for a triple of primes
$N(a,b,c)>1$
for a triple of primes
![]() $(a,b,c)$
. Now, Theorem 1.4 follows immediately from Theorem 1.3, except for the conclusion
$(a,b,c)$
. Now, Theorem 1.4 follows immediately from Theorem 1.3, except for the conclusion
![]() $z_1=1$
. To see that
$z_1=1$
. To see that
![]() $z_1=1$
, note that, since
$z_1=1$
, note that, since
![]() $2 \nmid z_1$
, it suffices to use Lemma 2.4, noting
$2 \nmid z_1$
, it suffices to use Lemma 2.4, noting
![]() $(a,b,c) = (2,5,3)$
and
$(a,b,c) = (2,5,3)$
and
![]() $(2,7,3)$
have been excepted, and handling
$(2,7,3)$
have been excepted, and handling
![]() $(2,11,5)$
using Lemma 2.1 with consideration modulo 3 and modulo 5.
$(2,11,5)$
using Lemma 2.1 with consideration modulo 3 and modulo 5.
4 Proofs of Theorem 1.5 and Corollary 1.6
Proof of Theorem 1.5.
Assume a, b and c are distinct primes with
![]() $a<b$
,
$a<b$
,
![]() $(a,b,c) \ne (2,3,5)$
,
$(a,b,c) \ne (2,3,5)$
,
![]() $(2,3,11)$
,
$(2,3,11)$
,
![]() $(2,5,3)$
,
$(2,5,3)$
,
![]() $(2,7,3)$
,
$(2,7,3)$
,
![]() $(3,5,2)$
or
$(3,5,2)$
or
![]() $(3,13,2)$
, and
$(3,13,2)$
, and
![]() $N(a,b,c)> 1$
. From Theorem 1.4,
$N(a,b,c)> 1$
. From Theorem 1.4,
and
Assume first
We have
Since
![]() $2 \mid x_2$
and
$2 \mid x_2$
and
![]() $2 \nmid y_2$
, by (4.1) and (4.4), we get
$2 \nmid y_2$
, by (4.1) and (4.4), we get
![]() $ b \equiv b^{y_2} \equiv c^{z_2} - 2^{x_2} \equiv 1-0 \equiv 1 \bmod 4$
. Hence, by (4.3),
$ b \equiv b^{y_2} \equiv c^{z_2} - 2^{x_2} \equiv 1-0 \equiv 1 \bmod 4$
. Hence, by (4.3),
If
![]() $c \equiv 5 \bmod 8$
and
$c \equiv 5 \bmod 8$
and
![]() $b \equiv 1 \bmod 8$
, then from (4.2) and (4.4), we get
$b \equiv 1 \bmod 8$
, then from (4.2) and (4.4), we get
![]() $x_1=2$
and
$x_1=2$
and
![]() $x_2=2$
, respectively. This implies that (2.2) has two solutions
$x_2=2$
, respectively. This implies that (2.2) has two solutions
![]() $(m,n)= (1, y_1)$
and
$(m,n)= (1, y_1)$
and
![]() $(z_2, y_2)$
for
$(z_2, y_2)$
for
![]() $(A,B) = (c,b)$
and
$(A,B) = (c,b)$
and
![]() $k=2$
. By Lemma 2.6, this is impossible. Hence, by (4.1) and (4.5),
$k=2$
. By Lemma 2.6, this is impossible. Hence, by (4.1) and (4.5),
![]() $(b,c) \not \equiv (1,5) \bmod 24$
and
$(b,c) \not \equiv (1,5) \bmod 24$
and
Now assume
![]() $ b \equiv 2 \bmod 3$
. Then we have (4.1), (4.2) and
$ b \equiv 2 \bmod 3$
. Then we have (4.1), (4.2) and
and
When
![]() $x_2>1$
and
$x_2>1$
and
![]() $y_2>1$
, we see from (4.7) and (4.10) that (2.1) has a solution
$y_2>1$
, we see from (4.7) and (4.10) that (2.1) has a solution
![]() $(X,Y,m,n)=(c^{z_2/2}, b, x_2, y_2)$
. Hence, by Lemma 2.5,
$(X,Y,m,n)=(c^{z_2/2}, b, x_2, y_2)$
. Hence, by Lemma 2.5,
![]() $(b,c) = (17,71)$
, for which a solution
$(b,c) = (17,71)$
, for which a solution
![]() $(x_1, y_1, z_1)$
is impossible since
$(x_1, y_1, z_1)$
is impossible since
![]() $z_1=1$
. So we have either
$z_1=1$
. So we have either
![]() $x_2=1$
or
$x_2=1$
or
![]() $y_2=1$
.
$y_2=1$
.
If
![]() $y_2=1$
, then from (4.7) and (4.10),
$y_2=1$
, then from (4.7) and (4.10),
Note that
![]() $x_2>1$
since
$x_2>1$
since
![]() $c^{z_2}>c$
.
$c^{z_2}>c$
.
Apply Lemma 2.3 to (4.11) to obtain
Further, by (4.2), (4.11) and (4.12),
whence we obtain
However, by (4.2), we have
![]() $b < \sqrt {c}$
. By Lemma 2.9, we can assume
$b < \sqrt {c}$
. By Lemma 2.9, we can assume
![]() $\max \{ b,c\}> 100$
, so by (4.11),
$\max \{ b,c\}> 100$
, so by (4.11),
![]() $2^{x_2} = c^{z_2} - b> c^2 - \sqrt {c} \ge 101^2 - \sqrt {101} > 10190$
, whence we get
$2^{x_2} = c^{z_2} - b> c^2 - \sqrt {c} \ge 101^2 - \sqrt {101} > 10190$
, whence we get
![]() $x_2 \ge 15$
. So we have
$x_2 \ge 15$
. So we have
![]() $2^{0.04 x_2} - 1 \ge 2^{0.6}-1> 1/2$
. By (4.14),
$2^{0.04 x_2} - 1 \ge 2^{0.6}-1> 1/2$
. By (4.14),
Therefore, by (4.11), (4.13) and (4.15), we have
![]() $3b> 2^{x_2} + b = c^{z_2} \ge c^2 > b^4$
, which is a contradiction. So we obtain
$3b> 2^{x_2} + b = c^{z_2} \ge c^2 > b^4$
, which is a contradiction. So we obtain
![]() $y_2>1$
. This implies
$y_2>1$
. This implies
By (4.16), (4.1), (4.7) and (4.8),
Recalling (4.16), (4.7) and (4.10), we have
where
![]() $v_2(n)$
is the greatest integer t such that
$v_2(n)$
is the greatest integer t such that
![]() $2^t \mid n$
. From (4.17), we see that
$2^t \mid n$
. From (4.17), we see that
![]() $r>s$
, so that in (4.2), we must have
$r>s$
, so that in (4.2), we must have
![]() $x_1 = s$
.
$x_1 = s$
.
Now we apply Lemma 2.13. Clearly
![]() $2< {c^{z_2/2}}/{4}$
(recall Lemma 2.9), so that applying Lemma 2.13 to (4.2), we find that we must have
$2< {c^{z_2/2}}/{4}$
(recall Lemma 2.9), so that applying Lemma 2.13 to (4.2), we find that we must have
so that
which is false for all positive s.
Thus, we have
![]() $b \not \equiv 2 \bmod 3$
. So
$b \not \equiv 2 \bmod 3$
. So
![]() $b \equiv 1 \bmod 3$
and (4.6) holds.
$b \equiv 1 \bmod 3$
and (4.6) holds.
Proof of Corollary 1.6.
First,
![]() $N(a,b,c)=2$
follows from Theorem 1.4. If
$N(a,b,c)=2$
follows from Theorem 1.4. If
![]() $z_1=z_2$
, then, recalling Lemma 2.7 and noting that
$z_1=z_2$
, then, recalling Lemma 2.7 and noting that
![]() $c \ne 35$
,
$c \ne 35$
,
![]() $133$
or
$133$
or
![]() $259$
, we must have
$259$
, we must have
![]() $b^{y_2} - 2^{x_1} = b^{y_1} - 2^{x_2}> 0$
, so that Lemma 2.1 gives
$b^{y_2} - 2^{x_1} = b^{y_1} - 2^{x_2}> 0$
, so that Lemma 2.1 gives
![]() $2 \nmid x_1 - x_2$
. Consideration modulo 3 shows that this requires
$2 \nmid x_1 - x_2$
. Consideration modulo 3 shows that this requires
![]() $2 \nmid y_1 - y_2$
and
$2 \nmid y_1 - y_2$
and
![]() $b \equiv 2 \bmod 3$
, contradicting Theorem 1.5. So
$b \equiv 2 \bmod 3$
, contradicting Theorem 1.5. So
![]() $z_1 \ne z_2$
, and by Theorem 1.4,
$z_1 \ne z_2$
, and by Theorem 1.4,
![]() $z_2>1$
.
$z_2>1$
.
5 The unlikelihood of counterexamples to Conjecture 1.7
We outline the algorithm used to justify Theorem 1.8.
For a given prime value of b and some small prime p (or small prime power), we will consider all solutions
![]() $(x_1, y_1, x_2, y_2, z_2)$
to
$(x_1, y_1, x_2, y_2, z_2)$
to
![]() $2^{x_1} + b^{y_1} \equiv c \bmod p$
and
$2^{x_1} + b^{y_1} \equiv c \bmod p$
and
![]() $2^{x_2} + b^{y_2} \equiv c^{z_2} \bmod p$
. Note that the exponents are defined modulo
$2^{x_2} + b^{y_2} \equiv c^{z_2} \bmod p$
. Note that the exponents are defined modulo
![]() $p-1$
.
$p-1$
.
When
![]() $b \equiv 13 \bmod 24$
and
$b \equiv 13 \bmod 24$
and
![]() $c \equiv 5 \bmod 24$
, we must have
$c \equiv 5 \bmod 24$
, we must have
![]() $x_1=2$
. From above,
$x_1=2$
. From above,
![]() $2 \mid y_1$
,
$2 \mid y_1$
,
![]() $2 \mid x_2$
,
$2 \mid x_2$
,
![]() $ 2 \nmid y_2$
,
$ 2 \nmid y_2$
,
![]() $2 \nmid z_2>1$
, and
$2 \nmid z_2>1$
, and
![]() $z_2$
divides the class number of
$z_2$
divides the class number of
![]() $\mathbb {Q} (-b)$
.
$\mathbb {Q} (-b)$
.
For a given
![]() $b \equiv 13 \bmod 24$
, we find all
$b \equiv 13 \bmod 24$
, we find all
![]() $z_2>1$
with
$z_2>1$
with
![]() $z_2$
odd and dividing the class number. Fix b and
$z_2$
odd and dividing the class number. Fix b and
![]() $z_2$
. For a given prime p, we consider each
$z_2$
. For a given prime p, we consider each
![]() $y_1 \bmod p-1$
with
$y_1 \bmod p-1$
with
![]() $y_1$
even. Define
$y_1$
even. Define
![]() $c \equiv 2^{2} + b^{y_1} \bmod p$
; for each value of
$c \equiv 2^{2} + b^{y_1} \bmod p$
; for each value of
![]() $x_2$
even and
$x_2$
even and
![]() $y_2$
odd modulo
$y_2$
odd modulo
![]() $p-1$
, we see if
$p-1$
, we see if
![]() $ 2^{x_2} + b^{y_2} \equiv c^{z_2} \bmod p$
. If there is a solution, we add
$ 2^{x_2} + b^{y_2} \equiv c^{z_2} \bmod p$
. If there is a solution, we add
![]() $(y_1,x_2,y_2)$
to a list of all possible solutions modulo this prime p. We now consider another small prime (or prime power) q. For each possible solution modulo p, we now see if there is a solution modulo q. If we are fortunate, there are no solutions modulo q that are consistent with a solution modulo p, in which case this choice of b and
$(y_1,x_2,y_2)$
to a list of all possible solutions modulo this prime p. We now consider another small prime (or prime power) q. For each possible solution modulo p, we now see if there is a solution modulo q. If we are fortunate, there are no solutions modulo q that are consistent with a solution modulo p, in which case this choice of b and
![]() $z_2$
cannot have any solutions. Otherwise, we add another prime r and see if any solutions are consistent modulo r. Often for a given b,
$z_2$
cannot have any solutions. Otherwise, we add another prime r and see if any solutions are consistent modulo r. Often for a given b,
![]() $z_2$
has no consistent solutions after checking a few primes (or prime powers). In rare instances, the program required up to fourteen primes or prime powers to eliminate all possible solutions for a given b and
$z_2$
has no consistent solutions after checking a few primes (or prime powers). In rare instances, the program required up to fourteen primes or prime powers to eliminate all possible solutions for a given b and
![]() $z_2$
, but we never needed primes exceeding 241.
$z_2$
, but we never needed primes exceeding 241.
For
![]() $b \equiv 13 \bmod 24$
and
$b \equiv 13 \bmod 24$
and
![]() $c \equiv 17 \bmod 24$
, we must have
$c \equiv 17 \bmod 24$
, we must have
![]() $x_2=2$
. The procedure is similar except that we now consider tuples
$x_2=2$
. The procedure is similar except that we now consider tuples
![]() $(x_1, y_1, y_2)$
. For
$(x_1, y_1, y_2)$
. For
![]() $b \equiv 1 \bmod 24$
, we cannot specify
$b \equiv 1 \bmod 24$
, we cannot specify
![]() $x_1$
and
$x_1$
and
![]() $x_2$
so there are many more cases to check, but the same essential algorithm can be used.
$x_2$
so there are many more cases to check, but the same essential algorithm can be used.
We used Maple® for some preprocessing, then used Sage® (in which we could access the Pari® class number command) for the calculations. Total calculation time was approximately 100 hours. See the last author’s website for programs and details.
In summary, we showed that for primes
![]() $b<10^9$
, there are no solutions
$b<10^9$
, there are no solutions
![]() $(x_1, y_1, z_1, x_2, y_2, z_2)$
outside those listed in Conjecture 1.7. Since
$(x_1, y_1, z_1, x_2, y_2, z_2)$
outside those listed in Conjecture 1.7. Since
![]() $c>b^2$
, we have
$c>b^2$
, we have
![]() $c>10^{18}$
. This concludes the demonstration of Theorem 1.8.
$c>10^{18}$
. This concludes the demonstration of Theorem 1.8.
In another direction, it is interesting to note that the case
![]() $(b,c) \equiv (13,17) \bmod 24$
requires the equation
$(b,c) \equiv (13,17) \bmod 24$
requires the equation
Note that if
![]() $y_2=1$
, then
$y_2=1$
, then
![]() $c=2^{x_1} + b^{y_1}> 4+b = c^{z_2}$
, which is impossible; note also that
$c=2^{x_1} + b^{y_1}> 4+b = c^{z_2}$
, which is impossible; note also that
![]() $z_2=1$
is impossible by Corollary 1.6.
$z_2=1$
is impossible by Corollary 1.6.
The conditions in (5.1) are extremely unlikely even without the extra consideration of an additional solution
![]() $(x_1, y_1, z_1)$
.
$(x_1, y_1, z_1)$
.
Acknowledgements
The authors are indebted to Reese Scott, who pointed out numerous lemmas that greatly shortened the proofs, handled one special case and suggested the idea of the algorithm discussed in Section 5. We also thank Takafumi Miyazaki for calling our attention to an error.