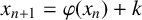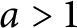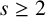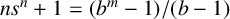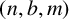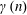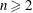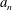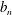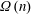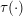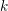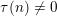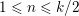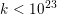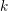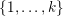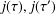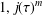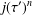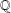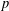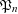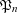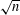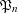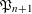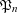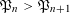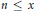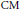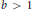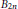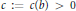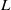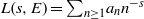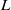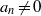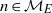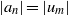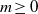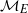54 results
ON THE ITERATES OF THE SHIFTED EULER’S FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 206-214
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Terms of Lucas sequences having a large smooth divisor
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 25 March 2022, pp. 225-231
- Print publication:
- March 2023
-
- Article
- Export citation
ON REPUNIT CULLEN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 264-268
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the prime factors of the iterates of the Ramanujan τ–function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 11 November 2020, pp. 1031-1047
-
- Article
- Export citation
Improving social function with real-world social-cognitive remediation in schizophrenia: Results from the RemedRugby quasi-experimental trial
-
- Journal:
- European Psychiatry / Volume 63 / Issue 1 / 2020
- Published online by Cambridge University Press:
- 30 April 2020, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Consecutive Integers with Close Kernels
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 24 October 2018, pp. 469-473
- Print publication:
- September 2019
-
- Article
- Export citation
Random ordering in modulus of consecutive Hecke eigenvalues of primitive forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 18 October 2018, pp. 2441-2461
- Print publication:
- November 2018
-
- Article
-
- You have access
- HTML
- Export citation
LINEAR INDEPENDENCE OF POWERS OF SINGULAR MODULI OF DEGREE THREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 12 September 2018, pp. 42-50
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
X-Ray Microscopy at Sirius, the New Brazilian Synchrotron Light Source
-
- Journal:
- Microscopy and Microanalysis / Volume 24 / Issue S2 / August 2018
- Published online by Cambridge University Press:
- 10 August 2018, pp. 172-175
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
On the typical size and cancellations among the coefficients of some modular forms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 166 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 19 April 2018, pp. 173-189
- Print publication:
- January 2019
-
- Article
- Export citation
A VARIATION ON THE THEME OF NICOMACHUS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 367-373
- Print publication:
- June 2018
-
- Article
-
- You have access
- Open access
- Export citation
DENOMINATORS OF BERNOULLI POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 16 April 2018, pp. 519-541
- Print publication:
- 2018
-
- Article
- Export citation
Interaction between the FTO gene, body mass index and depression: meta-analysis of 13701 individuals
-
- Journal:
- The British Journal of Psychiatry / Volume 211 / Issue 2 / August 2017
- Published online by Cambridge University Press:
- 02 January 2018, pp. 70-76
- Print publication:
- August 2017
-
- Article
-
- You have access
- HTML
- Export citation
ON POLYNOMIALS WHOSE ROOTS HAVE RATIONAL QUOTIENT OF DIFFERENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 185-190
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
MONOTONIC PHINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 365-372
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
FACTORIALS AND THE RAMANUJAN FUNCTION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 177-185
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
On the Counting Function of Elliptic Carmichael Numbers
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 1 / 14 March 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 105-112
- Print publication:
- 14 March 2014
-
- Article
-
- You have access
- Export citation
On the Sum of Digits of Numerators of Bernoulli Numbers
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 4 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 723-728
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
The clinical application of ABCB1 genotyping in antidepressant treatment: a pilot study
-
- Journal:
- CNS Spectrums / Volume 19 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 23 July 2013, pp. 165-175
-
- Article
- Export citation
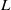 $L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
$L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 509-519
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation