Let 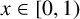G be a graph with no isolated vertex. A semitotal forcing set of G is a (zero) forcing set S such that every vertex in S is within distance 2 of another vertex of S. The semitotal forcing number $F_{t2}(G)$ is the minimum cardinality of a semitotal forcing set in G. In this paper, we prove that it is NP-complete to determine the semitotal forcing number of a graph. We also prove that if $G\neq K_n$ is a connected graph of order $n\geq 4$ with maximum degree $\Delta \geq 2$, then $F_{t2}(G)\leq (\Delta-1)n/\Delta$, with equality if and only if either $G=C_{4}$ or $G=P_{4}$ or $G=K_{\Delta ,\Delta }$.

Let $x\in [0,1)$ be an irrational number and let 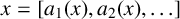$x=[a_{1}(x),a_{2}(x),\ldots ]$ be its continued fraction expansion with partial quotients 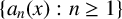$\{a_{n}(x): n\geq 1\}$. Given a natural number m and a vector 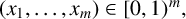$(x_{1},\ldots ,x_{m})\in [0,1)^{m},$ we derive the asymptotic behaviour of the shortest distance function

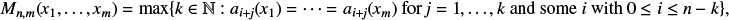$$ \begin{align*} M_{n,m}(x_{1},\ldots,x_{m})=\max\{k\in \mathbb{N}: a_{i+j}(x_{1})=\cdots= a_{i+j}(x_{m}) \ \text{for}~ j=1,\ldots,k \mbox{ and some } i \mbox{ with } 0\leq i \leq n-k\}, \end{align*} $$

which represents the run-length of the longest block of the same symbol among the first n partial quotients of $(x_{1},\ldots ,x_{m}).$ We also calculate the Hausdorff dimension of the level sets and exceptional sets arising from the shortest distance function.

Let $k\ge 2$ be an integer and let A be a set of nonnegative integers. The representation function $R_{A,k}(n)$ for the set A is the number of representations of a nonnegative integer n as the sum of k terms from A. Let $A(n)$ denote the counting function of A. Bell and Shallit [‘Counterexamples to a conjecture of Dombi in additive number theory’, Acta Math. Hung., to appear] recently gave a counterexample for a conjecture of Dombi and proved that if $A(n)=o(n^{{(k-2)}/{k}-\epsilon })$ for some $\epsilon>0$, then $R_{\mathbb {N}\setminus A,k}(n)$ is eventually strictly increasing. We improve this result to $A(n)=O(n^{{(k-2)}/{(k-1)}})$. We also give an example to show that this bound is best possible.

Let $\varphi $ be Euler’s function and fix an integer $k\ge 0$. We show that for every initial value $x_1\ge 1$, the sequence of positive integers $(x_n)_{n\ge 1}$ defined by $x_{n+1}=\varphi (x_n)+k$ for all $n\ge 1$ is eventually periodic. Similarly, for all initial values $x_1,x_2\ge 1$, the sequence of positive integers $(x_n)_{n\ge 1}$ defined by $x_{n+2}=\varphi (x_{n+1})+\varphi (x_n)+k$ for all $n\ge 1$ is eventually periodic, provided that k is even.

The integrality of the numbers $A_{n,m}={(2n)!(2m)!}/{n!m!(n+m)!}$ was observed by Catalan as early as 1874 and Gessel named $A_{n,m}$ the super Catalan numbers. The positivity of the q-super Catalan numbers (q-analogue of the super Catalan numbers) was investigated by Warnaar and Zudilin [‘A q-rious positivity’, Aequationes Math. 81 (2011), 177–183]. We prove the divisibility of sums of q-super Catalan numbers, which establishes a q-analogue of Apagodu’s congruence involving super Catalan numbers.

By examining two hypergeometric series transformations, we establish several remarkable infinite series identities involving harmonic numbers and quintic central binomial coefficients, including five conjectured recently by Z.-W. Sun [‘Series with summands involving harmonic numbers’, Preprint, 2023, arXiv:2210.07238v7]. This is realised by ‘the coefficient extraction method’ implemented by Mathematica commands.

For $k\geq 2$ and a nonzero integer n, a generalised Diophantine m-tuple with property $D_k(n)$ is a set of m positive integers $S = \{a_1,a_2,\ldots , a_m\}$ such that $a_ia_j + n$ is a kth power for $1\leq i< j\leq m$. Define $M_k(n):= \text {sup}\{|S| : S$ having property $D_k(n)\}$. Dixit et al. [‘Generalised Diophantine m-tuples’, Proc. Amer. Math. Soc. 150(4) (2022), 1455–1465] proved that $M_k(n)=O(\log n)$, for a fixed k, as n varies. In this paper, we obtain effective upper bounds on $M_k(n)$. In particular, we show that for $k\geq 2$, $M_k(n) \leq 3\,\phi (k) \log n$ if n is sufficiently large compared to k.

Let G be a semiabelian variety defined over an algebraically closed field K of prime characteristic. We describe the intersection of a subvariety X of G with a finitely generated subgroup of $G(K)$.

Formulas evaluating differences of integer partitions according to the parity of the parts are referred to as Legendre theorems. In this paper we give some formulas of Legendre type for overpartitions.

In 2019, Andrews and Newman [‘Partitions and the minimal excludant’, Ann. Comb. 23(2) (2019), 249–254] introduced the arithmetic function $\sigma \textrm {mex}(n)$, which denotes the sum of minimal excludants over all the partitions of n. Baruah et al. [‘A refinement of a result of Andrews and Newman on the sum of minimal excludants’, Ramanujan J., to appear] showed that the sum of minimal excludants over all the partitions of n is the same as the number of partition pairs of n into distinct parts. They proved three congruences modulo $4$ and $8$ for two functions appearing in this refinement and conjectured two further congruences modulo $8$ and $16$. We confirm these two conjectures by using q-series manipulations and modular forms.

We prove an upper bound for the sum of values of the ideal class zeta-function over nontrivial zeros of the Riemann zeta-function. The same result for the Dedekind zeta-function is also obtained. This may shed light on some unproved cases of the general Dedekind conjecture.

We study plane curves over finite fields whose tangent lines at smooth $\mathbb {F}_q$-points together cover all the points of $\mathbb {P}^2(\mathbb {F}_q)$.

As an extension of Sylvester’s matrix, a tridiagonal matrix is investigated by determining both left and right eigenvectors. Orthogonality relations between left and right eigenvectors are derived. Two determinants of the matrices constructed by the left and right eigenvectors are evaluated in closed form.

The Frobenius–Schur indicators of characters in a real $2$-block with dihedral defect groups have been determined by Murray [‘Real subpairs and Frobenius–Schur indicators of characters in 2-blocks’, J. Algebra 322 (2009), 489–513]. We show that two infinite families described in his work do not exist and we construct examples for the remaining families. We further present some partial results on Frobenius–Schur indicators of characters in other tame blocks.

In this paper, we investigate finite solvable tidy groups. We prove that a solvable group with order divisible by at least two primes is tidy if all of its Hall subgroups that are divisible by only two primes are tidy.

An example of a nonfinitely based involution monoid of order five has recently been discovered. We confirm that this example is, up to isomorphism, the unique smallest among all involution monoids.

Let $\mathcal {K}_u$ denote the class of all analytic functions f in the unit disk $\mathbb {D}:=\{z\in \mathbb {C}:|z|<1\}$, normalised by $f(0)=f'(0)-1=0$ and satisfying $|zf'(z)/g(z)-1|<1$ in $\mathbb {D}$ for some starlike function g. Allu, Sokól and Thomas [‘On a close-to-convex analogue of certain starlike functions’, Bull. Aust. Math. Soc. 108 (2020), 268–281] obtained a partial solution for the Fekete–Szegö problem and initial coefficient estimates for functions in $\mathcal {K}_u$, and posed a conjecture in this regard. We prove this conjecture regarding the sharp estimates of coefficients and solve the Fekete–Szegö problem completely for functions in the class $\mathcal {K}_u$.

We introduce a technique that is helpful in evaluating the reflexivity index of several classes of topological spaces and lattices. The main results are related to products: we give a sufficient condition for the product of a topological space and a nest of balls to have low reflexivity index and determine the reflexivity index of all compact connected 2-manifolds.

By defining and applying the restricted topology, we have investigated certain connections between the boundary spectrum, the exponential spectrum, the topological boundary of the spectrum and the connected hull of the spectrum (see Mouton and Harte [‘Linking the boundary and exponential spectra via the restricted topology’, J. Math. Anal. Appl. 454 (2017), 730–745]). We now solve a remaining problem regarding the restricted connected hull.

We derive conditions for recurrence and transience for time-inhomogeneous birth-and-death processes considered as random walks with positively biased drifts. We establish a general result, from which the earlier known particular results by Menshikov and Volkov [‘Urn-related random walk with drift $\rho x^\alpha /t^\beta $’, Electron. J. Probab. 13 (2008), 944–960] follow.