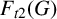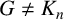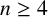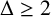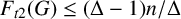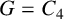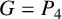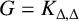1 Introduction
Forcing and its variations in graphs are now well studied. The (zero) forcing number of a graph was first introduced by the AIM Minimum Rank–Special Graphs Work Group [Reference Barioli, Barrett, Butler, Cioabǎ, Cvetković, Fallat, Godsil, Haemers, Hogben, Mikkelson, Narayan, Pryporova, Sciriha, So, Stevanović, van der Holst, Meulen and Wangsness2] to bound the maximum nullity/minimum rank of the family of symmetric matrices associated with a graph. Total forcing and semitotal forcing are two variations of forcing, which were first introduced and studied by Davila and Kenter [Reference Davila and Kenter8] and Chen [Reference Chen6]. The definitions are as follows.
For any two-colouring of the vertex set V of a graph G, say black and white for the two colours, define the colour-change rule: a white vertex v is converted to black if it is the only white neighbour of some black vertex
![]() $u$
. We say
$u$
. We say
![]() $u$
forces
$u$
forces
![]() $v$
, written
$v$
, written
![]() $u\rightarrow v$
, and also that u is a forcing vertex. Let S be a subset of V. Define a two-colouring of G by colouring S black and all other vertices white. The derived set
$u\rightarrow v$
, and also that u is a forcing vertex. Let S be a subset of V. Define a two-colouring of G by colouring S black and all other vertices white. The derived set
![]() $D(S)$
of S is the set of black vertices obtained by iteratively applying the colour-change rule until no more changes are possible. If
$D(S)$
of S is the set of black vertices obtained by iteratively applying the colour-change rule until no more changes are possible. If
![]() $D(S)=V$
, then we say S is a forcing set (also called a zero forcing set) of G. The procedure of colouring a graph using the colour-change rule applied to S is called a forcing process with respect to S. A minimum forcing set of G is a forcing set of G of minimum cardinality and the forcing number, denoted by
$D(S)=V$
, then we say S is a forcing set (also called a zero forcing set) of G. The procedure of colouring a graph using the colour-change rule applied to S is called a forcing process with respect to S. A minimum forcing set of G is a forcing set of G of minimum cardinality and the forcing number, denoted by
![]() $F(G)$
, is the cardinality of a minimum forcing set. If S is a forcing set of G and
$F(G)$
, is the cardinality of a minimum forcing set. If S is a forcing set of G and
![]() $G[S]$
contains no isolated vertex, then S is a total forcing set of G; if S is a forcing set of G and every vertex in S is within distance 2 of another vertex of S, then S is a semitotal forcing set of G. The total forcing number (respectively, semitotal forcing number) of G is the cardinality of a minimum total forcing set (respectively, semitotal forcing set) in G and denoted by
$G[S]$
contains no isolated vertex, then S is a total forcing set of G; if S is a forcing set of G and every vertex in S is within distance 2 of another vertex of S, then S is a semitotal forcing set of G. The total forcing number (respectively, semitotal forcing number) of G is the cardinality of a minimum total forcing set (respectively, semitotal forcing set) in G and denoted by
![]() $F_{t}(G)$
(respectively,
$F_{t}(G)$
(respectively,
![]() $F_{t2}(G)$
).
$F_{t2}(G)$
).
Determining the forcing number and the total forcing number for a graph are NP-complete (see [Reference Aazami1, Reference Chekuri, Korula, Albers, Marchetti-Spaccamela, Matias, Nikoletseas and Thomas5] and [Reference Davila and Henning7], respectively). Therefore, it is difficult to compute the forcing number or the total forcing number of a graph accurately and it is interesting to establish some bounds on these two parameters. Amos et al. [Reference Amos, Caro, Davila and Pepper3] proved
![]() $F(G)\leq {((\Delta -2)n+2)}/{(\Delta -1)}$
for a connected graph G of order n and maximum degree
$F(G)\leq {((\Delta -2)n+2)}/{(\Delta -1)}$
for a connected graph G of order n and maximum degree
![]() $\Delta \geq 2$
, with equality if and only if G is either
$\Delta \geq 2$
, with equality if and only if G is either
![]() $C_{n}, K_{n}$
or
$C_{n}, K_{n}$
or
![]() $K_{\Delta ,\Delta }$
(see Gentner et al. [Reference Gentner, Penso, Rautenbach and Souza9] and Lu et al. [Reference Lu, Wu and Tang11]). Caro and Pepper [Reference Caro and Pepper4] used a greedy algorithm to obtain an improved bound
$K_{\Delta ,\Delta }$
(see Gentner et al. [Reference Gentner, Penso, Rautenbach and Souza9] and Lu et al. [Reference Lu, Wu and Tang11]). Caro and Pepper [Reference Caro and Pepper4] used a greedy algorithm to obtain an improved bound
![]() $F(G)\leq {((\Delta -2)n-(\Delta -\delta )+2)}/{(\Delta -1)}$
, where
$F(G)\leq {((\Delta -2)n-(\Delta -\delta )+2)}/{(\Delta -1)}$
, where
![]() $\delta $
is the minimum degree of G. We gave a complete characterisation of the extremal graphs for this bound in [Reference Liang and Xu10]. For the total forcing number, Davila and Henning [Reference Davila and Henning7] showed that if G is a connected graph of order
$\delta $
is the minimum degree of G. We gave a complete characterisation of the extremal graphs for this bound in [Reference Liang and Xu10]. For the total forcing number, Davila and Henning [Reference Davila and Henning7] showed that if G is a connected graph of order
![]() $n\geq 3$
with maximum degree
$n\geq 3$
with maximum degree
![]() $\Delta \geq 2$
, then
$\Delta \geq 2$
, then
![]() $F_t(G)\leq {\Delta n}/{(\Delta +1)}$
, with equality if and only if
$F_t(G)\leq {\Delta n}/{(\Delta +1)}$
, with equality if and only if
![]() $G= K_{\Delta +1}$
or
$G= K_{\Delta +1}$
or
![]() $K_{1,\Delta }$
.
$K_{1,\Delta }$
.
In this paper, we study the semitotal forcing number of a graph. In Section 2, we give some basic definitions as preliminaries. In Section 3, we prove that it is NP-complete to determine the semitotal forcing number of a graph. In Section 4, we provide some upper bounds on the semitotal forcing number of a graph in terms of its order and maximum degree.
2 Preliminaries
Throughout this paper, we only consider simple, undirected and finite graphs.
Let
![]() $G=(V(G),E(G))$
be a graph with vertex set
$G=(V(G),E(G))$
be a graph with vertex set
![]() $V(G)$
and edge set
$V(G)$
and edge set
![]() $E(G)$
. Let
$E(G)$
. Let
![]() $u, v$
be two vertices of G. If
$u, v$
be two vertices of G. If
![]() $uv\in E(G)$
, then we say u, v are adjacent, u is a neighbour of v and vice versa. The open neighbourhood of v is
$uv\in E(G)$
, then we say u, v are adjacent, u is a neighbour of v and vice versa. The open neighbourhood of v is
![]() $N_G(v)=\{u\in V(G) \mid uv\in E(G)\}$
and the closed neighbourhood of v is
$N_G(v)=\{u\in V(G) \mid uv\in E(G)\}$
and the closed neighbourhood of v is
![]() $N_G[v]=N_G(v)\cup \{v\}$
. Similarly, for any set
$N_G[v]=N_G(v)\cup \{v\}$
. Similarly, for any set
![]() $X\subseteq V(G)$
,
$X\subseteq V(G)$
,
![]() $N_G(X)={\cup }_{v\in X}N_G(v)$
and
$N_G(X)={\cup }_{v\in X}N_G(v)$
and
![]() $N_G[X]=N_G(X)\cup X$
. The degree
$N_G[X]=N_G(X)\cup X$
. The degree
![]() $d_{G}(v)$
of v is the number of vertices in
$d_{G}(v)$
of v is the number of vertices in
![]() $N_{G}(v)$
. The minimum degree and maximum degree of G are denoted by
$N_{G}(v)$
. The minimum degree and maximum degree of G are denoted by
![]() $\delta (G)$
and
$\delta (G)$
and
![]() $\Delta (G)$
, respectively. We call a path connecting u and v a
$\Delta (G)$
, respectively. We call a path connecting u and v a
![]() $(u,v)$
-path. The distance between u and v is the length of a shortest
$(u,v)$
-path. The distance between u and v is the length of a shortest
![]() $(u,v)$
-path in G, denoted by
$(u,v)$
-path in G, denoted by
![]() $d_{G}(u,v)$
. For a vertex v and a vertex set X, let
$d_{G}(u,v)$
. For a vertex v and a vertex set X, let
![]() $d_{G}(v,X)=\min \{d_{G}(u,v) \mid u\in X\}$
. If the graph G is clear from the context, we write V, E,
$d_{G}(v,X)=\min \{d_{G}(u,v) \mid u\in X\}$
. If the graph G is clear from the context, we write V, E,
![]() $N(v)$
,
$N(v)$
,
![]() $N[v]$
,
$N[v]$
,
![]() $N(X)$
,
$N(X)$
,
![]() $N[X]$
,
$N[X]$
,
![]() $d(v)$
,
$d(v)$
,
![]() $\delta $
,
$\delta $
,
![]() $\Delta $
,
$\Delta $
,
![]() $d(u,v)$
,
$d(u,v)$
,
![]() $d(v,X)$
for short.
$d(v,X)$
for short.
An independent set of a graph is a set of pairwise nonadjacent vertices, whereas a clique of a graph is a set of pairwise adjacent vertices. A dominating set in a graph G is a set D of vertices of G such that every vertex not in D is adjacent to at least one vertex in D. For a set of vertices
![]() $X\subseteq V(G)$
, the induced subgraph by X, denoted by
$X\subseteq V(G)$
, the induced subgraph by X, denoted by
![]() $G[X]$
, is the graph with vertex set X, in which two vertices are adjacent if and only if they are adjacent in G. We denote by
$G[X]$
, is the graph with vertex set X, in which two vertices are adjacent if and only if they are adjacent in G. We denote by
![]() $G-X$
the induced subgraph
$G-X$
the induced subgraph
![]() $G[V\setminus X]$
; if
$G[V\setminus X]$
; if
![]() $X=\{x\}$
, we write
$X=\{x\}$
, we write
![]() $G-x$
for short.
$G-x$
for short.
Denote a path, a cycle and a complete graph on n vertices by
![]() $P_n$
,
$P_n$
,
![]() $C_n$
and
$C_n$
and
![]() $K_n$
, respectively. A complete bipartite graph with parts of sizes a and b is denoted
$K_n$
, respectively. A complete bipartite graph with parts of sizes a and b is denoted
![]() $K_{a,b}$
.
$K_{a,b}$
.
Two vertices u and v in a nontrivial connected graph G are twins if u and v have the same neighbours in
![]() $V(G)\setminus \{u,v\}$
.
$V(G)\setminus \{u,v\}$
.
Observation 2.1. If u and v are twins of a connected graph G, then every forcing set of G contains at least one vertex of
![]() $\{u,v\}$
.
$\{u,v\}$
.
3 Complexity of semitotal forcing
In this section, we show that the semitotal forcing problem is NP-complete. The decision version of the semitotal forcing problem is as follows.
Problem 3.1 (Semitotal Forcing)
Instance: a graph
![]() $G=(V,E)$
of order n and a positive integer
$G=(V,E)$
of order n and a positive integer
![]() $k\leq n$
. Question: does G have a semitotal forcing set of size at most k?
$k\leq n$
. Question: does G have a semitotal forcing set of size at most k?
Theorem 3.2. The semitotal forcing problem is NP-complete.
Proof. We first show that the semitotal forcing problem is in NP. Given a set S of vertices of G, it can be checked in polynomial time whether there is a vertex in S with exactly one neighbour not in S. Moreover, there cannot be more than
![]() $|V|$
steps in a forcing process. Thus, a nondeterministic algorithm can check in polynomial time whether a subset of vertices of V is forcing and further semitotal forcing, and whether it has size at most
$|V|$
steps in a forcing process. Thus, a nondeterministic algorithm can check in polynomial time whether a subset of vertices of V is forcing and further semitotal forcing, and whether it has size at most
![]() $k+1$
.
$k+1$
.
To show the hardness, we give a polynomial reduction from the forcing problem, which has been shown to be NP-complete in [Reference Aazami1, Reference Chekuri, Korula, Albers, Marchetti-Spaccamela, Matias, Nikoletseas and Thomas5].
Let
![]() $G=(V,E)$
be a graph, where
$G=(V,E)$
be a graph, where
![]() $V=\{v_1,\ldots , v_n\}$
. We construct a connected graph
$V=\{v_1,\ldots , v_n\}$
. We construct a connected graph
![]() $G'=(V',E')$
with vertex set
$G'=(V',E')$
with vertex set
![]() $V'=V\cup \{u,w_1,w_2\}$
and edge set
$V'=V\cup \{u,w_1,w_2\}$
and edge set
We will show that G has a forcing set of size at most k if and only if
![]() $G'$
has a semitotal forcing set of size at most k.
$G'$
has a semitotal forcing set of size at most k.
Suppose that G has a forcing set S of size at most k. We claim that
![]() $S'=S\cup \{w_1\}$
is a semitotal forcing set of
$S'=S\cup \{w_1\}$
is a semitotal forcing set of
![]() $G'$
. First, we colour all vertices in
$G'$
. First, we colour all vertices in
![]() $S'$
black and the other vertices of
$S'$
black and the other vertices of
![]() $G'$
white. Then
$G'$
white. Then
![]() $w_1\rightarrow u$
and further all vertices of
$w_1\rightarrow u$
and further all vertices of
![]() $V(G)$
can be forced by applying the colour-change rule to S. Finally,
$V(G)$
can be forced by applying the colour-change rule to S. Finally,
![]() $u\rightarrow w_2$
. Hence,
$u\rightarrow w_2$
. Hence,
![]() $S'$
is a forcing set of
$S'$
is a forcing set of
![]() $G'$
. Since every vertex in S is within distance 2 of the vertex
$G'$
. Since every vertex in S is within distance 2 of the vertex
![]() $w_1$
,
$w_1$
,
![]() $S'$
is a semitotal forcing set of
$S'$
is a semitotal forcing set of
![]() $G'$
of size at most
$G'$
of size at most
![]() $k+1$
.
$k+1$
.
Conversely, suppose that
![]() $G'$
has a semitotal forcing set
$G'$
has a semitotal forcing set
![]() $S'$
of size at most
$S'$
of size at most
![]() $k+1$
. By Observation 2.1, at least one vertex of
$k+1$
. By Observation 2.1, at least one vertex of
![]() $\{w_1, w_2\}$
belongs to
$\{w_1, w_2\}$
belongs to
![]() $S'$
. Renaming vertices if necessary, we may assume that
$S'$
. Renaming vertices if necessary, we may assume that
![]() $w_1\in S'$
. We can choose a semitotal forcing set
$w_1\in S'$
. We can choose a semitotal forcing set
![]() $S'$
such that u does not force any vertex of
$S'$
such that u does not force any vertex of
![]() $V(G)$
. This is because if u forces a vertex v of
$V(G)$
. This is because if u forces a vertex v of
![]() $V(G)$
, then
$V(G)$
, then
![]() $w_2\in S'$
, and
$w_2\in S'$
, and
![]() $S"=(S'\setminus\{w_2\}) \cup\{v\}$
is also a semitotal forcing set of
$S"=(S'\setminus\{w_2\}) \cup\{v\}$
is also a semitotal forcing set of
![]() $G'$
. Thus, each force between vertices of
$G'$
. Thus, each force between vertices of
![]() $V(G)$
in
$V(G)$
in
![]() $G'$
can also be applied for
$G'$
can also be applied for
![]() $S:= S'\cap V(G)$
in G, since if
$S:= S'\cap V(G)$
in G, since if
![]() $v\in V(G)$
has a single white neighbour in
$v\in V(G)$
has a single white neighbour in
![]() $G'$
at some step of the forcing process, it will have the same white neighbour in G. Moreover, since u does not force any vertex in
$G'$
at some step of the forcing process, it will have the same white neighbour in G. Moreover, since u does not force any vertex in
![]() $V(G)$
, all vertices in
$V(G)$
, all vertices in
![]() $V(G)$
must be forced by the vertices of
$V(G)$
must be forced by the vertices of
![]() $S'$
which are in
$S'$
which are in
![]() $V(G)$
. Thus, S is a forcing set of G. Additionally,
$V(G)$
. Thus, S is a forcing set of G. Additionally,
![]() $|S|= |S'\cap V(G)|\leq k+1-1=k$
, so S has size at most k.
$|S|= |S'\cap V(G)|\leq k+1-1=k$
, so S has size at most k.
4 General upper bounds
We emphasise that it is NP-hard to compute the semitotal forcing number for a general graph, so it is particularly interesting to find efficient bounds for the semitotal forcing number. In this section, we give some upper bounds on the semitotal forcing number of a graph in terms of its order and maximum degree. We use the following result.
Theorem 4.1 (Davila and Henning, [Reference Davila and Henning7]).
If G is a connected graph of order
![]() $n \geq 3$
with maximum degree
$n \geq 3$
with maximum degree
![]() $\Delta \geq 2$
, then
$\Delta \geq 2$
, then
with equality if and only if
![]() $G= K_{n}$
or
$G= K_{n}$
or
![]() $G=K_{1,n-1}$
.
$G=K_{1,n-1}$
.
Since every total forcing set is also a semitotal forcing set, we have the consequence.
Corollary 4.2. If G is a connected graph of order
![]() $n \geq 3$
with maximum degree
$n \geq 3$
with maximum degree
![]() $\Delta \geq 2$
, then
$\Delta \geq 2$
, then
with equality if and only if
![]() $G= K_{n}$
or
$G= K_{n}$
or
![]() $G=P_{3}$
.
$G=P_{3}$
.
We will give two improved upper bounds for the semitotal forcing number.
We define a weak partition
![]() $(V_1, \ldots , V_k)$
of the set V as a partition where some of the sets may be empty. Algorithm 1 outputs a weak partition of the vertex set V of G. According to Algorithm 1, lines 3–8 iteratively find a pair of vertices u and v with distance 2 in the current graph
$(V_1, \ldots , V_k)$
of the set V as a partition where some of the sets may be empty. Algorithm 1 outputs a weak partition of the vertex set V of G. According to Algorithm 1, lines 3–8 iteratively find a pair of vertices u and v with distance 2 in the current graph
![]() $G^{k-1}$
, set
$G^{k-1}$
, set
![]() $v_k=v$
and delete all vertices in
$v_k=v$
and delete all vertices in
![]() $N_{G^{k-1}}[N_{G^{k-1}}[v_k]]$
until the remaining connected components are complete graphs. Again, lines 10–14 iteratively delete the connected components whose order is greater than 2 in the remaining graph. Hence,
$N_{G^{k-1}}[N_{G^{k-1}}[v_k]]$
until the remaining connected components are complete graphs. Again, lines 10–14 iteratively delete the connected components whose order is greater than 2 in the remaining graph. Hence,
![]() $G[R]$
is a null graph or every component of
$G[R]$
is a null graph or every component of
![]() $G[R]$
is either an edge or an isolated vertex. For each vertex in
$G[R]$
is either an edge or an isolated vertex. For each vertex in
![]() $A\cup A'$
, its neighbours are in
$A\cup A'$
, its neighbours are in
![]() $B\cup B'\cup C$
. Thus, the set
$B\cup B'\cup C$
. Thus, the set
![]() $A\cup A'$
is independent. Similarly, for
$A\cup A'$
is independent. Similarly, for
![]() $1\leq i<j\leq r$
, there is no edge between
$1\leq i<j\leq r$
, there is no edge between
![]() $B_i$
and
$B_i$
and
![]() $B_j$
; and there is no edge between R and
$B_j$
; and there is no edge between R and
![]() $A\cup A'\cup B\cup B'$
.
$A\cup A'\cup B\cup B'$
.
We now restrict to
![]() $G\neq K_n$
. By using Algorithm 1, we present another upper bound on the semitotal forcing number of G in terms of its order and maximum degree.
$G\neq K_n$
. By using Algorithm 1, we present another upper bound on the semitotal forcing number of G in terms of its order and maximum degree.
Algorithm 1 Weak partition.

Theorem 4.3. If
![]() $G\neq K_n$
is a connected graph of order
$G\neq K_n$
is a connected graph of order
![]() $n \geq 4$
with maximum degree
$n \geq 4$
with maximum degree
![]() $\Delta \geq 2$
, then
$\Delta \geq 2$
, then
with equality if and only if
![]() $G=C_{4}$
or
$G=C_{4}$
or
![]() $G=P_{4}$
or
$G=P_{4}$
or
![]() $G=K_{\Delta ,\Delta }$
.
$G=K_{\Delta ,\Delta }$
.
Proof. Let
![]() $G\neq K_n$
be a connected graph of order
$G\neq K_n$
be a connected graph of order
![]() $n \geq 4$
with maximum degree
$n \geq 4$
with maximum degree
![]() $\Delta \geq 2$
. If
$\Delta \geq 2$
. If
![]() $\Delta =2$
, then
$\Delta =2$
, then
![]() $G=P_n$
or
$G=P_n$
or
![]() $G=C_n$
. In both cases,
$G=C_n$
. In both cases,
![]() $F_{t2}(G)=2\leq {n}/{2}= (\Delta-1)n/\Delta $
, as desired. Further, if
$F_{t2}(G)=2\leq {n}/{2}= (\Delta-1)n/\Delta $
, as desired. Further, if
![]() $F_{t2}(G)= (\Delta-1)n/\Delta$
, then
$F_{t2}(G)= (\Delta-1)n/\Delta$
, then
![]() $n = 4$
. Thus,
$n = 4$
. Thus,
![]() $G= C_4$
or
$G= C_4$
or
![]() $G = P_4$
. Hence, we assume that
$G = P_4$
. Hence, we assume that
![]() $\Delta \geq 3$
in what follows.
$\Delta \geq 3$
in what follows.
Applying Algorithm 1 to
![]() $G=(V,E)$
, we get a weak partition
$G=(V,E)$
, we get a weak partition
![]() $(A,B,C,A',B',R)$
of V, and
$(A,B,C,A',B',R)$
of V, and
![]() $A=\{v_1, \ldots , v_k\}$
,
$A=\{v_1, \ldots , v_k\}$
,
![]() $B=\{B_1, \ldots , B_k\}$
,
$B=\{B_1, \ldots , B_k\}$
,
![]() $C=\{C_1, \ldots , C_k\}$
,
$C=\{C_1, \ldots , C_k\}$
,
![]() $A'=\{v_{k+1}, \ldots , v_r\}$
,
$A'=\{v_{k+1}, \ldots , v_r\}$
,
![]() $B'=\{B_{k+1}, \ldots , B_r\}$
. Since
$B'=\{B_{k+1}, \ldots , B_r\}$
. Since
![]() $G\neq K_n$
, the sets A, B and C are not empty. For
$G\neq K_n$
, the sets A, B and C are not empty. For
![]() $1\leq i\leq k$
, let
$1\leq i\leq k$
, let
![]() $G_i$
be the graph induced by
$G_i$
be the graph induced by
![]() $\{v_i\}\cup B_i\cup C_i$
; for
$\{v_i\}\cup B_i\cup C_i$
; for
![]() $k+1\leq i\leq r$
, let
$k+1\leq i\leq r$
, let
![]() $G_i$
be the graph induced by
$G_i$
be the graph induced by
![]() $\{v_i\}\cup B_i$
. Note that r may be equal to k. Let
$\{v_i\}\cup B_i$
. Note that r may be equal to k. Let
![]() $G_i$
have order
$G_i$
have order
![]() $n_i$
and
$n_i$
and
![]() $|B_i| = b_i$
,
$|B_i| = b_i$
,
![]() $|C_i| = c_i$
. In what follows, we consider
$|C_i| = c_i$
. In what follows, we consider
![]() $G_i$
and divide into two cases.
$G_i$
and divide into two cases.
Case 1:
![]() $1\leq i\leq k$
. We divide into two subcases.
$1\leq i\leq k$
. We divide into two subcases.
Subcase 1.1:
![]() $b_i=1$
and
$b_i=1$
and
![]() $c_i=1$
. In this subcase,
$c_i=1$
. In this subcase,
![]() $G_i=P_3$
and
$G_i=P_3$
and
![]() $n_i=3$
. Let
$n_i=3$
. Let
![]() $S_i=\{v_i\}\cup B_i$
. Then
$S_i=\{v_i\}\cup B_i$
. Then
![]() $S_i$
is a semitotal forcing set of
$S_i$
is a semitotal forcing set of
![]() $G_i$
and
$G_i$
and
Subcase 1.2:
![]() $b_i\geq 2$
or
$b_i\geq 2$
or
![]() $c_i\geq 2$
. By Algorithm 1, we note that the set
$c_i\geq 2$
. By Algorithm 1, we note that the set
![]() $B_i$
dominates the set
$B_i$
dominates the set
![]() $C_i$
. Let
$C_i$
. Let
![]() $D_i$
be a minimum set of vertices in
$D_i$
be a minimum set of vertices in
![]() $B_i$
that dominate
$B_i$
that dominate
![]() $C_i$
and
$C_i$
and
![]() $|D_i| = d_i$
. Note that
$|D_i| = d_i$
. Note that
![]() $1 \leq d_i \leq b_i$
. Let
$1 \leq d_i \leq b_i$
. Let
![]() $D_{i}=\{x_1^i, \ldots , x_{d_i}^i\}$
. By the minimality of the set
$D_{i}=\{x_1^i, \ldots , x_{d_i}^i\}$
. By the minimality of the set
![]() $D_i$
, each vertex
$D_i$
, each vertex
![]() $x_j^i$
in
$x_j^i$
in
![]() $D_i$
dominates a vertex
$D_i$
dominates a vertex
![]() $y_j^i$
in
$y_j^i$
in
![]() $C_i$
that is not dominated by the other vertices in
$C_i$
that is not dominated by the other vertices in
![]() $D_i$
, where
$D_i$
, where
![]() $j\in [d_i]$
. Now, let
$j\in [d_i]$
. Now, let
![]() $D^{\prime }_i=\{y_1^i, \ldots , y_{d_i}^i\}$
and
$D^{\prime }_i=\{y_1^i, \ldots , y_{d_i}^i\}$
and
![]() $L_i=C_i\setminus D^{\prime }_i$
. Let
$L_i=C_i\setminus D^{\prime }_i$
. Let
![]() $|L_i|= l_i$
. Then
$|L_i|= l_i$
. Then
![]() $c_i= d_i + l_i$
and
$c_i= d_i + l_i$
and
![]() $n_i = b_i + c_i +1 = b_i + d_i + l_i + 1$
. Each vertex in
$n_i = b_i + c_i +1 = b_i + d_i + l_i + 1$
. Each vertex in
![]() $D_i$
is adjacent to
$D_i$
is adjacent to
![]() $v_i$
and to exactly one vertex in
$v_i$
and to exactly one vertex in
![]() $D^{\prime }_i$
, and therefore is adjacent to at most
$D^{\prime }_i$
, and therefore is adjacent to at most
![]() $\Delta - 2$
vertices in
$\Delta - 2$
vertices in
![]() $L_i$
, implying that
$L_i$
, implying that
![]() $l_i \leq d_i(\Delta - 2)$
. Let
$l_i \leq d_i(\Delta - 2)$
. Let
![]() $S_i= V(G_i)\setminus (D^{\prime }_i\cup \{x_1^i\})$
. By the construction,
$S_i= V(G_i)\setminus (D^{\prime }_i\cup \{x_1^i\})$
. By the construction,
![]() $S_i$
is semitotal. Further, the set
$S_i$
is semitotal. Further, the set
![]() $S_i$
is a forcing set of
$S_i$
is a forcing set of
![]() $G_i$
since
$G_i$
since
![]() $v_i\rightarrow x_1^i$
first, and then
$v_i\rightarrow x_1^i$
first, and then
![]() $x_j^i\rightarrow y_j^i$
for
$x_j^i\rightarrow y_j^i$
for
![]() $j\in [d_i]$
. Thus, the set
$j\in [d_i]$
. Thus, the set
![]() $S_i$
is a semitotal forcing set of
$S_i$
is a semitotal forcing set of
![]() $G_i$
. Moreover,
$G_i$
. Moreover,
 $$ \begin{align} |S_i|=b_i+ l_i &\leq b_i + d_i(\Delta-2) =b_i -d_i+ d_i(\Delta-1)\nonumber\\ &\leq \Delta-1+ d_i(\Delta-1) = (d_i+1)(\Delta-1), \end{align} $$
$$ \begin{align} |S_i|=b_i+ l_i &\leq b_i + d_i(\Delta-2) =b_i -d_i+ d_i(\Delta-1)\nonumber\\ &\leq \Delta-1+ d_i(\Delta-1) = (d_i+1)(\Delta-1), \end{align} $$
which implies that
![]() $d_i+1\geq |S_i|/(\Delta-1)$
. Thus,
$d_i+1\geq |S_i|/(\Delta-1)$
. Thus,
![]() $n_i=b_i+ l_i+d_i+1=|S_i|+d_i+1\geq |S_i|+|S_i|/(\Delta-1)$
and further
$n_i=b_i+ l_i+d_i+1=|S_i|+d_i+1\geq |S_i|+|S_i|/(\Delta-1)$
and further
![]() $|S_i|\leq (\Delta-1)n_i/\Delta$
.
$|S_i|\leq (\Delta-1)n_i/\Delta$
.
Case 2:
![]() $k+1\leq i\leq r$
. In this case,
$k+1\leq i\leq r$
. In this case,
![]() $G_i=G[\{v_i\}\cup \{B_i\}]$
is a complete graph. Since
$G_i=G[\{v_i\}\cup \{B_i\}]$
is a complete graph. Since
![]() $G\neq K_{\Delta +1}$
, we have
$G\neq K_{\Delta +1}$
, we have
![]() $2\leq b_i\leq \Delta -1$
. Let
$2\leq b_i\leq \Delta -1$
. Let
![]() $S_i= B_i$
. It is clear that
$S_i= B_i$
. It is clear that
![]() $S_i$
is a semitotal forcing set of
$S_i$
is a semitotal forcing set of
![]() $G_i$
. Thus,
$G_i$
. Thus,
![]() $n_i=b_i+1$
and
$n_i=b_i+1$
and
The set
![]() $S_i$
constructed for each
$S_i$
constructed for each
![]() $i\in [r]$
(see Cases 1 and 2 above) is a semitotal forcing set of
$i\in [r]$
(see Cases 1 and 2 above) is a semitotal forcing set of
![]() $G_i$
. We now let
$G_i$
. We now let
![]() $S'=\mathop {\cup }_{i=1}^{r} S_i$
. Thus,
$S'=\mathop {\cup }_{i=1}^{r} S_i$
. Thus,
 $$ \begin{align*} |S'|=\sum\limits_{i=1}^{r} |S_i|\leq\sum\limits_{i=1}^{r}\frac{\Delta-1}{\Delta}n_i =\frac{\Delta-1}{\Delta}\sum\limits_{i=1}^{r}n_i. \end{align*} $$
$$ \begin{align*} |S'|=\sum\limits_{i=1}^{r} |S_i|\leq\sum\limits_{i=1}^{r}\frac{\Delta-1}{\Delta}n_i =\frac{\Delta-1}{\Delta}\sum\limits_{i=1}^{r}n_i. \end{align*} $$
If
![]() $R=\emptyset $
, then
$R=\emptyset $
, then
![]() $V(G)=\mathop {\cup }_{i=1}^{r} V(G_i)$
. We claim that
$V(G)=\mathop {\cup }_{i=1}^{r} V(G_i)$
. We claim that
![]() $S=S'$
is a semitotal forcing set of G. As shown earlier, each set
$S=S'$
is a semitotal forcing set of G. As shown earlier, each set
![]() $S_i$
is a semitotal forcing set of
$S_i$
is a semitotal forcing set of
![]() $G_i$
for all
$G_i$
for all
![]() $i\in [r]$
. By the construction, S is semitotal. We colour all vertices in S black and the other vertices white. When we apply the colour-change rule, all vertices of
$i\in [r]$
. By the construction, S is semitotal. We colour all vertices in S black and the other vertices white. When we apply the colour-change rule, all vertices of
![]() $G_i$
will become black in the order i and
$G_i$
will become black in the order i and
 $$ \begin{align*} |S|=|S'|\leq\frac{\Delta-1}{\Delta}\sum\limits_{i=1}^{r}n_i=\frac{\Delta-1}{\Delta}n. \end{align*} $$
$$ \begin{align*} |S|=|S'|\leq\frac{\Delta-1}{\Delta}\sum\limits_{i=1}^{r}n_i=\frac{\Delta-1}{\Delta}n. \end{align*} $$
Now we consider
![]() $R\neq \emptyset $
. Suppose
$R\neq \emptyset $
. Suppose
![]() $G[R]$
has order
$G[R]$
has order
![]() $n_R$
. Recall that every component of
$n_R$
. Recall that every component of
![]() $G[R]$
is either an edge or an isolated vertex and there is no edge between R and
$G[R]$
is either an edge or an isolated vertex and there is no edge between R and
![]() $A\cup A'\cup B\cup B'$
. Since G is connected, every component of
$A\cup A'\cup B\cup B'$
. Since G is connected, every component of
![]() $G[R]$
is adjacent to some vertex of C. If there exists a vertex
$G[R]$
is adjacent to some vertex of C. If there exists a vertex
![]() $v\in R$
which is not adjacent to some vertex of C, then v belongs to a
$v\in R$
which is not adjacent to some vertex of C, then v belongs to a
![]() $P_2$
-component of
$P_2$
-component of
![]() $G[R]$
and its neighbour is adjacent to some vertex of C. Take all the vertices that are the same as v and put them into T. Let
$G[R]$
and its neighbour is adjacent to some vertex of C. Take all the vertices that are the same as v and put them into T. Let
![]() $|T|=t$
and
$|T|=t$
and
![]() $W=R\setminus T$
. Note that
$W=R\setminus T$
. Note that
![]() $W\neq \emptyset $
. Let
$W\neq \emptyset $
. Let
![]() $D\subseteq C$
be a minimum dominating set of W and
$D\subseteq C$
be a minimum dominating set of W and
![]() $|D|=d$
,
$|D|=d$
,
![]() $D=\{x_1,\ldots , x_d\}$
. By the minimality of the set D, each vertex
$D=\{x_1,\ldots , x_d\}$
. By the minimality of the set D, each vertex
![]() $x_j$
in D dominates a vertex
$x_j$
in D dominates a vertex
![]() $y_j$
in W that is not dominated by the other vertices in D, where
$y_j$
in W that is not dominated by the other vertices in D, where
![]() $j\in [d]$
. Let
$j\in [d]$
. Let
![]() $D'=\{y_1, \ldots , y_{d}\}$
and
$D'=\{y_1, \ldots , y_{d}\}$
and
![]() $L=W\setminus D'$
. Let
$L=W\setminus D'$
. Let
![]() $|L|= l$
so that
$|L|= l$
so that
![]() $n_R=d+l+t$
.
$n_R=d+l+t$
.
If
![]() $l=0$
, then
$l=0$
, then
![]() $S=S'$
is a semitotal forcing set of G. Additionally,
$S=S'$
is a semitotal forcing set of G. Additionally,
 $$ \begin{align*} |S|=|S'|\leq\frac{\Delta-1}{\Delta}\sum\limits_{i=1}^{r}n_i <\frac{\Delta-1}{\Delta}n. \end{align*} $$
$$ \begin{align*} |S|=|S'|\leq\frac{\Delta-1}{\Delta}\sum\limits_{i=1}^{r}n_i <\frac{\Delta-1}{\Delta}n. \end{align*} $$
Now assume that
![]() $l\neq 0$
. If
$l\neq 0$
. If
![]() $d(v, L\cup S')\leq 2$
for any
$d(v, L\cup S')\leq 2$
for any
![]() $v\in L$
, then set
$v\in L$
, then set
![]() $S"=L$
. Then
$S"=L$
. Then
![]() $S=S'\cup S"$
is a semitotal forcing set of G; we will justify this claim at the end of the proof. Since each vertex in
$S=S'\cup S"$
is a semitotal forcing set of G; we will justify this claim at the end of the proof. Since each vertex in
![]() $D\ (\subseteq C)$
is adjacent to a vertex of B and to exactly one vertex in
$D\ (\subseteq C)$
is adjacent to a vertex of B and to exactly one vertex in
![]() $D^{\prime }_i$
, we have
$D^{\prime }_i$
, we have
![]() $l\leq d(\Delta -2)$
. Recall that
$l\leq d(\Delta -2)$
. Recall that
![]() $n_R=d+l+t\geq d+l$
, so
$n_R=d+l+t\geq d+l$
, so
![]() $|S"|=l\leq d(\Delta -2)\leq (n_R-|S"|)(\Delta -2)$
. This implies that
$|S"|=l\leq d(\Delta -2)\leq (n_R-|S"|)(\Delta -2)$
. This implies that
![]() $|S"|\leq ({(\Delta -2)}/{(\Delta -1)})n_R< ({(\Delta -1)}/{\Delta })n_R$
. Thus,
$|S"|\leq ({(\Delta -2)}/{(\Delta -1)})n_R< ({(\Delta -1)}/{\Delta })n_R$
. Thus,
 $$ \begin{align*} \begin{aligned} |S|=|S'|+|S"| <\frac{\Delta-1}{\Delta}\sum\limits_{i=1}^{r}n_i+\frac{\Delta-1}{\Delta}n_R =\frac{\Delta-1}{\Delta}\bigg(\sum\limits_{i=1}^{r}n_i+n_R\bigg) =\frac{\Delta-1}{\Delta}n. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |S|=|S'|+|S"| <\frac{\Delta-1}{\Delta}\sum\limits_{i=1}^{r}n_i+\frac{\Delta-1}{\Delta}n_R =\frac{\Delta-1}{\Delta}\bigg(\sum\limits_{i=1}^{r}n_i+n_R\bigg) =\frac{\Delta-1}{\Delta}n. \end{aligned} \end{align*} $$
Suppose that there exists
![]() $v\in L$
such that
$v\in L$
such that
![]() $d(v, L\cup S')\geq 3$
. Take all the vertices that are the same as v and put them into X. For any
$d(v, L\cup S')\geq 3$
. Take all the vertices that are the same as v and put them into X. For any
![]() $w\in X$
, there exists
$w\in X$
, there exists
![]() $u\in D$
such that u is adjacent to w and
$u\in D$
such that u is adjacent to w and
![]() $u\in C_i$
for some i as in Subcase 1.2. Here, u is adjacent to
$u\in C_i$
for some i as in Subcase 1.2. Here, u is adjacent to
![]() $x_1^i$
, that is,
$x_1^i$
, that is,
![]() $u=y_1^i$
and
$u=y_1^i$
and
![]() $x_1^i$
is its neighbour in
$x_1^i$
is its neighbour in
![]() $G_i$
. Since
$G_i$
. Since
![]() $d(w, L\cup S')\geq 3$
, we have
$d(w, L\cup S')\geq 3$
, we have
![]() $N_{R}(y_1^i)=\{w,w'\}$
, where
$N_{R}(y_1^i)=\{w,w'\}$
, where
![]() $w'\in D'$
. Take all the vertices that are the same as
$w'\in D'$
. Take all the vertices that are the same as
![]() $w'$
and put them into Y. Now replace
$w'$
and put them into Y. Now replace
![]() $G_i$
with
$G_i$
with
![]() $G^{\prime }_i=G_i\cup \{w,w'\}$
and again divide into two cases. In the case
$G^{\prime }_i=G_i\cup \{w,w'\}$
and again divide into two cases. In the case
![]() $b_i\geq 2$
, we set
$b_i\geq 2$
, we set
![]() $x\in B_i\setminus \{x_1^i\}$
and
$x\in B_i\setminus \{x_1^i\}$
and
![]() $S^{\prime }_i=(S_i\setminus \{x\})\cup \{x_1^i,w\}$
. In the case
$S^{\prime }_i=(S_i\setminus \{x\})\cup \{x_1^i,w\}$
. In the case
![]() $b_i=1$
,
$b_i=1$
,
![]() $c_i\geq 2$
, clearly,
$c_i\geq 2$
, clearly,
![]() $D_i=\{x_1^i\}$
,
$D_i=\{x_1^i\}$
,
![]() $D^{\prime }_i=\{y_1^i\}$
and
$D^{\prime }_i=\{y_1^i\}$
and
![]() $L_i\neq \emptyset $
. Since
$L_i\neq \emptyset $
. Since
![]() $L_i\subseteq S_i$
, we set
$L_i\subseteq S_i$
, we set
![]() $y\in L_i$
and
$y\in L_i$
and
![]() $S^{\prime }_i=(S_i\setminus {y})\cup \{y_1^i,w\}$
. In both cases, it is not hard to check that
$S^{\prime }_i=(S_i\setminus {y})\cup \{y_1^i,w\}$
. In both cases, it is not hard to check that
![]() $S^{\prime }_i$
is a semitotal forcing set of
$S^{\prime }_i$
is a semitotal forcing set of
![]() $G^{\prime }_i$
. Then for
$G^{\prime }_i$
. Then for
![]() $G^{\prime }_i$
,
$G^{\prime }_i$
,
![]() $n^{\prime }_i=n_i+2=b_i+d_i+l_i+3$
and
$n^{\prime }_i=n_i+2=b_i+d_i+l_i+3$
and
![]() $|S^{\prime }_i|=|S_i|+1=b_i+ l_i+1\leq b_i + d_i(\Delta -2)+1={\kern1pt} b_i -d_i+ d_i(\Delta -1)+1\leq \Delta -1+ d_i(\Delta -1)+1{\kern1pt}={\kern1pt} (d_i+1)(\Delta -1)+1$
, which implies that
$|S^{\prime }_i|=|S_i|+1=b_i+ l_i+1\leq b_i + d_i(\Delta -2)+1={\kern1pt} b_i -d_i+ d_i(\Delta -1)+1\leq \Delta -1+ d_i(\Delta -1)+1{\kern1pt}={\kern1pt} (d_i+1)(\Delta -1)+1$
, which implies that
![]() $d_i+1\geq {(|S^{\prime }_i|-1)}/{(\Delta -1)}$
. Thus,
$d_i+1\geq {(|S^{\prime }_i|-1)}/{(\Delta -1)}$
. Thus,
 $n^{\prime }_i=b_i+ l_i+d_i+3=|S^{\prime }_i|+d_i+2\geq |S^{\prime }_i|+{(|S^{\prime }_i|-1)}/{(\Delta -1)}+1={(\Delta |S^{\prime }_i|+\Delta -2)}/{(\Delta -1)}> {\Delta |S^{\prime }_i|}/{(\Delta -1)}$
and further
$n^{\prime }_i=b_i+ l_i+d_i+3=|S^{\prime }_i|+d_i+2\geq |S^{\prime }_i|+{(|S^{\prime }_i|-1)}/{(\Delta -1)}+1={(\Delta |S^{\prime }_i|+\Delta -2)}/{(\Delta -1)}> {\Delta |S^{\prime }_i|}/{(\Delta -1)}$
and further
![]() $|S^{\prime }_i|<({(\Delta -1)}/{\Delta })n^{\prime }_i$
.
$|S^{\prime }_i|<({(\Delta -1)}/{\Delta })n^{\prime }_i$
.
Now return to W. Let
![]() $W'=W\setminus (X\cup Y)$
,
$W'=W\setminus (X\cup Y)$
,
![]() $D"=D'\setminus Y$
and
$D"=D'\setminus Y$
and
![]() $S"=L\setminus X$
. Let
$S"=L\setminus X$
. Let
![]() $R'=W'\cup T(=(D'\setminus Y)\cup (L\setminus X)\cup T)$
and
$R'=W'\cup T(=(D'\setminus Y)\cup (L\setminus X)\cup T)$
and
![]() $G_{R'}$
have order
$G_{R'}$
have order
![]() $n_{R'}$
. Then
$n_{R'}$
. Then
![]() $n_{R'}=d"+|S"|+t\geq d"+|S"|$
, where
$n_{R'}=d"+|S"|+t\geq d"+|S"|$
, where
![]() $d"=|D"|$
. Thus,
$d"=|D"|$
. Thus,
![]() $S=S'\cup S"$
is a semitotal forcing set of G, where some
$S=S'\cup S"$
is a semitotal forcing set of G, where some
![]() $S_i$
in
$S_i$
in
![]() $S'$
is replaced by
$S'$
is replaced by
![]() $S^{\prime }_i$
. We have
$S^{\prime }_i$
. We have
![]() $|S"|\leq (\Delta -2)d"\leq (\Delta -2)(n_{R'}-|S"|)= (\Delta -2)n_{R'}-(\Delta -2)|S"|$
. This implies
$|S"|\leq (\Delta -2)d"\leq (\Delta -2)(n_{R'}-|S"|)= (\Delta -2)n_{R'}-(\Delta -2)|S"|$
. This implies
![]() $|S"|\leq ({(\Delta -2)}/{(\Delta -1)})n_{R'}<({(\Delta -1)}/{\Delta })n_{R'}$
. Thus,
$|S"|\leq ({(\Delta -2)}/{(\Delta -1)})n_{R'}<({(\Delta -1)}/{\Delta })n_{R'}$
. Thus,
 $$ \begin{align*} \begin{aligned} |S|=|S'|+|S"| <\frac{\Delta-1}{\Delta}\sum\limits_{i=1}^{r}n_i+\frac{\Delta-1}{\Delta}n_{R'} =\frac{\Delta-1}{\Delta}\bigg(\sum\limits_{i=1}^{r}n_i+n_{R'}\bigg) =\frac{\Delta-1}{\Delta}n. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |S|=|S'|+|S"| <\frac{\Delta-1}{\Delta}\sum\limits_{i=1}^{r}n_i+\frac{\Delta-1}{\Delta}n_{R'} =\frac{\Delta-1}{\Delta}\bigg(\sum\limits_{i=1}^{r}n_i+n_{R'}\bigg) =\frac{\Delta-1}{\Delta}n. \end{aligned} \end{align*} $$
We now show that the set S is a semitotal forcing set in G. By the construction, S is semitotal. In the first stage of the forcing process, we colour all vertices in
![]() $G_i$
for
$G_i$
for
![]() $i\in [r]$
black. As shown earlier, when we apply the colour-change rule to
$i\in [r]$
black. As shown earlier, when we apply the colour-change rule to
![]() $S_i$
in
$S_i$
in
![]() $G_i$
with the order from small to large, all vertices of
$G_i$
with the order from small to large, all vertices of
![]() $G_i$
turn black.
$G_i$
turn black.
In the second stage of the forcing process, we colour all vertices of R black. Now we play each of the vertices of D in turn, thereby colouring all vertices in
![]() $D'$
black. Finally, all vertices of T can be forced and all vertices of G are coloured black.
$D'$
black. Finally, all vertices of T can be forced and all vertices of G are coloured black.
Thus,
![]() $F_{t2}(G)\leq |S|\leq ({(\Delta -1)}/{\Delta })n$
, as desired. Suppose next that
$F_{t2}(G)\leq |S|\leq ({(\Delta -1)}/{\Delta })n$
, as desired. Suppose next that
![]() $F_{t2}(G)= ({(\Delta -1)}/{\Delta })n$
. Then S is a minimum semitotal forcing set in G and
$F_{t2}(G)= ({(\Delta -1)}/{\Delta })n$
. Then S is a minimum semitotal forcing set in G and
![]() $|S|= ({(\Delta -1)}/{\Delta })n$
. Recall that by our earlier assumptions,
$|S|= ({(\Delta -1)}/{\Delta })n$
. Recall that by our earlier assumptions,
![]() $\Delta \geq 3$
. If
$\Delta \geq 3$
. If
![]() $R\neq \emptyset $
, then, as shown above,
$R\neq \emptyset $
, then, as shown above,
![]() $|S|< ({(\Delta -1)}/{\Delta })n$
, which is a contradiction. Hence,
$|S|< ({(\Delta -1)}/{\Delta })n$
, which is a contradiction. Hence,
![]() $R=\emptyset $
, implying that
$R=\emptyset $
, implying that
![]() $|S_i|=({(\Delta -1)}/{\Delta })n_i$
. For all
$|S_i|=({(\Delta -1)}/{\Delta })n_i$
. For all
![]() $i \in [k]$
, the set
$i \in [k]$
, the set
![]() $S_i$
must have been constructed as in Subcases 1.1 and 1.2 and equality holds in (4.1) and (4.2), which implies that (
$S_i$
must have been constructed as in Subcases 1.1 and 1.2 and equality holds in (4.1) and (4.2), which implies that (
![]() $\Delta =3$
,
$\Delta =3$
,
![]() $G_i=P_3$
) and (
$G_i=P_3$
) and (
![]() $b_i=\Delta $
,
$b_i=\Delta $
,
![]() $d_i=1$
,
$d_i=1$
,
![]() $l_i=\Delta -2$
), respectively.
$l_i=\Delta -2$
), respectively.
We claim that G is a regular graph. Otherwise,
![]() $\delta < \Delta $
and we can choose a weak partition
$\delta < \Delta $
and we can choose a weak partition
![]() $(A,B,C,A',B',R)$
of V such that
$(A,B,C,A',B',R)$
of V such that
![]() $v_1$
is a vertex of minimum degree. Thus,
$v_1$
is a vertex of minimum degree. Thus,
![]() $b_1\neq \Delta $
. Further,
$b_1\neq \Delta $
. Further,
![]() $\Delta =3$
and
$\Delta =3$
and
![]() $G_1=P_3$
, where
$G_1=P_3$
, where
![]() $d(v_1)=1$
. Let
$d(v_1)=1$
. Let
![]() $B_1=\{z\}$
. We find that
$B_1=\{z\}$
. We find that
![]() $d(z)=2$
. Now we reselect a weak partition
$d(z)=2$
. Now we reselect a weak partition
![]() $(A,B,C,A',B',R)$
of V such that
$(A,B,C,A',B',R)$
of V such that
![]() $v_1=z$
. Then
$v_1=z$
. Then
![]() $d(v_1)=b_i=2<\Delta $
and, by the previous analysis, equality holds in (4.1) and (4.2) for
$d(v_1)=b_i=2<\Delta $
and, by the previous analysis, equality holds in (4.1) and (4.2) for
![]() $i=1$
, which is a contradiction. Thus,
$i=1$
, which is a contradiction. Thus,
![]() $\delta =\Delta \geq 3$
.
$\delta =\Delta \geq 3$
.
Now consider
![]() $i=1$
. With
$i=1$
. With
![]() $S_1$
constructed as in Subcase 1.2, we have
$S_1$
constructed as in Subcase 1.2, we have
![]() $b_1=\Delta $
,
$b_1=\Delta $
,
![]() $d_1=1$
,
$d_1=1$
,
![]() $l_1=\Delta -2$
. Then,
$l_1=\Delta -2$
. Then,
![]() $d(v_1)=d(x_1^1)=\Delta $
. First, we show that
$d(v_1)=d(x_1^1)=\Delta $
. First, we show that
![]() $B_1$
is an independent set. Otherwise, there exist
$B_1$
is an independent set. Otherwise, there exist
![]() $u,v\in B_1$
different from
$u,v\in B_1$
different from
![]() $x_1$
such that u is adjacent to v. Since
$x_1$
such that u is adjacent to v. Since
![]() $\Delta $
is the maximum degree, there exists
$\Delta $
is the maximum degree, there exists
![]() $w\in C_1$
such that w is not adjacent to v. Let
$w\in C_1$
such that w is not adjacent to v. Let
![]() $S_1'=V(G_1)\setminus \{u,x_1,w\}$
. Then
$S_1'=V(G_1)\setminus \{u,x_1,w\}$
. Then
![]() $v\rightarrow u$
and further
$v\rightarrow u$
and further
![]() $v_1\rightarrow x_1^1\rightarrow w$
. Thus,
$v_1\rightarrow x_1^1\rightarrow w$
. Thus,
![]() $S_1'$
is a semitotal forcing set of
$S_1'$
is a semitotal forcing set of
![]() $G_1$
smaller than
$G_1$
smaller than
![]() $S_1$
, and so
$S_1$
, and so
![]() $(S\setminus S_1)\cup S_1'$
is a semitotal forcing set of G smaller than S, which is a contradiction. Since
$(S\setminus S_1)\cup S_1'$
is a semitotal forcing set of G smaller than S, which is a contradiction. Since
![]() $\Delta $
is the maximum degree, it is not hard to see that
$\Delta $
is the maximum degree, it is not hard to see that
![]() $N(v)=\{v_1\}\cup C_1$
for each
$N(v)=\{v_1\}\cup C_1$
for each
![]() $v\in B_1$
. Therefore,
$v\in B_1$
. Therefore,
![]() $G=K_{\Delta ,\Delta }$
, as desired.
$G=K_{\Delta ,\Delta }$
, as desired.
This completes the proof.
As an immediate consequence of Theorem 4.3, we have the following result.
Theorem 4.4. If G is a connected graph of order
![]() $n \geq 3$
with maximum degree
$n \geq 3$
with maximum degree
![]() $\Delta \geq 2$
, then
$\Delta \geq 2$
, then
with equality if and only if
![]() $G=K_{n}$
or
$G=K_{n}$
or
![]() $G=P_{3}$
.
$G=P_{3}$
.
Proof. Let G be a connected graph of order
![]() $n \geq 3$
with maximum degree
$n \geq 3$
with maximum degree
![]() $\Delta \geq 2$
. If
$\Delta \geq 2$
. If
![]() $G=K_n$
, then
$G=K_n$
, then
![]() $F_{t2}(G)=n-1= ({(\Delta -1)n+1})/{\Delta }$
. Now consider
$F_{t2}(G)=n-1= ({(\Delta -1)n+1})/{\Delta }$
. Now consider
![]() $G\neq K_n$
. If
$G\neq K_n$
. If
![]() $n=3$
, then
$n=3$
, then
![]() $G=P_3$
and
$G=P_3$
and
![]() $F_{t2}(G)=2= ({(\Delta -1)n+1})/{\Delta }$
, as desired. If
$F_{t2}(G)=2= ({(\Delta -1)n+1})/{\Delta }$
, as desired. If
![]() $n\geq 4$
, then
$n\geq 4$
, then
![]() $F_{t2}(G)\leq {(\Delta -1)n}/{\Delta }<({(\Delta -1)n+1})/{\Delta }$
by Theorem 4.3. Thus,
$F_{t2}(G)\leq {(\Delta -1)n}/{\Delta }<({(\Delta -1)n+1})/{\Delta }$
by Theorem 4.3. Thus,
![]() $F_{t2}(G)\leq ({(\Delta -1)n+1})/{\Delta }$
, with equality if and only if
$F_{t2}(G)\leq ({(\Delta -1)n+1})/{\Delta }$
, with equality if and only if
![]() $G=K_{n}$
or
$G=K_{n}$
or
![]() $G=P_{3}$
.
$G=P_{3}$
.
If G is a connected graph of order n with maximum degree
![]() $\Delta $
, then
$\Delta $
, then
![]() $n\geq \Delta + 1$
and
$n\geq \Delta + 1$
and
The equality holds in (4.3) if and only if
![]() $n = \Delta + 1$
. Thus,
$n = \Delta + 1$
. Thus,
![]() $F_{t2}(G)= ({(\Delta -1)n+1})/{\Delta }=\Delta n/(\Delta+1)$
if and only if
$F_{t2}(G)= ({(\Delta -1)n+1})/{\Delta }=\Delta n/(\Delta+1)$
if and only if
![]() $G=K_{n}$
or
$G=K_{n}$
or
![]() $G=P_{3}$
. Thus, the upper bound of Theorem 4.2 follows as an immediate consequence of the upper bound of Theorem 4.4.
$G=P_{3}$
. Thus, the upper bound of Theorem 4.2 follows as an immediate consequence of the upper bound of Theorem 4.4.