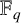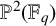Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ASGARLI, SHAMIL
and
GHIOCA, DRAGOS
2024.
TANGENT-FILLING PLANE CURVES OVER FINITE FIELDS.
Bulletin of the Australian Mathematical Society,
Vol. 109,
Issue. 2,
p.
301.