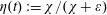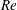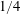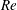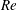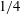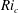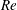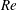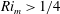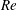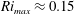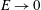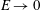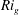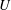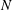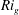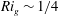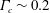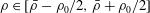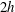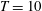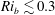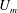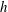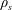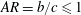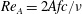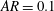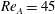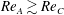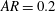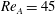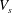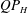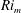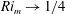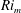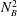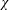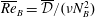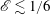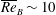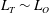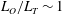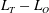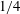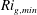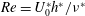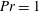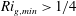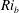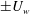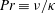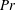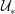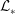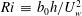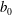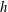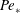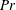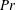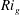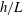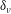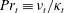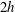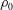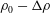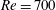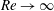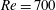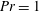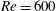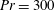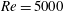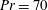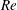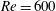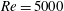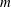68 results
The dynamics of stratified horizontal shear flows at low Péclet number
-
- Journal:
- Journal of Fluid Mechanics / Volume 903 / 25 November 2020
- Published online by Cambridge University Press:
- 17 September 2020, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mixing in forced stratified turbulence and its dependence on large-scale forcing
-
- Journal:
- Journal of Fluid Mechanics / Volume 898 / 10 September 2020
- Published online by Cambridge University Press:
- 25 June 2020, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The viscous Holmboe instability for smooth shear and density profiles
-
- Journal:
- Journal of Fluid Mechanics / Volume 896 / 10 August 2020
- Published online by Cambridge University Press:
- 01 June 2020, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kelvin–Helmholtz billows above Richardson number
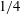 $1/4$
$1/4$
-
- Journal:
- Journal of Fluid Mechanics / Volume 879 / 25 November 2019
- Published online by Cambridge University Press:
- 23 September 2019, R1
-
- Article
- Export citation
Mixing and entrainment are suppressed in inclined gravity currents
-
- Journal:
- Journal of Fluid Mechanics / Volume 873 / 25 August 2019
- Published online by Cambridge University Press:
- 28 June 2019, pp. 786-815
-
- Article
- Export citation
Layer formation and relaminarisation in plane Couette flow with spanwise stratification
-
- Journal:
- Journal of Fluid Mechanics / Volume 868 / 10 June 2019
- Published online by Cambridge University Press:
- 10 April 2019, pp. 97-118
-
- Article
-
- You have access
- HTML
- Export citation
Self-organized criticality of turbulence in strongly stratified mixing layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 856 / 10 December 2018
- Published online by Cambridge University Press:
- 02 October 2018, pp. 228-256
-
- Article
- Export citation
Optimal mixing in two-dimensional stratified plane Poiseuille flow at finite Péclet and Richardson numbers
-
- Journal:
- Journal of Fluid Mechanics / Volume 853 / 25 October 2018
- Published online by Cambridge University Press:
- 23 August 2018, pp. 359-385
-
- Article
- Export citation
Optimal mixing in three-dimensional plane Poiseuille flow at high Péclet number
-
- Journal:
- Journal of Fluid Mechanics / Volume 850 / 10 September 2018
- Published online by Cambridge University Press:
- 10 July 2018, pp. 875-923
-
- Article
- Export citation
The structure and origin of confined Holmboe waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 848 / 10 August 2018
- Published online by Cambridge University Press:
- 05 June 2018, pp. 508-544
-
- Article
- Export citation
Horizontal locomotion of a vertically flapping oblate spheroid
-
- Journal:
- Journal of Fluid Mechanics / Volume 840 / 10 April 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 688-708
-
- Article
- Export citation
Testing linear marginal stability in stratified shear layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 839 / 25 March 2018
- Published online by Cambridge University Press:
- 02 February 2018, R4
-
- Article
- Export citation
Layer formation in horizontally forced stratified turbulence: connecting exact coherent structures to linear instabilities
-
- Journal:
- Journal of Fluid Mechanics / Volume 832 / 10 December 2017
- Published online by Cambridge University Press:
- 26 October 2017, pp. 409-437
-
- Article
-
- You have access
- HTML
- Export citation
Irreversible mixing by unstable periodic orbits in buoyancy dominated stratified turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 832 / 10 December 2017
- Published online by Cambridge University Press:
- 26 October 2017, R1
-
- Article
- Export citation
Role of overturns in optimal mixing in stratified mixing layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 826 / 10 September 2017
- Published online by Cambridge University Press:
- 08 August 2017, pp. 522-552
-
- Article
- Export citation
Nonlinear evolution of linear optimal perturbations of strongly stratified shear layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 825 / 25 August 2017
- Published online by Cambridge University Press:
- 20 July 2017, pp. 213-244
-
- Article
- Export citation
Diapycnal mixing in layered stratified plane Couette flow quantified in a tracer-based coordinate
-
- Journal:
- Journal of Fluid Mechanics / Volume 823 / 25 July 2017
- Published online by Cambridge University Press:
- 15 June 2017, pp. 198-229
-
- Article
- Export citation
Self-similar mixing in stratified plane Couette flow for varying Prandtl number
-
- Journal:
- Journal of Fluid Mechanics / Volume 820 / 10 June 2017
- Published online by Cambridge University Press:
- 04 May 2017, pp. 86-120
-
- Article
- Export citation
Multiple instability of layered stratified plane Couette flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 813 / 25 February 2017
- Published online by Cambridge University Press:
- 17 January 2017, pp. 250-278
-
- Article
- Export citation
Optimal perturbation growth in axisymmetric intrusions
-
- Journal:
- Journal of Fluid Mechanics / Volume 811 / 25 January 2017
- Published online by Cambridge University Press:
- 14 December 2016, R4
-
- Article
- Export citation