Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-26T20:17:56.172Z Has data issue: false hasContentIssue false
  • English
  • Français

Diapycnal mixing in layered stratified plane Couette flow quantified in a tracer-based coordinate

Published online by Cambridge University Press:  15 June 2017

Qi Zhou Open the ORCID record for Qi Zhou [Opens in a new window] ,
J. R. Taylor Open the ORCID record for J. R. Taylor [Opens in a new window] ,
C. P. Caulfield Open the ORCID record for C. P. Caulfield [Opens in a new window]  and
P. F. Linden
Qi Zhou*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
J. R. Taylor
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
C. P. Caulfield
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
P. F. Linden
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: q.zhou@damtp.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The mixing properties of statically stable density interfaces subject to imposed vertical shear are studied using direct numerical simulations of stratified plane Couette flow. The simulations are designed to investigate possible self-maintaining mechanisms of sharp density interfaces motivated by Phillips’ argument (Deep-Sea Res., vol. 19, 1972, pp. 79–81) by which layers and interfaces can spontaneously form due to vertical variations of diapycnal flux. At the start of each simulation, a sharp density interface with the same initial thickness is introduced at the midplane between two flat, horizontal walls counter-moving at velocities 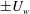$\pm U_{w}$. Particular attention is paid to the effects of varying Prandtl number 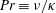$\mathit{Pr}\equiv \unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$, where $\unicode[STIX]{x1D708}$ and $\unicode[STIX]{x1D705}$ are the molecular kinematic viscosity and diffusivity respectively, over two orders of magnitude from 0.7, 7 and 70. Varying 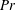$\mathit{Pr}$ enables the system to access a considerable range of characteristic turbulent Péclet numbers 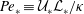$\mathit{Pe}_{\ast }\equiv {\mathcal{U}}_{\ast }{\mathcal{L}}_{\ast }/\unicode[STIX]{x1D705}$, where 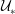${\mathcal{U}}_{\ast }$ and 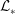${\mathcal{L}}_{\ast }$ are characteristic velocity and length scales, respectively, of the motion which acts to ‘scour’ the density interface. The dynamics of the interface varies with the stability of the interface which is characterised by a bulk Richardson number 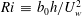$\mathit{Ri}\,\equiv \,b_{0}h/U_{w}^{2}$, where 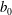$b_{0}$ is half the initial buoyancy difference across the interface and 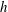$h$ is the half-height of the channel. Shear-induced turbulence occurs at small 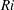$\mathit{Ri}$, whereas internal waves propagating on the interface dominate at large 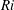$\mathit{Ri}$. For a highly stable (i.e. large 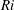$\mathit{Ri}$) interface at sufficiently large 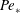$\mathit{Pe}_{\ast }$, the complex interfacial dynamics allows the interface to remain sharp. This ‘self-sharpening’ is due to the combined effects of the ‘scouring’ induced by the turbulence external to the interface and comparatively weak molecular diffusion across the core region of the interface. The effective diapycnal diffusivity and irreversible buoyancy flux are quantified in the tracer-based reference coordinate proposed by Winters & D’Asaro (J. Fluid Mech., vol. 317, 1996, pp. 179–193) and Nakamura (J. Atmos. Sci., vol. 53, 1996, pp. 1524–1537), which enables a detailed investigation of the self-sharpening process by analysing the local budget of buoyancy gradient in the reference coordinate. We further discuss the dependence of the effective diffusivity and overall mixing efficiency on the characteristic parameters of the flow, such as the buoyancy Reynolds number and the local gradient Richardson number, and highlight the possible role of the molecular properties of fluids on diapycnal mixing.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Mixing: Mixing Turbulent Flows: Stratified turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 823 , 25 July 2017 , pp. 198 - 229
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, P. G. & Mitsudera, H. 1994 On the mechanism of shear flow instabilities. J. Fluid Mech. 276, 327–342.CrossRefGoogle Scholar
Balmforth, N. J., Llewellyn-Smith, S. G. & Young, W. R. 1998 Dynamics of interfaces and layers in a stratified turbulent fluid. J. Fluid Mech. 355, 329–358.CrossRefGoogle Scholar
Bouffard, D. & Boegman, L. 2013 A diapycnal diffusivity model for stratified environmental flows. Dyn. Atmos. Oceans 61–62, 14–34.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.CrossRefGoogle Scholar
Carpenter, J. R., Balmforth, N. J. & Lawrence, G. A. 2010 Identifying unstable modes in stratified shear layers. Phys. Fluids 22, 054104.Google Scholar
Carpenter, J. R., Tedford, E. W., Heifetz, E. & Lawrence, G. A. 2011 Instability in stratified shear flow: review of a physical interpretation based on interacting waves. Appl. Mech. Rev. 64, 060801.Google Scholar
Caulfield, C.-C. P. 1994 Multiple instability of layered stratified shear flow. J. Fluid Mech. 258, 255–285.CrossRefGoogle Scholar
Caulfield, C. P. & Peltier, W. R. 2000 The anatomy of the mixing transition in homogeneous and stratified free shear layers. J. Fluid Mech. 413, 1–47.Google Scholar
Crapper, P. F. & Linden, P. F. 1974 The structure of turbulent density interfaces. J. Fluid Mech. 65, 45–63.CrossRefGoogle Scholar
Deusebio, E., Caulfield, C. P. & Taylor, J. R. 2015 The intermittency boundary in stratified plane Couette flow. J. Fluid Mech. 781, 298–329.CrossRefGoogle Scholar
Eaves, T. S. & Caulfield, C. P. 2017 Multiple instability of layered stratified plane Couette flow. J. Fluid Mech. 813, 250–278.Google Scholar
Eliassen, A., Hailand, E. & Riis, E. 1953 Two-dimensional Perturbation of a Flow with Constant Shear of a Stratified Fluid. Norwegian Academy of Sciences and Letters.Google Scholar
Fernando, H. J. S. 1991 Turbulent mixing in stratified fluids. Annu. Rev. Fluid Mech. 23, 455–493.CrossRefGoogle Scholar
Gregg, M. C. 1980 Microstructure patches in the thermocline. J. Phys. Oceanogr. 10, 915–943.2.0.CO;2>CrossRefGoogle Scholar
Linden, P. F. 1979 Mixing in stratified fluids. Geophys. Astrophys. Fluid Dyn. 13, 3–23.CrossRefGoogle Scholar
Maffioli, A., Brethouwer, G. & Lindborg, E. 2016 Mixing efficiency in stratified turbulence. J. Fluid Mech. 794, R3.CrossRefGoogle Scholar
Marshall, J., Shuckburgh, E., Jones, H. & Hill, C. 2006 Estimates and implications of surface eddy diffusivity in the southern ocean derived from tracer transport. J. Phys. Oceanogr. 36, 1806–1821.Google Scholar
Mashayek, A., Caulfield, C. P. & Peltier, W. R. 2013 Time-dependent, non-monotonic mixing in stratified turbulent shear flows: implications for oceanographic estimates of buoyancy flux. J. Fluid Mech. 736, 570–593.CrossRefGoogle Scholar
Mellor, G. L. & Yamada, T. 1982 Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 20, 851–875.Google Scholar
Nakamura, N. 1996 Two-dimensional mixing, edge formation, and permeability diagnosed in an area coordinate. J. Atmos. Sci. 53, 1524–1537.2.0.CO;2>CrossRefGoogle Scholar
Oglethorpe, R. L. F., Caulfield, C. P. & Woods, A. W. 2013 Spontaneous layering in stratified turbulent Taylor–Couette flow. J. Fluid Mech. 721, R3.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Phillips, O. M. 1972 Turbulence in a strongly stratified fluid – is it unstable? Deep-Sea Res. 19, 79–81.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Posmentier, E. S. 1977 The generation of salinity fine structure by vertical diffusion. J. Phys. Oceanogr. 7, 298–300.Google Scholar
Ruddick, B. R., McDougall, T. J. & Turner, J. S. 1989 The formation of layers in a uniformly stirred density gradient. Deep-Sea Res. 36, 597–609.CrossRefGoogle Scholar
Salehipour, H., Caulfield, C. P. & Peltier, W. R. 2016a Turbulent mixing due to the Holmboe wave instability at high Reynolds number. J. Fluid Mech. 803, 591–621.CrossRefGoogle Scholar
Salehipour, H. & Peltier, W. R. 2015 Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in Boussinesq stratified turbulence. J. Fluid Mech. 775, 464–500.Google Scholar
Salehipour, H., Peltier, W. R., Whalen, C. B. & MacKinnon, J. A. 2016b A new characterization of the turbulent diapycnal diffusivities of mass and momentum in the ocean. Geophys. Res. Lett. 43, 3370–3379.Google Scholar
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H. 2005 Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
Shuckburgh, E. & Haynes, P. 2003 Diagnosing transport and mixing using a tracer-based coordinate system. Phys. Fluids 15, 3342–3357.Google Scholar
Smyth, W. D., Klaassen, G. P. & Peltier, W. R. 1988 Finite amplitude Holmboe waves. Geophys. Astrophys. Fluid Dyn. 43, 181–222.Google Scholar
Smyth, W. D., Moum, J. & Caldwell, D. 2001 The efficiency of mixing in turbulent patches: inferences from direct simulations and microstructure observations. J. Phys. Oceanogr. 31, 1969–1992.Google Scholar
Smyth, W. D., Moum, J. N. & Nash, J. D. 2011 Narrowband oscillations in the upper equatorial ocean. Part II: properties of shear instabilities. J. Phys. Oceanogr. 41, 412–428.CrossRefGoogle Scholar
Strang, E. J. & Fernando, H. J. S. 2001 Entrainment and mixing in stratified shear flows. J. Fluid Mech. 428, 349–386.Google Scholar
Taylor, J. R.2008 Numerical simulations of the stratified oceanic bottom boundary layer. PhD thesis, University of California, San Diego.Google Scholar
Taylor, J. R. & Zhou, Q.2017 A multi-parameter criterion for layer formation in a stratified shear flow using buoyancy coordinates. J. Fluid Mech. (in press).CrossRefGoogle Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.Google Scholar
Thorpe, S. A. 2016 Layers and internal waves in uniformly stratified fluids stirred by vertical grids. J. Fluid Mech. 793, 380–413.Google Scholar
Tseng, Y. & Ferziger, J. H. 2001 Mixing and available potential energy in stratified flows. Phys. Fluids 13, 1281–1293.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Venaille, A., Gostiaux, L. & Sommeria, J. 2017 A statistical mechanics approach of mixing in stratified fluids. J. Fluid Mech. 810, 554–583.Google Scholar
Venayagamoorthy, S. K. & Koseff, J. R. 2016 On the flux Richardson number in stably stratified turbulence. J. Fluid Mech. 798, R1.Google Scholar
Winters, K. B. & D’Asaro, E. A. 1996 Diascalar flux and the rate of fluid mixing. J. Fluid Mech. 317, 179–193.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Woods, A. W., Caulfield, C. P., Landel, J. R. & Kuesters, A. 2010 Non-invasive turbulent mixing across a density interface in a turbulent Taylor–Couette flow. J. Fluid Mech. 663, 347–357.Google Scholar
Zhou, Q., Taylor, J. R. & Caulfield, C. P. 2017 Self-similar mixing in stratified plane Couette flow for varying Prandtl number. J. Fluid Mech. 820, 86–120.CrossRefGoogle Scholar