Hostname: page-component-7bb8b95d7b-495rp Total loading time: 0 Render date: 2024-09-22T23:53:02.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple instability of layered stratified plane Couette flow

Published online by Cambridge University Press:  17 January 2017

T. S. Eaves Open the ORCID record for T. S. Eaves [Opens in a new window]  and
C. P. Caulfield
T. S. Eaves*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
C. P. Caulfield
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: tse23@math.ubc.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We present the linear stability properties and nonlinear evolution of two-dimensional plane Couette flow for a statically stable Boussinesq three-layer fluid of total depth 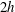$2h$ between two horizontal plates driven at constant velocity 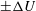$\pm \unicode[STIX]{x0394}U$. Initially the three layers have equal depth 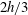$2h/3$ and densities 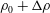$\unicode[STIX]{x1D70C}_{0}+\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$, 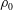$\unicode[STIX]{x1D70C}_{0}$ and 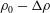$\unicode[STIX]{x1D70C}_{0}-\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$, such that 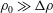$\unicode[STIX]{x1D70C}_{0}\gg \unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$. At finite Reynolds and Prandtl number, we demonstrate that this flow is susceptible to two distinct primary linear instabilities for sufficiently large bulk Richardson number 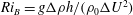$Ri_{B}=g\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}h/(\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x0394}U^{2})$. For a given bulk Richardson number 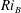$Ri_{B}$, the zero phase speed ‘Taylor’ instability is always predicted to have the largest growth rate and to be an inherently two-dimensional instability. An inherently viscous instability, reminiscent of the ‘Holmboe’ instability, is also predicted to have a non-zero growth rate. For flows with Prandtl number 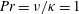$Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}=1$, where $\unicode[STIX]{x1D708}$ is the kinematic viscosity, and $\unicode[STIX]{x1D705}$ is the diffusivity of the density distribution, we find that the most unstable Taylor instability, maximized across wavenumber and 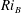$Ri_{B}$, has a (linear) growth rate which is a non-monotonic function of Reynolds number 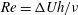$Re=\unicode[STIX]{x0394}Uh/\unicode[STIX]{x1D708}$, with a global maximum at 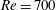$Re=700$ over 50 % larger than the growth rate as 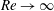$Re\rightarrow \infty$. In a fully nonlinear evolution of the flows with 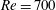$Re=700$ and 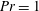$Pr=1$, the two interfaces between the three density layers diffuse more rapidly than the underlying instabilities can grow from small amplitude. Therefore, we investigate numerically the nonlinear evolution of the flow at 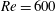$Re=600$ and 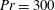$Pr=300$, and at 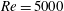$Re=5000$ and 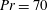$Pr=70$ in two-dimensional domains with streamwise extent equal to two wavelengths of the Taylor instability with the largest growth rate. At both sets of parameter values, the primary Taylor instability undergoes a period of identifiable exponential ‘linear’ growth. However, we demonstrate that, unlike the so-called ‘Kelvin–Helmholtz’ instability that it superficially resembles, the Taylor instability’s finite-amplitude state of an elliptical vortex in the middle layer appears not to saturate into a quasiequilibrium state, but is rapidly destroyed by the background shear. The decay process reveals 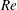$Re$-dependent secondary processes. For the 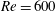$Re=600$ simulation, this decay allows the development to finite amplitude of the co-existing primary ‘viscous Holmboe wave instability’, which has a substantially smaller linear growth rate. For the 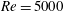$Re=5000$ simulation, the Taylor instability decay induces a non-trivial modification of the mean velocity and density distributions, which nonlinearly develops into more classical finite-amplitude Holmboe waves. In both cases, the saturated nonlinear Holmboe waves are robust and long-lived in two-dimensional flow.

JFM classification

Instability: Instability Instability: Nonlinear instability Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 813 , 25 February 2017 , pp. 250 - 278
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arratia, C., Caulfield, C. P. & Chomaz, J.-M. 2013 Transient perturbation growth in time-dependent mixing layers. J. Fluid Mech. 717, 90–133.Google Scholar
Balmforth, N. J., Roy, A. & Caulfield, C. P. 2012 Dynamics of vorticity defects in stratified shear flow. J. Fluid Mech. 694, 292–331.CrossRefGoogle Scholar
Bretherton, F. P. 1966 Critical layer instability in baroclinic flows. Q. J. R. Meteorol. Soc. 92, 325–334.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Cairns, R. A. 1979 The role of negative energy waves in some instabilities of parallel flows. J. Fluid Mech. 92, 1–14.Google Scholar
Carpenter, J. R., Balmforth, N. J. & Lawrence, G. A. 2010a Identifying unstable modes in stratified shear layers. Phys. Fluids 22, 054104.CrossRefGoogle Scholar
Carpenter, J. R., Tedford, E. W., Heifetz, E. & Lawrence, G. A. 2011 Instability in stratified shear flow: Review of a physical interpretation based on interacting waves. Appl. Mech. Rev. 64, 060801.Google Scholar
Carpenter, J. R., Tedford, E. W., Rahmani, M. & Lawrence, G. A. 2010b Holmboe wave fields in simulation and experiment. J. Fluid Mech. 648, 205–223.Google Scholar
Case, K. M. 1960 Stability of inviscid plane Couette flow. Phys. Fluids 3, 143–148.Google Scholar
Caulfield, C. P. 1994 Multiple linear instability of layered stratified shear flow. J. Fluid Mech. 258, 255–285.Google Scholar
Caulfield, C. P. & Peltier, W. R. 2000 The anatomy of the mixing transition in homogeneous and stratified free shear layers. J. Fluid Mech. 412, 1–47.Google Scholar
Caulfield, C. P., Peltier, W. R., Yoshida, S. & Ohtani, M. 1995 An experimental investigation of the instability of a shear flow with multilayered density stratification. Phys. Fluids 7, 3028–3041.Google Scholar
Churilov, S. M. 2016 Stability of shear flows with multilayered density stratification and monotonic velocity profiles having no inflection points. Geophys. Astrophys. Fluid Dyn. 110, 78–108.Google Scholar
Craik, A. D. 1988 Wave Interactions and Fluid Flows. Cambridge University Press.Google Scholar
Fjortoft, R. 1950 Application of integral theorems in deriving criteria of stability for laminar flows and for the baroclinic circular vortex. Geophys. Publ. 17, 1–52.Google Scholar
Goldstein, S. 1931 On the stability of superposed streams of fluids of different densities. Proc. R. Soc. Lond. 132, 524–548.Google Scholar
Guha, A. & Lawrence, G. A. 2014 A wave interaction approach to studying non-modal homogeneous and stratified shear instabilities. J. Fluid Mech. 755, 336–364.Google Scholar
van Haren, H., Gostiaux, L., Morozov, E. & Tarakanov, R. 2014 Extremely long Kelvin–Helmholtz billow trains in the Romanche fracture zone. Geophys. Res. Lett. 41, 8445–8451.Google Scholar
Haurwitz, B. 1931 Zur Theorie der Wellenbewegungen in Luft und Wasser (On the theory of wave motion in air and water). Geophysikalischen Institut der Universität Leipzig.Google Scholar
Hazel, P. 1972 Numerical studies of the stability of inviscid stratified shear flows. J. Fluid Mech. 51, 39–61.Google Scholar
Heifetz, E. & Mak, J. 2015 Stratified shear flow instabilities in the non-Boussinesq regime. Phys. Fluids 27, 086601.Google Scholar
Helmholtz, H. 1868 On discontinuous movements of fluids. Phil. Mag. 36, 337–346.CrossRefGoogle Scholar
Holmboe, J. 1962 On the behavior of symmetric waves in stratified shear layers. Geophys. Publ. 24, 67–113.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.Google Scholar
Huppert, H. E. 1973 On Howard’s technique for perturbing neutral solutions of the Taylor–Goldstein equation. J. Fluid Mech. 57, 361–368.Google Scholar
Lord Kelvin 1871 Hydrokinetic solutions and observations. Phil. Mag. 42, 362–377.Google Scholar
Lawrence, G. A., Browand, F. K. & Redekopp, L. G. 1991 The stability of a sheared density interface. Phys. Fluids A 3, 2360–2370.Google Scholar
Lee, V. & Caulfield, C. P. 2001 Nonlinear evolution of a layered stratified shear flow. Dyn. Atmos. Oceans 34, 103–124.Google Scholar
Lindzen, R. S. & Barker, R. S. 1985 Instability and wave over-reflection in stably stratified shear flow. J. Fluid Mech. 151, 189–217.Google Scholar
Lindzen, R. S. & Rambaldi, S. 1986 A study of over-reflection in viscous Poiseuille flow. J. Fluid Mech. 165, 355–372.Google Scholar
Mashayek, A., Caulfield, C. P. & Peltier, W. R. 2013 Time-dependent, non-monotonic mixing in stratified turbulent shear flows: implications for oceanographic estimates of buoyancy flux. J. Fluid Mech. 736, 570–593.Google Scholar
Mashayek, A. & Peltier, W. R. 2012a The ‘zoo’ of secondary instabilities precursory to stratified shear flow transition. Part 1. Shear aligned convection, pairing, and braid instabilities. J. Fluid Mech. 708, 5–44.Google Scholar
Mashayek, A. & Peltier, W. R. 2012b The ‘zoo’ of secondary instabilities precursory to stratified shear flow transition. Part 2. The influence of stratification. J. Fluid Mech. 708, 45–70.Google Scholar
Mashayek, A. & Peltier, W. R. 2013 Shear-induced mixing in geophysical flows: does the route to turbulence matter to its efficiency? J. Fluid Mech. 725, 216–261.Google Scholar
Meyer, C. R. & Linden, P. F. 2014 Stratified shear flow: experiments in an inclined duct. J. Fluid Mech. 753, 242–253.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.Google Scholar
Moser, R. D. & Rogers, M. M. 1991 Mixing transition and the cascade to small scales in a plane mixing layer. Phys. Fluids A 3, 1128–1134.Google Scholar
Oglethorpe, R. L. F., Caulfield, C. P. & Woods, A. W. 2013 Spontaneous layering in stratified turbulent Taylor–Couette flow. J. Fluid Mech. 721, R3.Google Scholar
Orr, W. M. F. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part I. A perfect liquid. Proc. R. Irish Acad. A 27, 9–68.Google Scholar
Phillips, O. M. 1972 Turbulence in a strongly stratified fluid – is it unstable? Deep-Sea Res. 19, 79–81.Google Scholar
Lord Rayleigh 1880 On the stability, or instability, of certain fluid motions. Proc. Lond. Math. Soc. 11, 57–72.Google Scholar
Romanov, V. A. 1973 Stability of plane-parallel Couette flow. Funct. Anal. Applics. 7, 137–146.Google Scholar
Rosenhead, L. 1931 The formation of vortices from a surface discontinuity. Proc. R. Soc. Lond. A 124, 170–192.Google Scholar
Salehipour, H., Caulfield, C. P. & Peltier, C. P. 2016 Turbulent mixing due to the Holmboe wave instability at high Reynolds number. J. Fluid Mech. 803, 591–621.Google Scholar
Scinocca, J. F. & Ford, R. 2000 The nonlinear forcing of large-scale internal gravity waves by a stratified shear instability. J. Atmos. Sci. 57, 653–672.Google Scholar
Smyth, W. D., Klaasen, G. P. & Peltier, W. R. 1988 Finite amplitude Holmboe waves. J. Geophys. Astrophys. Fluid Dyn. 43, 181–222.Google Scholar
Smyth, W. D., Moum, J. N. & Nash, J. D. 2011 Narrowband oscillations in the upper equatorial ocean. Part II. Properties of shear instabilities. J. Phys. Oceanogr. 41, 412–428.Google Scholar
Smyth, W. D. & Winters, K. B. 2003 Turbulence and mixing in Holmboe waves. J. Phys. Oceanogr. 33, 694–711.Google Scholar
Squire, H. B. 1933 On the stability of three-dimensional disturbances of viscous flow between parallel walls. Proc. R. Soc. Lond. A 142, 621–628.Google Scholar
Sutherland, B. R. 2010 Internal Gravity Waves. Cambridge University Press.Google Scholar
Taylor, G. I. 1931 Effect of variation in density on the stability of superposed streams of fluid. Proc. R. Soc. Lond. 132, 449–523.Google Scholar
Taylor, J. R.2008 Numerical simulations of the stratified oceanic bottom boundary layer. PhD thesis, Mech. Eng., UCSD.Google Scholar
Tedford, E. W., Pieters, R. & Lawrence, G. A. 2009 Symmetric Holmboe instabilities in a laboratory exchange flow. J. Fluid Mech. 636, 137–153.Google Scholar
Thorpe, S. A. 1968 A method of producing a shear flow in a stratified fluid. J. Fluid Mech. 32, 693–704.Google Scholar
Yih, C.-S. 1955 Stability of two-dimensional parallel flows for three-dimensional disturbances. Q. Appl. Maths 12, 434–435.Google Scholar
Zhu, D. Z. & Lawrence, G. A. 2001 Holmboe’s instability in exchange flows. J. Fluid Mech. 429, 391–409.Google Scholar

Eaves and Caulfield supplementary movie

Video of the time evolution of the perturbation vorticity and total density fields as described in the main text for the P600 simulation (Re = 600 and Pr = 300).

Download Eaves and Caulfield supplementary movie(Video)
Video 4.5 MB

Eaves and Caulfield supplementary movie

Video of the time evolution of the perturbation vorticity and total density fields as described in the main text for the S5000 simulation (Re = 5000 and Pr = 70).

Download Eaves and Caulfield supplementary movie(Video)
Video 6.4 MB