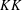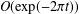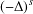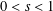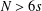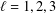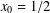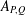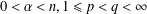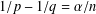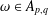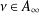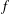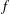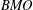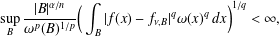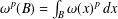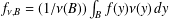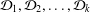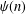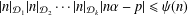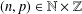Research Article
FACTORISATION OF EQUIVARIANT SPECTRAL TRIPLES IN UNBOUNDED
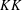 $KK$-THEORY
$KK$-THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2018, pp. 145-180
-
- Article
- Export citation
CHARACTERIZING HERMITIAN VARIETIES IN THREE- AND FOUR-DIMENSIONAL PROJECTIVE SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2018, pp. 1-8
-
- Article
-
- You have access
- Export citation
CHEBYSHEV SUBSETS OF A HILBERT SPACE SPHERE
- Part of:
-
- Published online by Cambridge University Press:
- 21 November 2019, pp. 289-301
-
- Article
- Export citation
AC-GORENSTEIN RINGS AND THEIR STABLE MODULE CATEGORIES
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2018, pp. 181-198
-
- Article
- Export citation
A MAGNETIC DOUBLE INTEGRAL
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2019, pp. 9-25
-
- Article
-
- You have access
- Open access
- Export citation
CHECKERBOARD COPULAS OF MAXIMUM ENTROPY WITH PRESCRIBED MIXED MOMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 26 November 2018, pp. 302-318
-
- Article
- Export citation
LOCALLY COMPACT WREATH PRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 15 August 2018, pp. 26-52
-
- Article
-
- You have access
- Export citation
SPECTRA OF LINEAR FRACTIONAL COMPOSITION OPERATORS ON THE GROWTH SPACE AND BLOCH SPACE OF THE UPPER HALF-PLANE
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2018, pp. 199-214
-
- Article
- Export citation
ON THE ACCURACY OF ASYMPTOTIC APPROXIMATIONS TO THE LOG-GAMMA AND RIEMANN–SIEGEL THETA FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2018, pp. 319-337
-
- Article
- Export citation
INFINITELY MANY SOLUTIONS FOR NONLOCAL SYSTEMS INVOLVING FRACTIONAL LAPLACIAN UNDER NONCOMPACT SETTINGS
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2018, pp. 215-233
-
- Article
- Export citation
ON SOME NEW MOCK THETA FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2018, pp. 53-66
-
- Article
-
- You have access
- Export citation
HYPERGEOMETRIC MODULAR EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 27 December 2018, pp. 338-366
-
- Article
-
- You have access
- Open access
- Export citation
CONTACT METRIC THREE-MANIFOLDS WITH CONSTANT SCALAR TORSION
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2018, pp. 234-255
-
- Article
- Export citation
RAMANUJAN SERIES WITH A SHIFT
- Part of:
-
- Published online by Cambridge University Press:
- 23 October 2018, pp. 367-380
-
- Article
- Export citation
CONTENT AND SINGLETONS BRING UNIQUE IDENTIFICATION MINORS
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2018, pp. 67-90
-
- Article
-
- You have access
- Export citation
CHARACTERIZATIONS OF BMO AND LIPSCHITZ SPACES IN TERMS OF
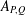 $A_{P,Q}$ WEIGHTS AND THEIR APPLICATIONS
$A_{P,Q}$ WEIGHTS AND THEIR APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2019, pp. 381-391
-
- Article
- Export citation
CLASSICAL PROPERTIES OF COMPOSITION OPERATORS ON HARDY–ORLICZ SPACES ON PLANAR DOMAINS
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2018, pp. 256-271
-
- Article
- Export citation
SOME REFINED RESULTS ON THE MIXED LITTLEWOOD CONJECTURE FOR PSEUDO-ABSOLUTE VALUES
- Part of:
-
- Published online by Cambridge University Press:
- 22 August 2018, pp. 91-109
-
- Article
-
- You have access
- Export citation
TAME DISCRETE SUBSETS IN STEIN MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 26 December 2018, pp. 110-132
-
- Article
-
- You have access
- Export citation
GENERALIZED CONTINUED FRACTION EXPANSIONS WITH CONSTANT PARTIAL DENOMINATORS
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2018, pp. 272-288
-
- Article
- Export citation