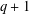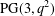Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Innamorati, Stefano
and
Zuanni, Fulvio
2020.
A combinatorial characterization of the Baer and the unital cone in $$PG(3,q^2)$$.
Journal of Geometry,
Vol. 111,
Issue. 3,
Aguglia, Angela
and
Pavese, Francesco
2020.
On non-singular Hermitian varieties of PG(4,q2).
Discrete Mathematics,
Vol. 343,
Issue. 1,
p.
111634.