Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-06-22T01:14:49.925Z Has data issue: false hasContentIssue false
  • English
  • Français

TAME DISCRETE SUBSETS IN STEIN MANIFOLDS

Part of: Complex spaces with a group of automorphisms Automorphic functions

Published online by Cambridge University Press:  26 December 2018

JÖRG WINKELMANN
JÖRG WINKELMANN*
Affiliation:
Lehrstuhl Analysis II, Mathematisches Institut, Ruhr-Universität Bochum, 44780 Bochum, Germany email joerg.winkelmann@rub.de
Get access Rights & Permissions [Opens in a new window]

Abstract

Rosay and Rudin introduced the notion of ‘tameness’ for discrete subsets of 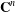$\mathbf{C}^{n}$. We generalize the notion of tameness for discrete sets to arbitrary Stein manifolds, with special emphasis on complex Lie groups.

Keywords

tame discrete setsemisimple complex Lie group

MSC classification

Primary: 32M10: Homogeneous complex manifolds
Secondary: 32M17: Automorphism groups of $^n$ and affine manifolds
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 1 , August 2019 , pp. 110 - 132
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrist, R. and Ugolini, R., Personal communication.Google Scholar
Buzzard, G. and Lu, S., ‘Algebraic surfaces holomorphically dominable by C 2 ’, Invent. Math. 139(3) (2000), 617–659.Google Scholar
Rosay, J. P. and Rudin, W., ‘Holomorphic maps from C n to C n ’, Trans. Amer. Math. Soc. 310 (1988), 47–86.Google Scholar
Winkelmann, J., ‘Large discrete sets in Stein manifolds’, Math. Z. 236 (2001), 883–901.Google Scholar
Winkelmann, J., ‘Tameness and growth conditions’, Doc. Math. 13 (2008), 97–101.Google Scholar