Article contents
CHARACTERIZATIONS OF BMO AND LIPSCHITZ SPACES IN TERMS OF 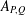 $A_{P,Q}$ WEIGHTS AND THEIR APPLICATIONS
$A_{P,Q}$ WEIGHTS AND THEIR APPLICATIONS
Published online by Cambridge University Press: 30 January 2019
Abstract
Let 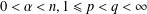 $0<\unicode[STIX]{x1D6FC}<n,1\leq p<q<\infty$ with
$0<\unicode[STIX]{x1D6FC}<n,1\leq p<q<\infty$ with 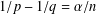 $1/p-1/q=\unicode[STIX]{x1D6FC}/n$,
$1/p-1/q=\unicode[STIX]{x1D6FC}/n$, 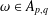 $\unicode[STIX]{x1D714}\in A_{p,q}$,
$\unicode[STIX]{x1D714}\in A_{p,q}$, 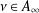 $\unicode[STIX]{x1D708}\in A_{\infty }$ and let
$\unicode[STIX]{x1D708}\in A_{\infty }$ and let 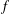 $f$ be a locally integrable function. In this paper, it is proved that
$f$ be a locally integrable function. In this paper, it is proved that 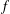 $f$ is in bounded mean oscillation
$f$ is in bounded mean oscillation 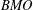 $\mathit{BMO}$ space if and only if
$\mathit{BMO}$ space if and only if 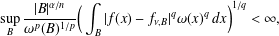 $$\begin{eqnarray}\sup _{B}\frac{|B|^{\unicode[STIX]{x1D6FC}/n}}{\unicode[STIX]{x1D714}^{p}(B)^{1/p}}\bigg(\int _{B}|f(x)-f_{\unicode[STIX]{x1D708},B}|^{q}\unicode[STIX]{x1D714}(x)^{q}\,dx\bigg)^{1/q}<\infty ,\end{eqnarray}$$
$$\begin{eqnarray}\sup _{B}\frac{|B|^{\unicode[STIX]{x1D6FC}/n}}{\unicode[STIX]{x1D714}^{p}(B)^{1/p}}\bigg(\int _{B}|f(x)-f_{\unicode[STIX]{x1D708},B}|^{q}\unicode[STIX]{x1D714}(x)^{q}\,dx\bigg)^{1/q}<\infty ,\end{eqnarray}$$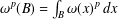 $\unicode[STIX]{x1D714}^{p}(B)=\int _{B}\unicode[STIX]{x1D714}(x)^{p}\,dx$ and
$\unicode[STIX]{x1D714}^{p}(B)=\int _{B}\unicode[STIX]{x1D714}(x)^{p}\,dx$ and 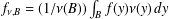 $f_{\unicode[STIX]{x1D708},B}=(1/\unicode[STIX]{x1D708}(B))\int _{B}f(y)\unicode[STIX]{x1D708}(y)\,dy$. We also show that
$f_{\unicode[STIX]{x1D708},B}=(1/\unicode[STIX]{x1D708}(B))\int _{B}f(y)\unicode[STIX]{x1D708}(y)\,dy$. We also show that 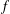 $f$ belongs to Lipschitz space
$f$ belongs to Lipschitz space 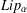 $Lip_{\unicode[STIX]{x1D6FC}}$ if and only if
$Lip_{\unicode[STIX]{x1D6FC}}$ if and only if 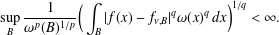 $$\begin{eqnarray}\sup _{B}\frac{1}{\unicode[STIX]{x1D714}^{p}(B)^{1/p}}\bigg(\int _{B}|f(x)-f_{\unicode[STIX]{x1D708},B}|^{q}\unicode[STIX]{x1D714}(x)^{q}\,dx\bigg)^{1/q}<\infty .\end{eqnarray}$$
$$\begin{eqnarray}\sup _{B}\frac{1}{\unicode[STIX]{x1D714}^{p}(B)^{1/p}}\bigg(\int _{B}|f(x)-f_{\unicode[STIX]{x1D708},B}|^{q}\unicode[STIX]{x1D714}(x)^{q}\,dx\bigg)^{1/q}<\infty .\end{eqnarray}$$
MSC classification
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 107 , Issue 3 , December 2019 , pp. 381 - 391
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
References
- 1
- Cited by




