Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-18T17:23:43.441Z Has data issue: false hasContentIssue false
  • English
  • Français

HYPERGEOMETRIC MODULAR EQUATIONS

Part of: Discontinuous groups and automorphic forms Sequences and sets Computational number theory

Published online by Cambridge University Press:  27 December 2018

SHAUN COOPER  and
WADIM ZUDILIN Open the ORCID record for WADIM ZUDILIN [Opens in a new window]
SHAUN COOPER
Affiliation:
Institute of Natural and Mathematical Sciences, Massey University – Albany, Private Bag 102904, North Shore Mail Centre, Auckland 0745, New Zealand email s.cooper@massey.ac.nz
WADIM ZUDILIN*
Affiliation:
Department of Mathematics, IMAPP, Radboud University, PO Box 9010, 6500 GL Nijmegen, Netherlands email w.zudilin@math.ru.nl School of Mathematical and Physical Sciences, The University of Newcastle, Callaghan, NSW 2308, Australia email wadim.zudilin@newcastle.edu.au
*
✉w.zudilin@math.ru.nl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We record 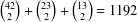$\binom{42}{2}+\binom{23}{2}+\binom{13}{2}=1192$ functional identities that, apart from being amazingly amusing in themselves, find application in the derivation of Ramanujan-type formulas for 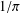$1/\unicode[STIX]{x1D70B}$ and in the computation of mathematical constants.

Keywords

Ramanujan-type formulahypergeometric modular equations

MSC classification

Primary: 33C20: Generalized hypergeometric series, $_pF_q$
Secondary: 11B65: Binomial coefficients; factorials; $q$-identities 11F11: Holomorphic modular forms of integral weight 11Y60: Evaluation of constants
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 3 , December 2019 , pp. 338 - 366
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© 2018 Australian Mathematical Publishing Association Inc.

References

Aldawoud, A. M., ‘Ramanujan-type series for $1/\unicode[STIX]{x1D70B}$ with quadratic irrationals’, Master of Science Thesis, Massey University, Auckland, 2012.Google Scholar
Almkvist, G., van Straten, D. and Zudilin, W., ‘Generalizations of Clausen’s formula and algebraic transformations of Calabi–Yau differential equations’, Proc. Edinb. Math. Soc. 54 (2011), 273–295.Google Scholar
Andrews, G. E., Askey, R. and Roy, R., Special Functions, Encyclopedia of Mathematics and its Applications, 71 (Cambridge University Press, Cambridge, 1999).Google Scholar
Aycock, A., ‘On proving some of Ramanujan’s formulas for $1/\unicode[STIX]{x1D70B}$ with an elementary method’, Preprint, 2013, arXiv:1309.1140v2 [math.NT].Google Scholar
Baruah, N. D. and Berndt, B. C., ‘Eisenstein series and Ramanujan-type series for 1/𝜋’, Ramanujan J. 23 (2010), 17–44.Google Scholar
Berndt, B. C., Bhargava, S. and Garvan, F. G., ‘Ramanujan’s theories of elliptic functions to alternative bases’, Trans. Amer. Math. Soc. 347 (1995), 4163–4244.Google Scholar
Borwein, J. M. and Borwein, P. B., Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity, Canadian Mathematical Society Series of Monographs and Advanced Texts (John Wiley, New York, 1987).Google Scholar
Chan, H. H., Chan, S. H. and Liu, Z.-G., ‘Domb’s numbers and Ramanujan–Sato type series for 1/𝜋’, Adv. Math. 186 (2004), 396–410.Google Scholar
Chan, H. H. and Cooper, S., ‘Rational analogues of Ramanujan’s series for 1/𝜋’, Math. Proc. Cambridge Philos. Soc. 153 (2012), 361–383.Google Scholar
Chan, H. H., Tanigawa, Y., Yang, Y. and Zudilin, W., ‘New analogues of Clausen’s identities arising from the theory of modular forms’, Adv. Math. 228 (2011), 1294–1314.Google Scholar
Chan, H. H. and Zudilin, W., ‘New representations for ApĂ©ry-like sequences’, Mathematika 56 (2010), 107–117.Google Scholar
Chudnovsky, D. V. and Chudnovsky, G. V., ‘Approximations and complex multiplication according to Ramanujan’, in: Ramanujan Revisited (Urbana-Champaign, IL, 1987) (Academic Press, Boston, MA, 1988), 375–472.Google Scholar
Cooper, S., ‘Inversion formulas for elliptic functions’, Proc. Lond. Math. Soc. 99 (2009), 461–483.Google Scholar
Cooper, S., ‘On Ramanujan’s function k (q) = r (q)r 2(q 2)’, Ramanujan J. 20 (2009), 311–328.Google Scholar
Cooper, S., ‘Level 10 analogues of Ramanujan’s series for 1/𝜋’, J. Ramanujan Math. Soc. 27 (2012), 59–76.Google Scholar
Cooper, S., Guillera, J., Straub, A. and Zudilin, W., ‘Crouching AGM, hidden modularity’, in: Frontiers in Orthogonal Polynomials and q-Series, Contemporary Mathematics and its Applications: Monographs, Expositions and Lecture Notes, 1 (eds. Zuhair Nashed, M. and Li, X.) (World Scientific, Singapore, 2018), 169–187.Google Scholar
Cooper, S. and Ye, D., ‘The level 12 analogue of Ramanujan’s function k ’, J. Aust. Math. Soc. 101 (2016), 29–53.Google Scholar
Goursat, É., ‘Sur l’équation diffĂ©rentielle linĂ©aire, qui admet pour intĂ©grale la sĂ©rie hypergĂ©omĂ©trique’, Ann. Sci. Éc. Norm. SupĂ©r. SĂ©r. 2 10 (1881), 3–142.Google Scholar
Guillera, J., ‘New proofs of Borwein-type algorithms for Pi’, Integral Transforms Spec. Funct. 27 (2016), 775–782.Google Scholar
Guillera, J. and Zudilin, W., ‘Ramanujan-type formulae for 1/𝜋: the art of translation’, in: The Legacy of Srinivasa Ramanujan, Ramanujan Mathematical Society Lecture Notes Series, 20 (eds. Berndt, B. C. and Prasad, D.) (Ramanujan Mathematical Society, Mysore, 2013), 181–195.Google Scholar
Maier, R. S., ‘Algebraic hypergeometric transformations of modular origin’, Trans. Amer. Math. Soc. 359 (2007), 3859–3885.Google Scholar
Ramanujan, S., Notebooks, Vol. 2 (Tata Institute of Fundamental Research, Bombay, 1957).Google Scholar
Ramanujan, S., ‘Modular equations and approximations to 𝜋’, Q. J. Math. 45 (1914), 350–372; reprinted in Collected Papers, 3rd printing (American Mathematical Society/Chelsea, Providence, RI, 2000), 23–39.Google Scholar
Rogers, M., ‘New 5 F 4 hypergeometric transformations, three-variable Mahler measures, and formulas for 1/𝜋’, Ramanujan J. 18 (2009), 327–340.Google Scholar
VidĆ«nas, R., ‘Algebraic transformations of Gauss hypergeometric functions’, Funkcial. Ekvac. 52 (2009), 139–180.Google Scholar
Zagier, D., ‘Integral solutions of ApĂ©ry-like recurrence equations’, in: Groups and Symmetries, CRM Proceedings and Lecture Notes, 47 (American Mathematical Society, Providence, RI, 2009), 349–366.Google Scholar
Zudilin, W., ‘Ramanujan-type formulae for 1/𝜋: a second wind?’, in: Modular Forms and String Duality (Banff, 3–8 June 2006), Fields Institute Communications, 54 (eds. Yui, N., Verrill, H. and Doran, C. F.) (American Mathematical Society, Providence, RI, 2008), 179–188.Google Scholar
Zudilin, W., ‘Lost in translation’, in: Advances in Combinatorics, Waterloo Workshop in Computer Algebra, W80 (Waterloo, 26–29 May 2011) (eds. Kotsireas, I. and Zima, E. V.) (Springer, New York, 2013), 287–293.Google Scholar