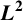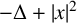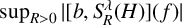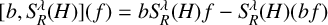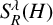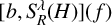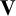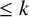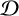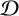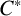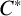Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
QUALITATIVE UNCERTAINTY PRINCIPLE ON CERTAIN LIE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2023, pp. 289-307
-
- Article
- Export citation
A WEIGHTED
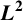 $\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
$\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
- Part of:
-
- Published online by Cambridge University Press:
- 15 January 2024, pp. 308-330
-
- Article
- Export citation
NORMAL SUBMONOIDS AND CONGRUENCES ON A MONOID
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2023, pp. 331-362
-
- Article
- Export citation
THE PRO-
 $\boldsymbol {k}$-SOLVABLE TOPOLOGY ON A FREE GROUP
$\boldsymbol {k}$-SOLVABLE TOPOLOGY ON A FREE GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 22 December 2023, pp. 363-383
-
- Article
- Export citation
FINITELY PRESENTED INVERSE SEMIGROUPS WITH FINITELY MANY IDEMPOTENTS IN EACH
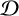 $\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS
$\mathcal D$-CLASS AND NON-HAUSDORFF UNIVERSAL GROUPOIDS
- Part of:
-
- Published online by Cambridge University Press:
- 13 December 2023, pp. 384-398
-
- Article
- Export citation
INDEX
-
- Published online by Cambridge University Press:
- 13 May 2024, p. 399
-
- Article
- Export citation
JAZ volume 116 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 13 May 2024, pp. f1-f2
-
- Article
-
- You have access
- Export citation
JAZ volume 116 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 13 May 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation