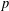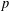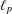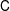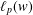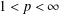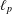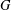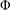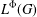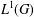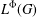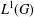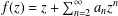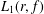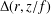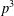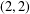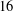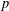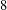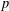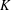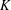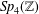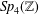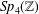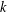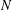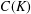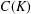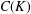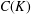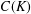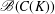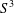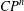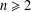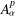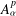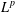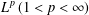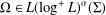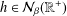Research Article
SEPARATION OF CONVEX SETS IN EXTENDED NORMED SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2015, pp. 145-165
-
- Article
-
- You have access
- Export citation
SPECTRUM AND COMPACTNESS OF THE CESÀRO OPERATOR ON WEIGHTED
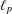 $\ell _{p}$ SPACES
$\ell _{p}$ SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 19 August 2015, pp. 287-314
-
- Article
-
- You have access
- Export citation
A CONVOLUTION-INDUCED TOPOLOGY ON THE ORLICZ SPACE OF A LOCALLY COMPACT GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 19 January 2015, pp. 1-11
-
- Article
-
- You have access
- Export citation
INTEGRAL MEANS AND DIRICHLET INTEGRAL FOR CERTAIN CLASSES OF ANALYTIC FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 16 July 2015, pp. 315-333
-
- Article
-
- You have access
- Export citation
THE CLASS OF (2, 2)-GROUPS WITH HOMOCYCLIC REGULATOR QUOTIENT OF EXPONENT
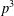 $p^{3}$ HAS BOUNDED REPRESENTATION TYPE
$p^{3}$ HAS BOUNDED REPRESENTATION TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2014, pp. 12-29
-
- Article
-
- You have access
- Export citation
ON COSINE FAMILIES CLOSE TO SCALAR COSINE FAMILIES
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2015, pp. 166-174
-
- Article
-
- You have access
- Export citation
BOUNDED MULTIPLE SOLUTIONS FOR
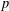 $p$-LAPLACIAN PROBLEMS WITH ARBITRARY PERTURBATIONS
$p$-LAPLACIAN PROBLEMS WITH ARBITRARY PERTURBATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2015, pp. 175-185
-
- Article
-
- You have access
- Export citation
ON DIFFERENTIAL CHARACTERISTIC CLASSES
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2014, pp. 30-47
-
- Article
-
- You have access
- Export citation
ON POWER MOMENTS OF THE HECKE MULTIPLICATIVE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 25 March 2015, pp. 334-340
-
- Article
-
- You have access
- Export citation
ON ISOMORPHISMS OF VERTEX-TRANSITIVE CUBIC GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 13 August 2015, pp. 341-349
-
- Article
-
- You have access
- Export citation
ON THE RESOLVENT OF THE LAPLACE–BELTRAMI OPERATOR IN HYPERBOLIC SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2015, pp. 186-206
-
- Article
-
- You have access
- Export citation
SOME MONODROMY GROUPS OF FINITE INDEX IN
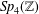 $\mathit{Sp}_{4}(\mathbb{Z})$
$\mathit{Sp}_{4}(\mathbb{Z})$
- Part of:
-
- Published online by Cambridge University Press:
- 30 March 2015, pp. 48-62
-
- Article
-
- You have access
- Export citation
AVERAGES OF TWISTED
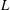 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 24 June 2015, pp. 207-236
-
- Article
-
- You have access
- Export citation
CHAINS OF FUNCTIONS IN
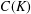 $C(K)$-SPACES
$C(K)$-SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 02 September 2015, pp. 350-363
-
- Article
-
- You have access
- Export citation
THE MINIMAL
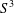 $S^{3}$ WITH CONSTANT SECTIONAL CURVATURE IN
$S^{3}$ WITH CONSTANT SECTIONAL CURVATURE IN 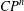 $\mathit{CP}^{n}$
$\mathit{CP}^{n}$
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2015, pp. 63-75
-
- Article
-
- You have access
- Export citation
ONE-POINT CONNECTIFICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2015, pp. 76-84
-
- Article
-
- You have access
- Export citation
A NEURAL NETWORK FOR THE GENERALIZED NONLINEAR COMPLEMENTARITY PROBLEM OVER A POLYHEDRAL CONE
-
- Published online by Cambridge University Press:
- 30 October 2015, pp. 364-379
-
- Article
-
- You have access
- Export citation
BOUNDED TOEPLITZ AND HANKEL PRODUCTS ON THE WEIGHTED BERGMAN SPACES OF THE UNIT BALL
- Part of:
-
- Published online by Cambridge University Press:
- 05 June 2015, pp. 237-249
-
- Article
-
- You have access
- Export citation
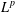 $L^{p}$ BOUNDS FOR NONISOTROPIC MARCINKIEWICZ INTEGRALS ASSOCIATED TO SURFACES
$L^{p}$ BOUNDS FOR NONISOTROPIC MARCINKIEWICZ INTEGRALS ASSOCIATED TO SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2015, pp. 380-398
-
- Article
-
- You have access
- Export citation
COEXISTENCE OF COILED SURFACES AND SPANNING SURFACES FOR KNOTS AND LINKS
- Part of:
-
- Published online by Cambridge University Press:
- 16 July 2015, pp. 250-259
-
- Article
-
- You have access
- Export citation