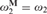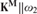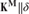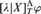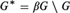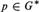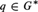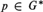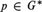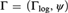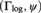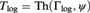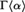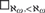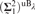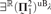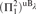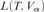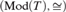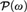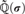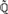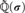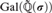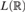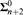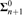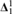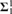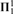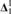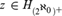Articles
A SYNTACTIC CHARACTERIZATION OF MORITA EQUIVALENCE
-
- Published online by Cambridge University Press:
- 09 January 2018, pp. 1181-1198
-
- Article
- Export citation
DOWNWARD TRANSFERENCE OF MICE AND UNIVERSALITY OF LOCAL CORE MODELS
-
- Published online by Cambridge University Press:
- 19 June 2017, pp. 385-419
-
- Article
- Export citation
PREDICATIVITY THROUGH TRANSFINITE REFLECTION
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 787-808
-
- Article
- Export citation
TURING DEGREE SPECTRA OF DIFFERENTIALLY CLOSED FIELDS
-
- Published online by Cambridge University Press:
- 21 March 2017, pp. 1-25
-
- Article
- Export citation
SQUARE WITH BUILT-IN DIAMOND-PLUS
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 809-833
-
- Article
- Export citation
LEFT MAXIMAL AND STRONGLY RIGHT MAXIMAL IDEMPOTENTS IN G*
-
- Published online by Cambridge University Press:
- 21 March 2017, pp. 26-34
-
- Article
- Export citation
MEASURING DEPENDENCE IN METRIC ABSTRACT ELEMENTARY CLASSES WITH PERTURBATIONS
-
- Published online by Cambridge University Press:
- 09 January 2018, pp. 1199-1228
-
- Article
- Export citation
OBLIGATION BLACKWELL GAMES AND P-AUTOMATA
-
- Published online by Cambridge University Press:
- 19 June 2017, pp. 420-452
-
- Article
- Export citation
NIP FOR THE ASYMPTOTIC COUPLE OF THE FIELD OF LOGARITHMIC TRANSSERIES
-
- Published online by Cambridge University Press:
- 21 March 2017, pp. 35-61
-
- Article
- Export citation
SQUARES AND NARROW SYSTEMS
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 834-859
-
- Article
- Export citation
UNIVERSALLY BAIRE SETS AND GENERIC ABSOLUTENESS
-
- Published online by Cambridge University Press:
- 09 January 2018, pp. 1229-1251
-
- Article
- Export citation
THE BOREL COMPLEXITY OF ISOMORPHISM FOR O-MINIMAL THEORIES
-
- Published online by Cambridge University Press:
- 19 June 2017, pp. 453-473
-
- Article
- Export citation
A MODEL-THEORETIC CHARACTERIZATION OF MONADIC SECOND ORDER LOGIC ON INFINITE WORDS
-
- Published online by Cambridge University Press:
- 21 March 2017, pp. 62-76
-
- Article
- Export citation
DEFINABILITY OF DERIVATIONS IN THE REDUCTS OF DIFFERENTIALLY CLOSED FIELDS
-
- Published online by Cambridge University Press:
- 09 January 2018, pp. 1252-1277
-
- Article
- Export citation
GENERIC LARGE CARDINALS AND SYSTEMS OF FILTERS
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 860-892
-
- Article
- Export citation
DECIDABLE ALGEBRAIC FIELDS
-
- Published online by Cambridge University Press:
- 19 June 2017, pp. 474-488
-
- Article
- Export citation
CANONICAL MODELS FOR FRAGMENTS OF THE AXIOM OF CHOICE
-
- Published online by Cambridge University Press:
- 19 June 2017, pp. 489-509
-
- Article
- Export citation
ON THE UNIFORM COMPUTATIONAL CONTENT OF RAMSEY’S THEOREM
-
- Published online by Cambridge University Press:
- 09 January 2018, pp. 1278-1316
-
- Article
- Export citation
EQUIVALENCE RELATIONS WHICH ARE BOREL SOMEWHERE
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 893-930
-
- Article
- Export citation
COMPUTABLE FUNCTORS AND EFFECTIVE INTERPRETABILITY
-
- Published online by Cambridge University Press:
- 25 January 2017, pp. 77-97
-
- Article
- Export citation