Article contents
EQUIVALENCE RELATIONS WHICH ARE BOREL SOMEWHERE
Published online by Cambridge University Press: 08 September 2017
Abstract
The following will be shown: Let I be a σ-ideal on a Polish space X so that the associated forcing of I+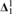 ${\bf{\Delta }}_1^1$ sets ordered by ⊆ is a proper forcing. Let E be a
${\bf{\Delta }}_1^1$ sets ordered by ⊆ is a proper forcing. Let E be a 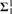 ${\bf{\Sigma }}_1^1$ or a
${\bf{\Sigma }}_1^1$ or a 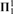 ${\bf{\Pi }}_1^1$ equivalence relation on X with all equivalence classes
${\bf{\Pi }}_1^1$ equivalence relation on X with all equivalence classes 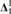 ${\bf{\Delta }}_1^1$. If for all
${\bf{\Delta }}_1^1$. If for all 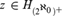 $z \in {H_{{{\left( {{2^{{\aleph _0}}}} \right)}^ + }}}$, z♯ exists, then there exists an I+
$z \in {H_{{{\left( {{2^{{\aleph _0}}}} \right)}^ + }}}$, z♯ exists, then there exists an I+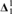 ${\bf{\Delta }}_1^1$ set C ⊆ X such that E ↾ C is a
${\bf{\Delta }}_1^1$ set C ⊆ X such that E ↾ C is a 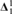 ${\bf{\Delta }}_1^1$ equivalence relation.
${\bf{\Delta }}_1^1$ equivalence relation.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
- 1
- Cited by




