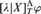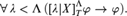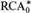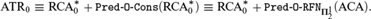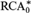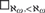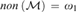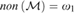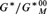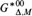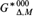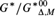Articles
PREDICATIVITY THROUGH TRANSFINITE REFLECTION
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 787-808
-
- Article
- Export citation
SQUARE WITH BUILT-IN DIAMOND-PLUS
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 809-833
-
- Article
- Export citation
SQUARES AND NARROW SYSTEMS
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 834-859
-
- Article
- Export citation
GENERIC LARGE CARDINALS AND SYSTEMS OF FILTERS
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 860-892
-
- Article
- Export citation
EQUIVALENCE RELATIONS WHICH ARE BOREL SOMEWHERE
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 893-930
-
- Article
- Export citation
DENSITY-1-BOUNDING AND QUASIMINIMALITY IN THE GENERIC DEGREES
-
- Published online by Cambridge University Press:
- 08 May 2017, pp. 931-957
-
- Article
- Export citation
THE ONTO MAPPING OF SIERPINSKI AND NONMEAGER SETS
-
- Published online by Cambridge University Press:
- 16 May 2017, pp. 958-965
-
- Article
- Export citation
ON TARSKI’S AXIOMATIC FOUNDATIONS OF THE CALCULUS OF RELATIONS
-
- Published online by Cambridge University Press:
- 08 May 2017, pp. 966-994
-
- Article
- Export citation
TAMENESS AND FRAMES REVISITED
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 995-1021
-
- Article
- Export citation
METRIC ABSTRACT ELEMENTARY CLASSES AS ACCESSIBLE CATEGORIES
-
- Published online by Cambridge University Press:
- 08 May 2017, pp. 1022-1040
-
- Article
- Export citation
DECIDABILITY AND CLASSIFICATION OF THE THEORY OF INTEGERS WITH PRIMES
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 1041-1050
-
- Article
- Export citation
UNIMODULARITY UNIFIED
-
- Published online by Cambridge University Press:
- 08 May 2017, pp. 1051-1065
-
- Article
- Export citation
RETRACTED – MEASURING CLUB-SEQUENCES TOGETHER WITH THE CONTINUUM LARGE
- Part of:
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 1066-1079
-
- Article
- Export citation
DEFINABLE TOPOLOGICAL DYNAMICS
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 1080-1105
-
- Article
- Export citation
Σ1(κ)-DEFINABLE SUBSETS OF H(κ+)
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 1106-1131
-
- Article
- Export citation
GEOMETRIC REPRESENTATION IN THE THEORY OF PSEUDO-FINITE FIELDS
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1132-1139
-
- Article
- Export citation
THE DIOPHANTINE PROBLEM FOR ADDITION AND DIVISIBILITY OVER SUBRINGS OF THE RATIONALS
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 1140-1149
-
- Article
- Export citation
AUTOMORPHISM GROUPS OF RANDOMIZED STRUCTURES
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. 1150-1179
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JSL volume 82 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JSL volume 82 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 08 September 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation