Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-23T23:27:35.672Z Has data issue: false hasContentIssue false
  • English
  • Français

DEFINABILITY OF DERIVATIONS IN THE REDUCTS OF DIFFERENTIALLY CLOSED FIELDS

Published online by Cambridge University Press:  09 January 2018

VAHAGN ASLANYAN
VAHAGN ASLANYAN*
Affiliation:
MATHEMATICAL INSTITUTE UNIVERSITY OF OXFORD OXFORD OX2 6GG, UKE-mail: vahagn.aslanyan@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 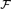${\cal F}$ =(F; +, .,0, 1, D) be a differentially closed field. We consider the question of definability of the derivation D in reducts of 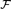${\cal F}$ of the form 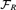${\cal F}$R = (F; +, .,0, 1, P)P ε R where R is some collection of definable sets in 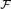${\cal F}$. We give examples and nonexamples and establish some criteria for definability of D. Finally, using the tools developed in the article, we prove that under the assumption of inductiveness of Th (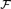${\cal F}$R) model completeness is a necessary condition for definability of D. This can be seen as part of a broader project where one is interested in finding Ax-Schanuel type inequalities (or predimension inequalities) for differential equations.

Keywords

03C1003C6012H0512H2013N15model theoretic algebradifferentially closed fieldreductabstract differential equationdefinable derivation
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 4 , December 2017 , pp. 1252 - 1277
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aslanyan, V., Ax-Schanuel type inequalities in differentially closed fields. Ph.D. thesis, University of Oxford, 2017. Available at https://ora.ox.ac.uk/objects/uuid:bced8c2d-22df-4a21-9a1f-5e4204b6c85d.Google Scholar
Ax, J., On Schanuel’s conjectures. Annals of Mathematics, vol. 93 (1971), pp. 252–268.Google Scholar
Hasson, A. and Sustretov, D., Incidence systems on Cartesian powers of algebraic curves, preprint, 2017. arXiv:1702.05554 [math.LO].Google Scholar
Hrushovski, E., A new strongly minimal set. Annals of Pure and Applied Logic, vol. 62 (1993), no. 2, pp. 147–166.Google Scholar
Kaplansky, I., An Introduction to Differential Algebra, Publications de l’institut de mathematique de l’universite de Nancago, Paris, 1957.Google Scholar
Kirby, J., The theory of the exponential differential equations of semiableian verieties. Selecta Mathematics, vol. 15 (2009), no. 3, pp. 445–486.Google Scholar
Marker, D., Model Theory: An Introduction, Springer, New York, 2002.Google Scholar
Marker, D., Model theory of differential fields, Model Theory of Fields (Marker, D., Messmer, M., and Pillay, A., editors), Lecture Notes in Logic, vol. 5, Springer-Verlag, Berlin, 2005.Google Scholar
Pillay, A., Differential fields, Lectures on Algebraic Model Theory (Hart, B. and Valeriote, M., editors), Fields Institute Monographs, Providence, RI, 2001.Google Scholar
Pillay, A., Applied Stability Theory, Lecture Notes, 2003.Google Scholar
Poizat, B., A Course in Model Theory, Springer, New York, 2000.CrossRefGoogle Scholar
Pila, J. and Tsimerman, J., Ax-Schanuel for the j-function. Duke Mathematical Journal, vol. 165 (2016), no. 13, pp. 2587–2605.Google Scholar
Rabinovich, E., Definability of a Field in Sufficiently Rich Incidence Systems, QMW Maths Notes, vol. 14, Queen Mary and Westfield College, London, 1993.Google Scholar
Suer, S., Model theory of differentially closed fields with several commuting derivations. Ph.D. thesis, University of Illinois, Urbana Champaign, 2007.Google Scholar
Tent, K. and Ziegler, M., A Course in Model Theory, Cambridge University Press, Cambridge, 2012.Google Scholar
Wagner, F. O., Relational structures and dimensions, Automorphisms of First-Order Structures, OUP (Kaye, R. and Macpherson, D., editors), Oxford University Press, Oxford, 1994, pp. 153–180.Google Scholar
Zilber, B., Exponential sums equations and the Schanuel conjecture. Journal of the London Mathematical Society, vol. 65 (2002), no. 2, pp. 27–44.Google Scholar
Zilber, B., Pseudo-exponentiation on algebraically closed fields of characteristic zero. Annals of Pure and Applied Logic, vol. 132 (2004), no. 1, pp. 67–95.Google Scholar
Zilber, B., Analytic and pseudo-analytic structures, Logic Colloquium 2000 (Cori, R., Razborov, A., Tudorcevic, S., and Wood, C., editors), Lecture Notes in Logic, vol. 19, Association for Symbolic Logic, Urbana, IL, 2005, pp. 392–408.Google Scholar
Zilber, B., Zariski Geometries, Cambridge University Press, Cambridge, 2009.Google Scholar
Zilber, B., Model theory of special subvarieties and Schanuel-type conjectures. Annals of Pure and Applied Logic, vol. 167 (2016), pp. 1000–1028.Google Scholar