No CrossRef data available.
Article contents
LEFT MAXIMAL AND STRONGLY RIGHT MAXIMAL IDEMPOTENTS IN G*
Published online by Cambridge University Press: 21 March 2017
Abstract
Let G be a countably infinite discrete group, let
βG be the Stone–Čech
compactification of G, and let 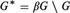 ${G^{\rm{*}}} = \beta G \setminus G$. An idempotent
${G^{\rm{*}}} = \beta G \setminus G$. An idempotent 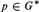 $p \in {G^{\rm{*}}}$ is left (right) maximal if for every idempotent
$p \in {G^{\rm{*}}}$ is left (right) maximal if for every idempotent 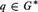 $q \in {G^{\rm{*}}}$, pq = p
(qp = P) implies qp
= q (qp =
q). An idempotent
$q \in {G^{\rm{*}}}$, pq = p
(qp = P) implies qp
= q (qp =
q). An idempotent  $p \in {G^{\rm{*}}}$ is strongly right maximal if the equation xp
= p has the unique solution x
= p in G*. We show that
there is an idempotent
$p \in {G^{\rm{*}}}$ is strongly right maximal if the equation xp
= p has the unique solution x
= p in G*. We show that
there is an idempotent  $p \in {G^{\rm{*}}}$ which is both left maximal and strongly right maximal.
$p \in {G^{\rm{*}}}$ which is both left maximal and strongly right maximal.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017


