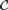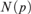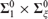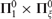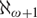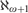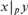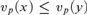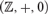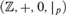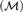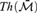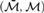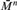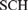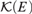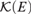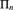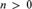Articles
A CORRECT POLYNOMIAL TRANSLATION OF S4 INTO INTUITIONISTIC LOGIC
-
- Published online by Cambridge University Press:
- 11 June 2019, pp. 439-451
-
- Article
- Export citation
EXISTENCE OF MODELING LIMITS FOR SEQUENCES OF SPARSE STRUCTURES
-
- Published online by Cambridge University Press:
- 07 March 2019, pp. 452-472
-
- Article
- Export citation
A TAIL CONE VERSION OF THE HALPERN–LÄUCHLI THEOREM AT A LARGE CARDINAL
-
- Published online by Cambridge University Press:
- 08 April 2019, pp. 473-496
-
- Article
- Export citation
BEING LOW ALONG A SEQUENCE AND ELSEWHERE
-
- Published online by Cambridge University Press:
- 25 January 2019, pp. 497-516
-
- Article
- Export citation
A SEPARATION RESULT FOR COUNTABLE UNIONS OF BOREL RECTANGLES
-
- Published online by Cambridge University Press:
- 22 February 2019, pp. 517-532
-
- Article
- Export citation
KRIPKE COMPLETENESS OF STRICTLY POSITIVE MODAL LOGICS OVER MEET-SEMILATTICES WITH OPERATORS
-
- Published online by Cambridge University Press:
- 03 April 2019, pp. 533-588
-
- Article
- Export citation
MINIMUM MODELS OF SECOND-ORDER SET THEORIES
-
- Published online by Cambridge University Press:
- 08 April 2019, pp. 589-620
-
- Article
- Export citation
DESTRUCTIBILITY OF THE TREE PROPERTY AT
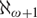 ${\aleph _{\omega + 1}}$
${\aleph _{\omega + 1}}$
-
- Published online by Cambridge University Press:
- 06 March 2019, pp. 621-631
-
- Article
- Export citation
A NEW DP-MINIMAL EXPANSION OF THE INTEGERS
-
- Published online by Cambridge University Press:
- 04 March 2019, pp. 632-663
-
- Article
- Export citation
A THEORY OF PAIRS FOR NON-VALUATIONAL STRUCTURES
-
- Published online by Cambridge University Press:
- 25 January 2019, pp. 664-683
-
- Article
- Export citation
THE HARRINGTON–SHELAH MODEL WITH LARGE CONTINUUM
-
- Published online by Cambridge University Press:
- 22 February 2019, pp. 684-703
-
- Article
- Export citation
DEFINABLY SIMPLE STABLE GROUPS WITH FINITARY GROUPS OF AUTOMORPHISMS
-
- Published online by Cambridge University Press:
- 10 April 2019, pp. 704-712
-
- Article
- Export citation
ITP, ISP, AND SCH
-
- Published online by Cambridge University Press:
- 08 February 2019, pp. 713-725
-
- Article
- Export citation
ON A METRIC GENERALIZATION OF THE tt-DEGREES AND EFFECTIVE DIMENSION THEORY
-
- Published online by Cambridge University Press:
- 12 March 2019, pp. 726-749
-
- Article
- Export citation
INDEPENDENCE IN GENERIC INCIDENCE STRUCTURES
-
- Published online by Cambridge University Press:
- 15 February 2019, pp. 750-780
-
- Article
- Export citation
Gδ Sets IN σ-IDEALS GENERATED BY COMPACT SETS
-
- Published online by Cambridge University Press:
- 04 March 2019, pp. 781-797
-
- Article
- Export citation
ALGEBRAIC NEW FOUNDATIONS
-
- Published online by Cambridge University Press:
- 05 February 2019, pp. 798-832
-
- Article
- Export citation
SPACES OF TYPES IN POSITIVE MODEL THEORY
-
- Published online by Cambridge University Press:
- 24 January 2019, pp. 833-848
-
- Article
- Export citation
AXIOMATIZATION OF PROVABLE n-PROVABILITY
-
- Published online by Cambridge University Press:
- 08 February 2019, pp. 849-869
-
- Article
- Export citation
MARKOV’S PRINCIPLE AND SUBSYSTEMS OF INTUITIONISTIC ANALYSIS
-
- Published online by Cambridge University Press:
- 26 February 2019, pp. 870-876
-
- Article
- Export citation