No CrossRef data available.
Article contents
Gδ Sets IN σ-IDEALS GENERATED BY COMPACT SETS
Published online by Cambridge University Press: 04 March 2019
Abstract
Given a compact Polish space E and the hyperspace of its compact subsets 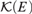 ${\cal K}\left( E \right)$, we consider Gδσ-ideals of compact subsets of E. Solecki has shown that any σ-ideal in a broad natural class of Gδ ideals can be represented via a compact subset of
${\cal K}\left( E \right)$, we consider Gδσ-ideals of compact subsets of E. Solecki has shown that any σ-ideal in a broad natural class of Gδ ideals can be represented via a compact subset of 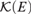 ${\cal K}\left( E \right)$; in this article we examine the behaviour of Gδ subsets of E with respect to the representing set. Given an ideal I in this class, we construct a representing set that recognises a compact subset of E as being “small” precisely when it is in I, and recognises a Gδ subset of E as being “small” precisely when it is covered by countably many compact sets from I.
${\cal K}\left( E \right)$; in this article we examine the behaviour of Gδ subsets of E with respect to the representing set. Given an ideal I in this class, we construct a representing set that recognises a compact subset of E as being “small” precisely when it is in I, and recognises a Gδ subset of E as being “small” precisely when it is covered by countably many compact sets from I.
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019


