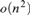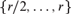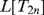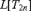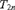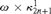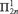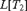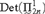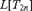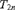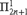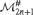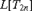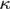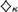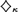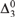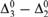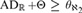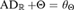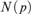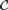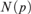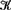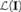Articles
DISCRETE METRIC SPACES: STRUCTURE, ENUMERATION, AND 0-1 LAWS
-
- Published online by Cambridge University Press:
- 19 August 2019, pp. 1293-1325
-
- Article
- Export citation
AN ANALYSIS OF THE MODELS
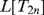 $L[T_{2n} ]$
$L[T_{2n} ]$
-
- Published online by Cambridge University Press:
- 04 February 2019, pp. 1-26
-
- Article
- Export citation
A CORRECT POLYNOMIAL TRANSLATION OF S4 INTO INTUITIONISTIC LOGIC
-
- Published online by Cambridge University Press:
- 11 June 2019, pp. 439-451
-
- Article
- Export citation
UNCOUNTABLE TREES AND COHEN
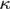 $\kappa$-REALS
$\kappa$-REALS
-
- Published online by Cambridge University Press:
- 02 July 2019, pp. 877-894
-
- Article
- Export citation
JOINT DIAMONDS AND LAVER DIAMONDS
-
- Published online by Cambridge University Press:
- 13 June 2019, pp. 895-928
-
- Article
- Export citation
A WEAKLY 2-GENERIC WHICH BOUNDS A MINIMAL DEGREE
-
- Published online by Cambridge University Press:
- 04 November 2019, pp. 1326-1347
-
- Article
- Export citation
DERIVED MODELS OF MICE BELOW THE LEAST FIXPOINT OF THE SOLOVAY SEQUENCE
-
- Published online by Cambridge University Press:
- 07 February 2019, pp. 27-53
-
- Article
- Export citation
EXISTENCE OF MODELING LIMITS FOR SEQUENCES OF SPARSE STRUCTURES
-
- Published online by Cambridge University Press:
- 07 March 2019, pp. 452-472
-
- Article
- Export citation
CONSTRUCTIVE REFLECTIVITY PRINCIPLES FOR REGULAR THEORIES
-
- Published online by Cambridge University Press:
- 30 September 2019, pp. 1348-1367
-
- Article
- Export citation
WEAK SATURATION AND WEAK AMALGAMATION PROPERTY
-
- Published online by Cambridge University Press:
- 04 July 2019, pp. 929-936
-
- Article
- Export citation
RANK LOGIC IS DEAD, LONG LIVE RANK LOGIC!
-
- Published online by Cambridge University Press:
- 14 March 2019, pp. 54-87
-
- Article
- Export citation
A TAIL CONE VERSION OF THE HALPERN–LÄUCHLI THEOREM AT A LARGE CARDINAL
-
- Published online by Cambridge University Press:
- 08 April 2019, pp. 473-496
-
- Article
- Export citation
AMALGAMABLE DIAGRAM SHAPES
-
- Published online by Cambridge University Press:
- 05 February 2019, pp. 88-101
-
- Article
- Export citation
PSEUDOFINITE H-STRUCTURES AND GROUPS DEFINABLE IN SUPERSIMPLE H-STRUCTURES
-
- Published online by Cambridge University Press:
- 02 April 2019, pp. 937-956
-
- Article
- Export citation
BEING LOW ALONG A SEQUENCE AND ELSEWHERE
-
- Published online by Cambridge University Press:
- 25 January 2019, pp. 497-516
-
- Article
- Export citation
A PARAMETRIC, RESOURCE-BOUNDED GENERALIZATION OF LÖB’S THEOREM, AND A ROBUST COOPERATION CRITERION FOR OPEN-SOURCE GAME THEORY
-
- Published online by Cambridge University Press:
- 02 April 2019, pp. 1368-1381
-
- Article
- Export citation
A SEPARATION RESULT FOR COUNTABLE UNIONS OF BOREL RECTANGLES
-
- Published online by Cambridge University Press:
- 22 February 2019, pp. 517-532
-
- Article
- Export citation
THE DP-RANK OF ABELIAN GROUPS
-
- Published online by Cambridge University Press:
- 01 February 2019, pp. 957-986
-
- Article
- Export citation
PURE INDUCTIVE LOGIC WITH FUNCTIONS
-
- Published online by Cambridge University Press:
- 08 April 2019, pp. 1382-1402
-
- Article
- Export citation
UNSOUND INFERENCES MAKE PROOFS SHORTER
-
- Published online by Cambridge University Press:
- 14 March 2019, pp. 102-122
-
- Article
- Export citation