Article contents
MARKOV’S PRINCIPLE AND SUBSYSTEMS OF INTUITIONISTIC ANALYSIS
Published online by Cambridge University Press: 26 February 2019
Abstract
Using a technique developed by Coquand and Hofmann [3] we verify that adding the analytical form MP1: 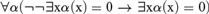 $\forall \alpha (\neg \neg \exists {\rm{x}}\alpha ({\rm{x}}) = 0 \to \exists {\rm{x}}\alpha ({\rm{x}}) = 0)$ of Markov’s Principle does not increase the class of
$\forall \alpha (\neg \neg \exists {\rm{x}}\alpha ({\rm{x}}) = 0 \to \exists {\rm{x}}\alpha ({\rm{x}}) = 0)$ of Markov’s Principle does not increase the class of 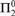 ${\rm{\Pi }}_2^0$ formulas provable in Kleene and Vesley’s formal system for intuitionistic analysis, or in subsystems obtained by omitting or restricting various axiom schemas in specified ways.
${\rm{\Pi }}_2^0$ formulas provable in Kleene and Vesley’s formal system for intuitionistic analysis, or in subsystems obtained by omitting or restricting various axiom schemas in specified ways.
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019
References
REFERENCES
- 1
- Cited by




