Research Article
The cylindric algebras of three-valued logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1201-1217
-
- Article
- Export citation
Relative constructivity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1218-1238
-
- Article
- Export citation
Filtral powers of structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1239-1254
-
- Article
- Export citation
Equivalence elementaire et decidabilite pour des structures du type groupe agissant sur un groupe abelien
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1255-1285
-
- Article
- Export citation
Termination and confluence in infinitary term rewriting
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1286-1296
-
- Article
- Export citation
Invisible genericity and 0#
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1297-1318
-
- Article
- Export citation
Bounding minimal degrees by computably enumerable degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1319-1347
-
- Article
- Export citation
How is it that infinitary methods can be applied to finitary mathematics? Gödel's T: a case study
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1348-1370
-
- Article
- Export citation
Compactness of Lobe spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1371-1392
-
- Article
- Export citation
The complexity of the core model
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1393-1398
-
- Article
- Export citation
Foundation versus induction in Kripke-Platek set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1399-1403
-
- Article
- Export citation
The least measurable can be strongly compact and indestructible
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1404-1412
-
- Article
- Export citation
The shuffle Hopf algebra and noncommutative full completeness
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1413-1436
-
- Article
- Export citation
Preserving σ-ideals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1437-1441
-
- Article
- Export citation
Quantifier elimination for neocompact sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1442-1472
-
- Article
- Export citation
CM-triviality and stable groups
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1473-1495
-
- Article
- Export citation
Large cardinals and large dilators
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1496-1510
-
- Article
- Export citation
Weakly o-minimal structures and some of their properties
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1511-1528
-
- Article
- Export citation
The interpretation of unsolvable λ-terms in models of untyped λ-calculus
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1529-1548
-
- Article
- Export citation
Rectangular games
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1549-1564
-
- Article
- Export citation



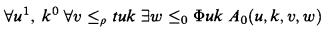
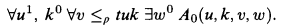
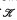 be an elementary class closed under updirected unions (e.g., if
be an elementary class closed under updirected unions (e.g., if 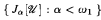 of countable initial segments of the core model
of countable initial segments of the core model 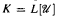 is definable over
is definable over 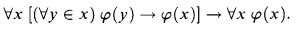
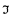 on
on 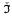 is not proper.
is not proper.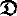 , we show that any unsolvable term admitting a decoration and having a non-empty interpretation in
, we show that any unsolvable term admitting a decoration and having a non-empty interpretation in 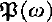 of Plotkin and Scott, Engeler's model
of Plotkin and Scott, Engeler's model 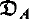 and Park's model
and Park's model 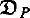 . We show that
. We show that