Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-25T06:36:42.915Z Has data issue: false hasContentIssue false
  • English
  • Français

The interpretation of unsolvable λ-terms in models of untyped λ-calculus

Published online by Cambridge University Press:  12 March 2014

Rainer Kerth
Rainer Kerth*
Affiliation:
Equipe de Logique Mathematique, Case 7012, Université Paris7, Denis Diderot, 2, Place Jussieu, 75690 Paris, France. E-mail:kerth@logique.jussieu.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Our goal in this paper is to analyze the interpretation of arbitrary unsolvable λ-terms in a given model of λ-calculus. We focus on graph models and (a special type of) stable models. We introduce the syntactical notion of a decoration and the semantical notion of a critical sequence. We conjecture that any unsolvable term β-reduces to a term admitting a decoration. The main result of this paper concerns the interconnection between those two notions: given a graph model or stable model 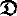, we show that any unsolvable term admitting a decoration and having a non-empty interpretation in 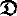generates a critical sequence in the model.

In the last section, we examine three classical graph models, namely the model 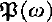of Plotkin and Scott, Engeler's model 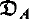and Park's model 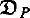. We show that 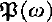and 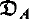do not contain critical sequences wherea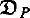s does.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 63 , Issue 4 , December 1998 , pp. 1529 - 1548
Copyright
Copyright © Association for Symbolic Logic 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Baeten, J. and Boerboom, B., Ω can be anything it should not be, Indagationes Mathematicae, vol. 41 (1979), pp. 111–120.Google Scholar
[2] Barendregt, H., Some extensional term models for combinatory logic and λ-calculi, Ph.D. thesis , University of Utrecht, 1971.Google Scholar
[3] Barendregt, H., The λ-calculus. its syntax and semantics, revised ed., North-Holland, Amsterdam, 1984.Google Scholar
[4] Barendregt, H., Representing ‘undefined’ in lambda calculus, Journal of Functional Programming, vol. 2 (1992), pp. 367–374, Theoretical Pearls.Google Scholar
[5] Berry, G., Stable models of typed λ-calculi, Proceedings of ICALP, Lecture Notes in Computer Science, vol. 62, 1978, pp. 72–89.Google Scholar
[6] Bucciarelli, A. and Ehrhard, T., Sequentiality and strong stability, Proceedings logic in computer science, Amsterdam, 1991.Google Scholar
[7] David, R., Every unsolvable λ-term has a decoration, to be published.Google Scholar
[8] Engeler, E., Algebras and combinators, Algebra Universalis, vol. 13 (1981), no. 3, pp. 389–392.Google Scholar
[9] Girard, J.-Y., The system F of variable types, fifteen years later, Theoretical Computer Science, vol. 45 (1986), pp. 159–192.CrossRefGoogle Scholar
[10] Hindley, J. R. and Longo, G., Lambda calculus models and extensionality, Zeitschrift für Logik und Grundlagen der Mathematik, vol. 26 (1980), pp. 289–310.Google Scholar
[11] Honsell, F. and Rocca, S. Ronchi Della, Reasoning about interpretations in qualitative λ-models, Proceedings of the IFIP conference programming concepts and methods (Broy, M. and Jones, C., editors), North-Holland, Amsterdam, 1990.Google Scholar
[12] Honsell, F. and Rocca, S. Ronchi Della, An approximation theorem for topological lambda models and the topological incompleteness of lambda calculus, Journal of Computer and System Sciences, vol. 45 (1992), pp. 49–75.Google Scholar
[13] Hyland, M., A syntactic characterization of the equality in some models for the lambda calculus, Journal of the London Mathematical Society, vol. 12 (1976), no. 2, pp. 361–370.Google Scholar
[14] Kerth, R., Forcing in stable models of untyped λ-calculus, accepted for publication in Indagationes Mathematicae.Google Scholar
[15] Kerth, R., Isomorphism and equational equivalence of continuous λ-models, accepted for publication in the Proceedings of the ASL Logic Colloquium '94.Google Scholar
[16] Kerth, R., On the construction of stable models of untyped λ-calculus, accepted for publication in Theoretical Computer Science.Google Scholar
[17] Kerth, R., Isomorphisme et équivalence équationnelle entre modèles du λ-calcul, Ph.D. thesis , Université Paris 7, 1995.Google Scholar
[18] Krivine, J. L., Lambda-calculus, types and models, Ellis Horwood, Hemel Hempstead, 1993.Google Scholar
[19] Longo, G., Set-theoretical models of λ-calculus: Theories, expansions, isomorphisms, Annals of Pure and Applied Logic, vol. 24 (1983), pp. 153–188.Google Scholar
[20] Meyer, A., What is a model of the lambda-calculus?, Information and Control, vol. 52 (1982), pp. 87–122.Google Scholar
[21] Morris, J. H., Lambda-calculus models of programming languages, Ph.D. thesis , Sloan School of Management, MIT, 1968, MAC Reprint TR-57, Massachusetts Institute of Technology, Cambridge, Massachusetts.Google Scholar
[22] Park, D., The Y-combinator in Scott's lambda calculus models, Theory of Computation Report 13, University of Warwick, Department of Computer Science, 1976.Google Scholar
[23] Plotkin, G., A set-theoretical definition of application, Memorandum mip-r-95, School of Artificial Intelligence, University of Edinburgh, 1972, published as the first part of Set-theoretical and Other Elementary Models of the λ-Calculus, Theoretical Computer Science, vol. 121, no. 1–2, 1993, pp. 351–410.Google Scholar
[24] Scott, D. S., Models for the λ-calculus, unpublished manuscript, 1969.Google Scholar
[25] Scott, D. S., Continuous lattices, Toposes, algebraic geometry and logic (Lawvere, F.W., editor). Lecture Notes in Mathematics, vol. 274, Springer-Verlag, Berlin, 1972, pp. 97–136.Google Scholar
[26] Scott, D. S., Data types as lattices, SIAM Journal of Computing, vol. 5 (1976), no. 3, pp. 522–587.Google Scholar
[27] Wadsworth, C. P., Semantics and pragmatics of the lambda-calculus, Ph.D. thesis , Oxford University, 1971.Google Scholar
[28] Wadsworth, C. P., Approximate reduction and λ-calculus models, SIAM Journal of Computing, vol. 7 (1978), no. 3, pp. 337–356.Google Scholar
[29] Zylberajch, C., Syntaxe et sémantique de la facilité en λ-calcul, Ph.D. thesis , Université Paris 7, 1991.Google Scholar