Research Article
An application of ultrapowers to changing cofinality
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 225-235
-
- Article
- Export citation
Further consistency and independence results in NF obtained by the permutation method
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 236-238
-
- Article
- Export citation
Paires de structures stables
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 239-249
-
- Article
- Export citation
Large families of incomparable A-isols
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 250-252
-
- Article
- Export citation
On cofinal extensions of models of arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 253-262
-
- Article
- Export citation
Set theory with a filter quantifier
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 263-287
-
- Article
- Export citation
Forcing and reducibilities
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 288-310
-
- Article
- Export citation
A certain class of models of Peano arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 311-320
-
- Article
- Export citation
A complete theory with arbitrarily large minimality ranks
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 321-328
-
- Article
- Export citation
Boolean sentence algebras: Isomorphism constructions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 329-338
-
- Article
- Export citation
Groupes stables, avec types génériques réguliers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 339-355
-
- Article
- Export citation
High and low Kleene degrees of coanalytic sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 356-368
-
- Article
- Export citation
R. e. presented linear orders
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 369-376
-
- Article
- Export citation
Countable models of multidimensional ℵ0-stable theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 377-383
-
- Article
- Export citation
Compactness of a supervaluational language
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 384-386
-
- Article
- Export citation
The monadic theory of ω21
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 387-398
-
- Article
- Export citation
The slow-growing and the Graegorczyk hierarchies
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 399-408
-
- Article
- Export citation
A characterization of 2-square Ultrafilters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 409-414
-
- Article
- Export citation
Completeness in the theory of properties, relations, and propositions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 415-426
-
- Article
- Export citation
Some useful preservation theorems
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 427-440
-
- Article
- Export citation



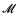 (
(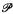 (
(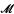 with an ability to perform a countably infinite sequence of program steps in finite time and with oracles for
with an ability to perform a countably infinite sequence of program steps in finite time and with oracles for 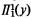
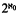 nonisomorphic and non-almost-homogeneous countable models. The same type of construction has been used before to show that if
nonisomorphic and non-almost-homogeneous countable models. The same type of construction has been used before to show that if 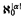 nonisomorphic models of cardinality ℵ
nonisomorphic models of cardinality ℵ