Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-10T02:32:24.332Z Has data issue: false hasContentIssue false
  • English
  • Français

High and low Kleene degrees of coanalytic sets

Published online by Cambridge University Press:  12 March 2014

Stephen G. Simpson  and
Galen Weitkamp
Stephen G. Simpson
Affiliation:
Pennsylvania State University, University Park, Pennsylvania 16802
Galen Weitkamp
Affiliation:
Western Illinois University, Macomb, Illinois 61455
Get access Rights & Permissions [Opens in a new window]

Extract

We say that a set A of reals is recursive in a real y together with a set B of reals if one can imagine a computing machine 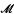with an ability to perform a countably infinite sequence of program steps in finite time and with oracles for B and y so that 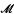decides membership in A for any real x input to 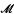by way of an oracle for x. We write A ≤ yB. A precise definition of this notion of recursion was first considered in Kleene [9]. In the notation of that paper, A ≤yB if there is an integer e so that χA(x) = {e}(x y, χB, 2E). Here χA is the characteristic function of A. Thus Kleene would say that A is recursive in (y, B, 2E), where 2E is the existential integer quantifier.

Gandy [5] observes that the halting problem for infinitary machines such as 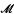, as in the case of Turing machines, gives rise to a jump operator for higher type recursion. Thus given a set B of reals, the superjump B′ of B is defined to be the set of all triples 〈e, x, y〉 such that the eth machine with oracles for y and B eventually halts when given input x. A set A is said to be semirecursive in y together with B if for some integer e, A is the cross section {x: 〈e, x, y 〉 ∈ B′}. In Kleene [9] it is demonstrated that a set A is semirecursive in y alone if and only if it is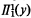

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 2 , June 1983 , pp. 356 - 368
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barwise, K.J., Admissible sets and structures, Springer, Berlin, 1975.CrossRefGoogle Scholar
[2]Boolos, G. and Putnam, H., Degrees of tmsolvability of constructible sets of integers, this Journal, vol. 33 (1968), pp. 497–513.Google Scholar
[3]Devlin, K., Forcing over admissible sets and a theorem on countable sequences of admissibles (edited Jensen notes), 1972, manuscript.Google Scholar
[4]Devlin, K. and Paris, J., Certain sequences of ordinals, Finite and infinite sets, vol. 10, Colloquia Mathematica Societas Janos Bolyai, Keszthely (Hungary), 1973, pp. 333–360.Google Scholar
[5]Gandy, R.O., General recursive Junctionals of finite types and hierarchies of functionals, Annales Scientifiques de l'Université de Clermont. Série Mathématique, No. 35 (1967), pp. 5–24.Google Scholar
[6]Harrington, L., Analytic determinacy and 0#, this Journal, vol. 43 (1978), pp. 685–693.Google Scholar
[7]Hrbacek, K., On the complexity of analytic sets, Zeitsckrift für Mathematische Logik und Grundlagen der Mathematik, vol. 24 (1978), pp. 419–425.CrossRefGoogle Scholar
[8]Hrbacek, K. and Simpson, S.G., On Kleene degrees of analytic sets, Kleene Symposium, North-Holland, Amsterdam, 1980, pp. 269–273.Google Scholar
[9]Kleene, S.C., Recursive functionals and quantifiers of finite types. I, II, Transactions of the American Mathematical Society, vol. 91 (1959), pp. 1–52; vol. 108 (1963), pp. 106–142.Google Scholar
[10]Mansfield, R.B. and Weitkamp, G., Descriptive set theory, Oxford Logic Guides (Scott, D., Editor), Oxford University Press (to appear).Google Scholar
[11]Posner, D.B., A survey of non-RE degrees ≤0′, Recursion theory: Its generalizations and applications, Proceedings of Logic Colloquium '79, (Drake, F.R. and Wainer, S.S., Editor), London Mathematical Society Lecture Notes, vol. 45, 1980, pp. 52–109.Google Scholar
[12]Sacks, G.E., E-recursion theory, handwritten notes by Griffor, E., Harvard University, Spring 1980, 80 pp.Google Scholar
[13]Simpson, S.G., Degrees of unsolvability: a survey of results, Handbook of Mathematical Logic, North-Holland, Amsterdam, 1977, pp. 631–652.CrossRefGoogle Scholar
[14]Soare, R.I., Recursively enumerable sets and degrees. Bulletin of the American Mathematical Society, vol. 84 (1978), pp. 1149–1181.CrossRefGoogle Scholar
[15]Solovay, R., Determinacy and type 2 recursion (abstract), this Journal, vol. 36 (1971), p. 374.Google Scholar
[16]Stern, J., Definable families of Borel sets of bounded rank, manuscript, 1980 (to appear).Google Scholar
[17]Weitkamp, G., Kleene recursion over the continuum, Ph.D. thesis, Pennsylvania State University, 1980.Google Scholar