Research Article
On spectra of sentences of monadic second order logic with counting
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 617-640
-
- Article
- Export citation
Lovely pairs of models: the non first order case
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 641-662
-
- Article
- Export citation
The complexity of continuous embeddability between dendrites
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 663-673
-
- Article
- Export citation
On some small cardinals for Boolean algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 674-682
-
- Article
- Export citation
Reverse mathematics and the equivalence of definitions for well and better quasi-orders
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 683-712
-
- Article
- Export citation
Every polynomial-time 1-degree collapses if and only if P = PSPACE
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 713-741
-
- Article
- Export citation
Solovay models and forcing extensions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 742-766
-
- Article
- Export citation
Patterns of paradox
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 767-774
-
- Article
- Export citation
Leibnizian models of set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 775-789
-
- Article
- Export citation
On the intuitionistic strength of monotone inductive definitions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 790-798
-
- Article
- Export citation
Continuum-many Boolean algebras of the form
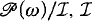 Borel
Borel
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 799-816
-
- Article
- Export citation
Dividing in the algebra of compact operators
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 817-829
-
- Article
- Export citation
Wellfoundedness proofs by means of non-monotonic inductive definitions I: Π20-operators
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 830-850
-
- Article
- Export citation
Diophantine properties of sets definable in o-minimal structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 851-861
-
- Article
- Export citation
On the construction of effectively random sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 862-878
-
- Article
- Export citation
Filtering unification and most general unifiers in modal logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 879-906
-
- Article
- Export citation
Every 2-random real is Kolmogorov random
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 907-913
-
- Article
- Export citation
Almost everywhere domination
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 914-922
-
- Article
- Export citation
Theories of presheaf type
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 923-934
-
- Article
- Export citation
Other
Retraction note for “PDL has interpolation”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 935-936
-
- Article
- Export citation



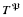 whose saturated models are the lovely pairs of
whose saturated models are the lovely pairs of 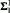 -complete. We also show that embeddability between countable linear orders with infinitely many colors is
-complete. We also show that embeddability between countable linear orders with infinitely many colors is 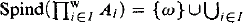 Spind(
Spind(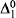 formulas and adding a formula induction scheme for
formulas and adding a formula induction scheme for 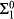 formulas. For the purposes of this paper, we will be concerned with fairly weak extensions of RCA
formulas. For the purposes of this paper, we will be concerned with fairly weak extensions of RCA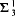 absolutely-ccc forcing extension, and that this is essentially the optimal preservation result, i.e., it does not hold for
absolutely-ccc forcing extension, and that this is essentially the optimal preservation result, i.e., it does not hold for 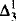 absolutely-ccc forcing notions. We extend these results to the higher projective classes of ccc posets, and to the class of all projective ccc posets, using definably-Mahlo cardinals. As a consequence we obtain an exact equiconsistency result for generic absoluteness under projective absolutely-ccc forcing notions.
absolutely-ccc forcing notions. We extend these results to the higher projective classes of ccc posets, and to the class of all projective ccc posets, using definably-Mahlo cardinals. As a consequence we obtain an exact equiconsistency result for generic absoluteness under projective absolutely-ccc forcing notions.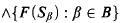
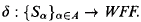
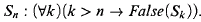
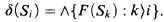
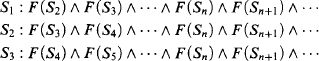
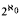 nonisomorphic countable Leibnizian models
nonisomorphic countable Leibnizian models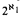 nonisomorphic Leibnizian models
nonisomorphic Leibnizian models 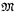 of T of power
of T of power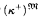
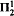 –CA
–CA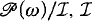 Borel
Borel
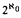 ; earlier work by Ilijas Farah had shown that this was the value in models of Martin's Maximum or some similar forcing axiom, but it was open whether there could be fewer in models of the Continuum Hypothesis.
; earlier work by Ilijas Farah had shown that this was the value in models of Martin's Maximum or some similar forcing axiom, but it was open whether there could be fewer in models of the Continuum Hypothesis.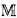 be an o-minimal expansion of the ordered field of real numbers
be an o-minimal expansion of the ordered field of real numbers 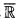 , and let
, and let 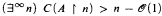 . where
. where 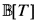 is (equivalent to) a presheaf topos. (We adhere to the convention that
is (equivalent to) a presheaf topos. (We adhere to the convention that 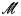 , the following properties are equivalent
, the following properties are equivalent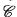 of finitely presentable objects
of finitely presentable objects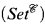 , the category of points of some presheaf topos
, the category of points of some presheaf topos