Article contents
Solovay models and forcing extensions
Published online by Cambridge University Press: 12 March 2014
Abstract.
We study the preservation under projective ccc forcing extensions of the property of L(ℝ) being a Solovay model. We prove that this property is preserved by every strongly-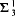 absolutely-ccc forcing extension, and that this is essentially the optimal preservation result, i.e., it does not hold for
absolutely-ccc forcing extension, and that this is essentially the optimal preservation result, i.e., it does not hold for 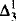 absolutely-ccc forcing notions. We extend these results to the higher projective classes of ccc posets, and to the class of all projective ccc posets, using definably-Mahlo cardinals. As a consequence we obtain an exact equiconsistency result for generic absoluteness under projective absolutely-ccc forcing notions.
absolutely-ccc forcing notions. We extend these results to the higher projective classes of ccc posets, and to the class of all projective ccc posets, using definably-Mahlo cardinals. As a consequence we obtain an exact equiconsistency result for generic absoluteness under projective absolutely-ccc forcing notions.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2004
References
REFERENCES
- 7
- Cited by


