Article contents
Continuum-many Boolean algebras of the form 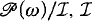 Borel
Borel
Published online by Cambridge University Press: 12 March 2014
Abstract.
We examine the question of how many Boolean algebras, distinct up to isomorphism, that are quotients of the powerset of the naturals by Borel ideals, can be proved to exist in ZFC alone. The maximum possible value is easily seen to be the cardinality of the continuum 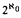 ; earlier work by Ilijas Farah had shown that this was the value in models of Martin's Maximum or some similar forcing axiom, but it was open whether there could be fewer in models of the Continuum Hypothesis.
; earlier work by Ilijas Farah had shown that this was the value in models of Martin's Maximum or some similar forcing axiom, but it was open whether there could be fewer in models of the Continuum Hypothesis.
We develop and apply a new technique for constructing many ideals whose quotients must be nonisomorphic in any model of ZFC. The technique depends on isolating a kind of ideal, called shallow, that can be distinguished from the ideal of all finite sets even after any isomorphic embedding, and then piecing together various copies of the ideal of all finite sets using distinct shallow ideals. In this way we are able to demonstrate that there are continuum-many distinct quotients by Borel ideals, indeed by analytic P-ideals, and in fact that there is in an appropriate sense a Borel embedding of the Vitali equivalence relation into the equivalence relation of isomorphism of quotients by analytic P-ideals. We also show that there is an uncountable definable wellordered collection of Borel ideals with distinct quotients.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2004
References
REFERENCES
- 4
- Cited by


