Spanwise arrays of miniature vortex generators (MVGs) are used to generate energetic transient disturbance growth, which is able to modulate the boundary layer flow with steady and stable streak amplitudes up to 32 % of the free-stream velocity. This type of modulation has previously been shown to act in a stabilizing manner on modal disturbance growth described by classical instability theory. In an attempt to reproduce a more realistic flow configuration, in the present experimental set-up, Tollmien–Schlichting (TS) waves are generated upstream of the MVG array, allowing for a complete interaction of the incoming wave with the array. Fifteen new MVG configurations are investigated and the stabilizing effect on the TS waves is quantified. We show that the streak amplitude definition is very important when trying to relate it to the stabilization, since it may completely bypass information on the mean streamwise velocity gradient in the spanwise direction, which is an essential ingredient of the observed stabilization. Here, we use an integral-based streak amplitude definition along with a streak amplitude scaling relation based on empiricism, which takes the spanwise periodicity of the streaks into account. The results show that, applying the integral definition, the optimal streak amplitude for attenuating TS wave disturbance growth is around 30 % of the free-stream velocity, which corresponds to ${\sim }20\hspace{0.167em} \% $ in the conventional definition when keeping the spanwise wavelength constant. The experiments also show that the disturbance energy level, based on the full velocity signal, is significantly reduced in the controlled case, and that the onset of transition may be inhibited altogether throughout the measured region in the presence of an MVG array.

Natural convection in an infinite horizontal layer subject to periodic heating along the lower wall has been investigated using a combination of numerical and asymptotic techniques. The heating maintains the same mean temperatures at both walls while producing sinusoidal temperature variations along one horizontal direction, with its spatial distribution characterized by the wavenumber $\alpha $ and the amplitude expressed in terms of a Rayleigh number $R{a}_{p} $. The primary response of the system takes the form of stationary convection consisting of rolls with the axis orthogonal to the heating wave vector and structure determined by the particular values of $R{a}_{p} $ and $\alpha $. It is shown that for sufficiently large $\alpha $ convection is limited to a thin layer adjacent to the lower wall with a uniform conduction zone emerging above it; the temperature in this zone becomes independent of the heating pattern and varies in the vertical direction only. Linear stability of the above system has been considered and conditions leading to the emergence of secondary convection have been identified. Secondary convection gives rise to either longitudinal rolls, transverse rolls or oblique rolls at the onset, depending on $\alpha $. The longitudinal rolls are parallel to the primary rolls and the transverse rolls are orthogonal to the primary rolls, and both result in striped patterns. The oblique rolls lead to the formation of convection cells with aspect ratio dictated by their inclination angle and formation of rhombic patterns. Two mechanisms of instability have been identified. In the case of $\alpha = O(1)$, parametric resonance dominates and leads to a pattern of instability that is locked in with the pattern of heating according to the relation ${\delta }_{cr} = \alpha / 2$, where ${\delta }_{cr} $ denotes the component of the critical disturbance wave vector parallel to the heating wave vector. The second mechanism, the Rayleigh–Bénard (RB) mechanism, dominates for large $\alpha $, where the instability is driven by the uniform mean vertical temperature gradient created by the primary convection, with the critical disturbance wave vector ${\delta }_{cr} \rightarrow 1. 56$ for $\alpha \rightarrow \infty $ and the fluid response becoming similar to that found in the case of a uniformly heated wall. Competition between these mechanisms gives rise to non-commensurable states in the case of longitudinal rolls and the appearance of soliton lattices, to the formation of distorted transverse rolls, and to the appearance of the wave vector component in the direction perpendicular to the forcing direction. A rapid stabilization is observed when the heating wavenumber is reduced below $\alpha \approx 2. 2$ and no instability is found when $\alpha \lt 1. 6$ in the range of $R{a}_{p} $ considered. It is shown that $\alpha $ plays the role of an effective pattern control parameter and its judicious selection provides a means for the creation of a wide range of flow responses.

The combined effects of axial flow and eccentricity on the temporal stability properties of the Taylor–Couette system are investigated using a pseudospectral method. Eccentricity is found to stabilize the Couette flow regardless of axial advection intensity. As the axial Reynolds number ${\mathit{Re}}_{z} $ is increased for any fixed eccentricity $e\leq 0. 7$, the critical mode switches from deformed toroidal Taylor vortices to helical structures with an increasing number of waves, and with helicity opposed to the inner-cylinder rotation. For a wide-gap configuration of radius ratio $\eta = 0. 5$, increasing axial advection has a stabilizing effect for low ${\mathit{Re}}_{z} $, then a weak destabilizing effect for high enough ${\mathit{Re}}_{z} $. Centrifugal effects are always destabilizing, but axial shear is responsible for the dominance of helical modes of increasing azimuthal complexity. The modes localize in the converging gap region, and the energy concentrates increasingly into axial motion for larger ${\mathit{Re}}_{z} $. Critical quantities are also computed for a small-gap case, and similar trends are observed, even though no destabilizing effect of advection is observed within the range of ${\mathit{Re}}_{z} $ considered. Comparison with the experiment of Coney & Mobbs (Proc. Inst. Mech. Engrs, vol. 184 Pt 3L, 1969–70, pp. 10–17) for $\eta = 0. 89$ shows good agreement, despite small discrepancies attributed to finite length effects.

We use computer simulations and an analytical model to study the relationship between kinematics and performance in jet-propelled jellyfish swimming. We prescribe different power-law kinematics for the bell contraction and expansion, and identify kinematics that yield high swimming speeds and/or high efficiency. In the simulations, high efficiency is found when the bell radius is a nearly linear function of time, and in a second case corresponding to ‘burst-and-coast’ kinematics. The analytical model studies the contraction phase only, and finds that the efficiency-optimizing bell radius as a function of time transitions from nearly linear (similar to the numerics) for small-to-moderate output power to exponentially decaying for large output power.

Numerical simulations and laboratory experiments were jointly conducted to investigate a bathtub vortex under the influence of a protruding cylinder in a rotating tank. In the set-up, a central drain hole is placed at the bottom of the tank and a top-down cylinder is suspended from the rigid top lid, with fluid supplied from the sidewall for mass conservation. The cylinder is protruded to produce the Taylor column effect. The flow pattern depends on the Rossby number ($\mathit{Ro}= U/ fR$), the Ekman number ($\mathit{Ek}= \nu / f{R}^{2} )$ and the height ratio, $h/ H$, where $R$ is the radius of the cylinder, $f$ is the Coriolis parameter, $\nu $ is the kinematic viscosity of the fluid, $h$ is the vertical length of the cylinder and $H$ is the height of the tank. It is found appropriate to choose $U$ to be the average inflow velocity of fluid entering the column beneath the cylinder. Steady-state solutions obtained by numerically solving the Navier–Stokes equations in the rotating frame are shown to have a good agreement with flow visualizations and particle tracking velocimetry (PTV) measurements. It is known that at $\mathit{Ro}\sim 1{0}^{- 2} $, the central downward flow surrounded by the neighbouring Ekman pumping forms a classic one-celled bathtub vortex structure when there is no protruding cylinder ($h/ H= 0$). The influence of a suspended cylinder ($h/ H\not = 0$) leads to several findings. The bathtub vortex exhibits an interesting two-celled structure with an inner Ekman pumping (EP) and an outer up-drafting motion, termed Taylor upwelling (TU). The two regions of up-drafting motion are separated by a notable finite-thickness structure, identified as a (thin-walled) Taylor column. The thickness ${ \delta }_{T}^{\ast } $ of the Taylor column is found to be well correlated to the height ratio and the Ekman number by ${\delta }_{T} = { \delta }_{T}^{\ast } / R= {(1- h/ H)}^{- 0. 32} {\mathit{Ek}}^{0. 095} $. The Taylor column presents a barrier to the fluid flow such that the fluid from the inlet may only flow into the inner region through the narrow gaps, one above the Taylor column and one beneath it (conveniently called Ekman gaps). As a result, five types of routes along which the fluid may flow to and exit at the drain hole could be identified for the multi-celled vortex structure. Moreover, the flow rates associated with the five routes were calculated and compared to help understand the relative importance of the component flow structures. The weaker influence of the Taylor column effect on the bathtub vortex at $\mathit{Ro}\sim 1$ or even higher $\mathit{Ro}\sim 1{0}^{2} $ is also discussed.

Turbulence governed by the Navier–Stokes equations shows a tendency to evolve towards a state in which the nonlinearity is diminished. In fully developed turbulence, this tendency can be measured by comparing the variance of the nonlinear term to the variance of the same quantity measured in a Gaussian field with the same energy distribution. In order to study this phenomenon at high Reynolds numbers, a version of the direct interaction approximation is used to obtain a closed expression for the statistical average of the mean-square nonlinearity. The wavenumber spectrum of the mean-square nonlinear term is evaluated and its scaling in the inertial range is investigated as a function of the Reynolds number. Its scaling is dominated by the sweeping by the energetic scales, but this sweeping is weaker than predicted by a random sweeping estimate. At inertial range scales, the depletion of nonlinearity as a function of the wavenumber is observed to be constant. At large scales it is observed that the mean-square nonlinearity is larger than its Gaussian estimate, which is shown to be related to the non-Gaussianity of the Reynolds-stress fluctuations at these scales.

Particle capture, whereby suspended particles contact and adhere to a solid surface (a ‘collector’), is an important mechanism for a range of environmental processes including suspension feeding by corals and ‘filtering’ by aquatic vegetation. In this paper, we use two- and three-dimensional direct numerical simulations to quantify the capture efficiency ($\eta $) of low-inertia particles by a circular cylindrical collector at intermediate Reynolds numbers in the vortex-shedding regime (i.e. for $47\lt \mathit{Re}\leq 1000$, where $\mathit{Re}$ is the collector Reynolds number). We demonstrate that vortex shedding induces oscillations near the leading face of the collector which greatly affect the quantity and distribution of captured particles. Unlike in steady, low-$\mathit{Re}$ flow, particles directly upstream of the collector are not the most likely to be captured. Our results demonstrate the dependence of the time-averaged capture efficiency on $\mathit{Re}$ and particle size, improving the predictive capability for the capture of particles by aquatic collectors. The transition to theoretical high-Reynolds-number behaviour (i.e. $\eta \sim {\mathit{Re}}^{1/ 2} $) is complex due to comparatively rapid changes in wake conditions in this Reynolds number range.

Sustained friction drag reduction and heat transfer augmentation are simultaneously achieved in a fully developed channel flow where the averaged transport equations and wall boundary conditions for momentum and heat have identical form. Zero-net-mass-flux wall blowing and suction is assumed as a control input and its spatio-temporal distribution is determined based on optimal control theory. When the root-mean-square value of the control input is 5 % of the bulk mean velocity, the friction drag is decreased by 24 % from the uncontrolled value, whereas the heat transfer is more than doubled. Optimizations with different amplitudes of the control input and different Reynolds numbers reveal that the optimal control inputs commonly exhibit the property of a downstream travelling wave, whose wavelength is ∼250 in wall units and phase velocity is ∼30 % of the bulk mean velocity. Detailed analyses of the controlled velocity and thermal fields show that the travelling wave input contributes to dissimilar heat transfer enhancement through two distinct mechanisms, i.e. direct modification of the coherent velocity and thermal fields and an indirect effect on the random fields. The present results show that the divergence-free velocity vector and the conservative scalar are essentially different, and this is a key to achieving dissimilar heat transfer enhancement in turbulent shear flows.

A large database of new direct numerical simulations of forced compressible turbulence on up to $204{8}^{3} $ grids, and a range of Reynolds (${R}_{\lambda } $) and turbulent Mach (${M}_{t} $) numbers, is analysed to study the scaling of pressure, density and temperature fluctuations. Small-perturbation analysis is used to study the scaling of variances, and different cross-correlations as well as spectra. Qualitative differences are observed between low and high ${M}_{t} $. The probability density functions (p.d.f.s) of pressure and density are negatively skewed at low ${M}_{t} $ (consistent with incompressible results) but become positively skewed at high ${M}_{t} $. The positive tails are found to follow a log-normal distribution. A new variable is introduced to quantify departures from isentropic fluctuations (an assumption commonly used in the literature) and is found to increase as ${ M}_{t}^{2} $. However, positive fluctuations of pressure and density tend to be more isentropic than negative fluctuations. In general, Reynolds number effects on single-point statistics are observed to be weak. The spectral behaviour of pressure, density and temperature is also investigated. While at low ${M}_{t} $, pressure appears to scale as ${k}^{- 7/ 3} $ ($k$ is the wavenumber) in the inertial range as in incompressible flows, a ${k}^{- 5/ 3} $ scaling also appears to be consistent with the data at a range of Mach numbers. Density and temperature spectra are found to scale as ${k}^{- 5/ 3} $ for a range of Mach numbers.

Bioconvection is an important phenomenon in aquatic environments, affecting the spatial distribution of motile micro-organisms and enhancing mixing within the fluid. However, stratification arising from thermal or solutal gradients can play a pivotal role in suppressing the bioconvective flows, leading to the aggregation of micro-organisms and growth of their patchiness. We investigate the combined effects by considering gyrotactic motility where the up-swimming cells are directed by the balance of the viscous and gravitational torques. To study this system, we employ a continuum model consisting of Navier–Stokes equations with the Boussinesq approximation coupled with two conservation equations for the concentration of cells and stratification agent. We present a linear stability analysis to determine the onset of bioconvection for different flow parameters. Also, using large-scale numerical simulations, we explore different regimes of the flow by varying the corresponding boundary conditions and dimensionless variables such as Rayleigh number and Lewis number ($\mathit{Le}$) and we show that the cell distribution can be characterized using the ratio of the buoyancy forces as the determinant parameter when $\mathit{Le}\lt 1$ and the boundaries are insulated. But, in thermally stratified fluids corresponding to $\mathit{Le}\gt 1$, temperature gradients are demonstrated to have little impact on the bioconvective plumes provided that the walls are thermally insulated. In addition, we analyse the dynamical behaviour of the system in the case of persistent pycnoclines corresponding to constant salinity boundary conditions and we discuss the associated inhibition threshold of bioconvection in the light of the stability of linearized solutions.

The present paper deals with the generation of sound by the passage of acoustic or entropy perturbations through a nozzle in the nonlinear regime and in the low-frequency limit. The analytical model of Marble and Candel for compact nozzles (J. Sound Vib., vol. 55, 1977, pp. 225–243), initially developed for excitations in the linear regime, is rederived and extended to the nonlinear domain. Full nonlinear and second-order models are written for both subcritical and supercritical nozzles in the absence of shock and a detailed methodology is provided for the resolution of the second-order system. The accuracy of the second-order model is assessed for entropy forcings. It is shown to be accurate for all waves, with the exception of the upstream generated wave for subcritical diverging geometries where higher-order nonlinear contributions cannot be neglected. In the context of indirect combustion noise, the phenomenon of regime change of the nozzle due to an incoming entropy fluctuation is also addressed. Regime change is related to a Mach number modification induced by temperature and velocity fluctuations. In the present study, it translates into a limitation of the maximum amplitude of the incoming entropy forcing. Such limitations are to be considered for subcritical nozzles with significant inlet or outlet Mach numbers, where the flow transition is observed even for very low-amplitude entropy excitations. With the constraint of those limitations, the analytical extended nozzle describing functions representing the full nonlinear response for indirect combustion noise are validated through detailed comparisons with numerical simulations.

The characteristics of unbounded flow past an impulsively started planar energy extracting device, such as a wind or tidal turbine, are studied theoretically, numerically and experimentally. The initial thrust on an impulsively started device, which can be more than double the steady thrust, is an important consideration for design and safe operation. The energy sink is modelled here as an ‘actuator surface’ which imposes a uniform pressure discontinuity in the fluid proportional to the square of the fluid speed normal to the surface, the fluid density, and a dimensionless resistance coefficient. The flow past the actuator is studied theoretically for the case of weak resistance using an unsteady model which recovers steady linear momentum theory in the limit of long time. For the case of strong resistance the flow is studied numerically using the point vortex method. Experimental measurements of thrust on a mesh towed through static water are compared to the numerical results and show good agreement. The thrust on an impulsively started device is estimated, for a typical installation, to fall to within 10 % of the steady value within ∼1 min. The numerical model is also used to simulate the gradual startup of a device, yielding estimates of the time constant necessary in a control system in order to reduce peak thrusts in practice.

Compressibility profoundly affects many aspects of turbulence in high-speed flows, most notably stability characteristics, anisotropy, kinetic–potential energy interchange and spectral cascade rate. We develop a unified framework for modelling pressure-related compressibility effects by characterizing the role and action of pressure in different speed regimes. Rapid distortion theory is used to examine the physical connection between the various compressibility effects leading to model form suggestions for pressure–strain correlation, pressure–dilatation and dissipation evolution equations. The closure coefficients are established using fixed-point analysis by requiring consistency between model and DNS asymptotic behaviour in compressible homogeneous shear flow. The closure models are employed to compute high-speed mixing layers and boundary layers. The self-similar mixing-layer profile, increased Reynolds stress anisotropy and diminished mixing-layer growth rates with increasing Mach number are all well captured. High-speed boundary-layer results are also adequately replicated even without the use of advanced thermal-flux models or low-Reynolds-number corrections.

The streamwise vortices generated by dielectric-barrier-discharge plasma actuators in the laminar boundary layer were investigated using particle image velocimetry to understand the vortex-formation mechanisms. The plasma vortex generator was oriented along the primary flow direction to produce a body force in the spanwise direction. This created a spanwise-directed wall jet which interacted with the oncoming boundary layer to form a coherent streamwise vortex. It was found that the streamwise vortices were formed by the twisting and folding of the spanwise vorticity in the oncoming boundary layer into the outer shear layer of the spanwise wall jet, which added its own vorticity to increase the circulation along the actuator length. This is similar to the delta-shaped, vane-type vortex generator, except that the circulation was enhanced by the addition of the vorticity in the plasma jet. It was also observed that the plasma vortex was formed close to the wall with an enhanced wall-ward entrainment, which created strong downwash above the actuator.

We experimentally study linear and nonlinear waves on the surface of a fluid covered by an elastic sheet where both tension and flexural waves occur. An optical method is used to obtain the full space–time wave field, and the dispersion relation of the waves. When the forcing is increased, a significant nonlinear shift of the dispersion relation is observed. We show that this shift is due to an additional tension of the sheet induced by the transverse motion of a fundamental mode of the sheet. When the system is subjected to a random-noise forcing at large scales, a regime of hydroelastic wave turbulence is observed with a power-law spectrum of the scale, in disagreement with the wave turbulence prediction. We show that the separation between relevant time scales is well satisfied at each scale of the turbulent cascade as expected theoretically. The wave field anisotropy, and finite size effects are also quantified and are not at the origin of the discrepancy. Finally, the dissipation is found to occur at all scales of the cascade, contrary to the theoretical hypothesis, and could thus explain this disagreement.

Topological evolution of compressible turbulent boundary layers at Mach 2 is investigated by means of statistical analysis of the invariants of the velocity gradient tensor based on the direct numerical simulation database. The probability density functions of the rate of change of the invariants exhibit the $- 3$ power-law distribution in the region of large Lagrangian derivative of the invariants in the inner and outer layers. The topological evolution is studied by conditional mean trajectories for the evolution of the invariants. The trajectories illustrate inward-spiralling orbits around and converging to the origin of the space of invariants in the outer layer, while they are repelled by the vicinity of the origin and converge towards a limit cycle in the inner layer. The compressibility effect on the mean topological evolution is studied in terms of the ‘incompressible’, compressed and expanding regions. It is found that the mean evolution of flow topologies is altered by the compressibility. The evolution equations of the invariants are derived and the relevant dynamics of the mean topological evolution are analysed. The compressibility effect is mainly related to the pressure effect. The mutual-interaction terms among the invariants are the root of the clockwise spiral behaviour of the local flow topology in the space of invariants.

The inception of leading-edge stall on stationary, two-dimensional, smooth, thin aerofoils at low to moderately high chord Reynolds number flows is investigated by a reduced-order, multiscale model problem via numerical simulations. The asymptotic theory demonstrates that a subsonic flow about a thin aerofoil can be described in terms of an outer region, around most of the aerofoil’s chord, and an inner region, around the nose, that asymptotically match each other. The flow in the outer region is dominated by the classical thin aerofoil theory. Scaled (magnified) coordinates and a modified (smaller) Reynolds number 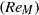$(R{e}_{M} )$ are used to correctly account for the nonlinear behaviour and extreme velocity changes in the inner region, where both the near-stagnation and high suction areas occur. It results in a model problem of a uniform, incompressible and viscous flow past a semi-infinite parabola with a far-field circulation governed by a parameter 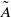$\tilde {A} $ that is related to the aerofoil’s angle of attack, nose radius of curvature, thickness ratio, and camber. The model flow problem is solved for various values of 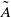$\tilde {A} $ through numerical simulations based on the unsteady Navier–Stokes equations. The value 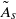${\tilde {A} }_{s} $ where a global separation zone first erupts in the nose flow, accompanied by loss of peak streamwise velocity ahead of it and change in shedding frequency behind it, is determined as a function of 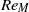$R{e}_{M} $. These values indicate the stall onset on the aerofoil at various flow conditions. It is found that 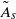${\tilde {A} }_{s} $ decreases with 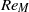$R{e}_{M} $ until some limit 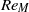$R{e}_{M} $ (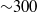${\sim }300$) and then increases with further increase of Reynolds number. At low values of 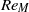$R{e}_{M} $ the flow is laminar and steady, even when stall occurs. The flow in this regime is dominated by the increasing effect of the adverse pressure gradient, which eventually overcomes the ability of the viscous stress to keep the boundary layer attached to the aerofoil. The change in the nature of stall at the limit 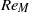$R{e}_{M} $ is attributed to the appearance of downstream travelling waves in the boundary layer that shed from the marginal separation zone and grow in size with either 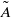$\tilde {A} $ or 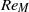$R{e}_{M} $. These unsteady, convective vortical structures relax the effect of the adverse pressure gradient on the viscous boundary layer to delay the onset of stall in the mean flow to higher values of 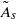${\tilde {A} }_{s} $. Computed results show agreement with marginal separation theory at low 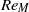$R{e}_{M} $ and with available experimental data at higher 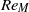$R{e}_{M} $. This simplified approach provides a universal criterion to determine the stall angle of stationary thin aerofoils with a parabolic nose.

A new method, herein referred to as optimal mode decomposition (OMD), of finding a linear model to describe the evolution of a fluid flow is presented. The method estimates the linear dynamics of a high-dimensional system which is first projected onto a subspace of a user-defined fixed rank. An iterative procedure is used to find the optimal combination of linear model and subspace that minimizes the system residual error. The OMD method is shown to be a generalization of dynamic mode decomposition (DMD), in which the subspace is not optimized but rather fixed to be the proper orthogonal decomposition (POD) modes. Furthermore, OMD is shown to provide an approximation to the Koopman modes and eigenvalues of the underlying system. A comparison between OMD and DMD is made using both a synthetic waveform and an experimental data set. The OMD technique is shown to have lower residual errors than DMD and is shown on a synthetic waveform to provide more accurate estimates of the system eigenvalues. This new method can be used with experimental and numerical data to calculate the ‘optimal’ low-order model with a user-defined rank that best captures the system dynamics of unsteady and turbulent flows.

We study small-amplitude axisymmetric shape oscillations of viscoelastic drops in a gas. The Jeffreys model is used as the rheological constitutive equation of the liquid, which represents a liquid with a frequency-dependent dynamic viscosity. The analysis of the time-dependent deformations caused by the oscillations yields the characteristic equation for the complex frequency, which describes the oscillation frequency and damping rate dependence on the viscous liquid behaviour and the stress relaxation and deformation retardation time scales ${\lambda }_{1} $ and ${\lambda }_{2} $ involved in the viscoelastic material law. The aim of this study is to quantify the influences of the two time scales on the oscillation behaviour of the drop and to propose an experimental method to determine one of the time scales by measuring damped oscillations of a drop. A proof-of-concept experiment is presented to show the potential and limitations of the method. Results show that values of ${\lambda }_{2} / {\lambda }_{1} $ from these measurements are orders of magnitude smaller than typical values used in simulations of viscoelastic flows.

A numerical study of swimming particle motion and nutrient transport is conducted for a semidilute to dense suspension in a thin film. The steady squirmer model is used to represent the motion of living cells in suspension with the nutrient uptake by swimming particles modelled using a first-order kinetic equation representing the absorption process that occurs locally at the particle surface. An analysis of the dynamics of the neutral squirmers inside the film shows that the vertical motion is reduced significantly. The mean nutrient uptake for both isolated and populations of swimmers decreases for increasing swimming speeds when nutrient advection becomes relevant as less time is left for the nutrient to diffuse to the surface. This finding is in contrast to the case where the uptake is modelled by imposing a constant nutrient concentration at the cell surface and the mass flux results to be an increasing monotonic function of the swimming speed. In comparison to non-motile particles, the cell motion has a negligible influence on nutrient uptake at lower particle absorption rates since the process is rate limited. At higher absorption rates, the swimming motion results in a large increase in the nutrient uptake that is attributed to the movement of particles and increased mixing in the fluid. As the volume fraction of swimming particles increases, the squirmers consume slightly less nutrients and require more power for the same swimming motion. Despite this increase in energy consumption, the results clearly demonstrate that the gain in nutrient uptake make swimming a winning strategy for micro-organism survival also in relatively dense suspensions.