Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-25T14:04:08.033Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological evolution in compressible turbulent boundary layers

Published online by Cambridge University Press:  23 September 2013

You-Biao Chu  and
Xi-Yun Lu
You-Biao Chu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, China
Xi-Yun Lu*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, China
*
†Email address for correspondence: xlu@ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

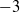Topological evolution of compressible turbulent boundary layers at Mach 2 is investigated by means of statistical analysis of the invariants of the velocity gradient tensor based on the direct numerical simulation database. The probability density functions of the rate of change of the invariants exhibit the $- 3$ power-law distribution in the region of large Lagrangian derivative of the invariants in the inner and outer layers. The topological evolution is studied by conditional mean trajectories for the evolution of the invariants. The trajectories illustrate inward-spiralling orbits around and converging to the origin of the space of invariants in the outer layer, while they are repelled by the vicinity of the origin and converge towards a limit cycle in the inner layer. The compressibility effect on the mean topological evolution is studied in terms of the ‘incompressible’, compressed and expanding regions. It is found that the mean evolution of flow topologies is altered by the compressibility. The evolution equations of the invariants are derived and the relevant dynamics of the mean topological evolution are analysed. The compressibility effect is mainly related to the pressure effect. The mutual-interaction terms among the invariants are the root of the clockwise spiral behaviour of the local flow topology in the space of invariants.

JFM classification

Compressible Flows: Compressible boundary layers Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 733 , 25 October 2013 , pp. 414 - 438
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreopoulos, Y. & Honkan, A. 2001 An experimental study of the dissipative and vortical motion in turbulent boundary layers. J. Fluid Mech. 439, 131–163.Google Scholar
Atkinson, C., Chumakov, S., Bermejo-Moreno, I. & Soria, J. 2012 Lagrangian evolution of the invariants of the velocity gradient tensor in a turbulent boundary layer. Phys. Fluids 24, 105104.Google Scholar
Atkinson, C., Coudert, S., Foucaut, J.-M., Stanislas, M. & Soria, J. 2011 The accuracy of tomographic particle image velocimetry for measurements of a turbulent boundary layer. Exp. Fluids 50, 1031–1056.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Mechanics. Cambridge University Press.Google Scholar
Bermejo-Moreno, I., Atkinson, C., Chumakov, S., Soria, J. & Wu, X. 2010 Flow topology and non-local geometry of structures in a flat-plate turbulent boundary layer. In Proceedings of the Summer Program. Centre for Turbulence Research, Stanford University.Google Scholar
Blackburn, H. M., Mansour, N. N. & Cantwell, B. J. 1996 Topology of fine-scale motions in turbulent channel flow. J. Fluid Mech. 310, 269–292.Google Scholar
Cantwell, B. J. 1992 Exact solution of a restricted Euler equation for the velocity gradient tensor. Phys. Fluids A 4 (4), 782–793.Google Scholar
Chacin, J. M. & Cantwell, B. J. 2000 Dynamics of a low Reynolds number turbulent boundary layer. J. Fluid Mech. 404, 87–115.Google Scholar
Chen, J. H., Chong, M. S., Soria, J., Sondergaard, R., Perry, A. E., Rogers, M., Moser, R. & Cantwell, B. J. 1990 A study of the topology of dissipating motions in direct numerical simulations of time-developing compressible and incompressible mixing layers. In Proceedings of the Summer Program. Centre for Turbulence Research, Stanford University.Google Scholar
Chertkov, M., Pumir, A. & Shraiman, B. I. 1999 Lagrangian tetrad dynamics and the phenomenology of turbulence. Phys. Fluids 11 (8), 2394–2410.Google Scholar
Chevillard, L. & Meneveau, C. 2006 Lagrangian dynamics and statistical geometric structure of turbulence. Phys. Rev. Lett. 97, 174501.Google Scholar
Chevillard, L., Meneveau, C., Biferale, L. & Toschi, F. 2008 Modelling the pressure Hessian and viscous Laplacian in turbulence: comparisons with direct numerical simulation and implications on velocity gradient dynamics. Phys. Fluids 20, 101504.Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2 (5), 765–777.Google Scholar
Chong, M. S., Soria, J., Perry, A. E., Chacin, J., Cantwell, B. J. & Na, Y. 1998 Turbulence structures of wall-bounded shear flows found using DNS data. J. Fluid Mech. 357, 225–247.Google Scholar
Chu, Y.-B. 2013 Numerical investigations of shock–shock interaction and supersonic turbulent boundary layer. PhD thesis, University of Science and Technology of China, Hefei.Google Scholar
Duan, L., Beekman, I. & Martín, M. P. 2011 Direct numerical simulation of hypersonic turbulent boundary layers. Part 3. Effect of Mach number. J. Fluid Mech. 672, 245–267.Google Scholar
Elsinga, G. E. & Marusic, I. 2010 Evolution and lifetimes of flow topology in a turbulent boundary layer. Phys. Fluids 22, 015102.Google Scholar
Frisch, U. 1995 Turbulence. Cambridge University Press.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2006 Large-scale motions in a supersonic turbulent boundary layer. J. Fluid Mech. 556, 271–282.Google Scholar
Girimaji, S. S. & Pope, S. B. 1990 A diffusion model for velocity gradients in turbulence. Phys. Fluids A 2 (2), 242–256.Google Scholar
Jeong, E. & Girimaji, S. S. 2003 Velocity-gradient dynamics in turbulence: effect of viscosity and forcing. Theor. Comput. Fluid Dyn. 16, 421–432.Google Scholar
Jiang, G. S. & Shu, C. W. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202–228.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Lagha, M., Kim, J., Eldredge, J. D. & Zhong, X. 2011 A numerical study of compressible turbulent boundary layers. Phys. Fluids 23, 015106.Google Scholar
Lee, K., Girimaji, S. S. & Kerimo, J. 2009 Effect of compressibility on turbulent velocity gradients and small-scale structure. J. Turbul. 10 (9), 1–18.Google Scholar
Li, Y., Chevillard, L., Eyink, G. & Meneveau, C. 2009 Matrix exponential-based closures for the turbulent subgrid-scale stress tensor. Phys. Rev. E 79, 016305.Google Scholar
Lüthi, B., Holzner, M. & Tsinober, A. 2009 Expanding the Q–R space to three dimensions. J. Fluid Mech. 641, 497–507.Google Scholar
Martín, J., Ooi, A., Chong, M. S. & Soria, J. 1998 Dynamics of the velocity gradient tensor invariants in isotropic turbulence. Phys. Fluids 10 (8), 2336–2346.Google Scholar
Martin, J., Ooi, A., Dopazo, C., Chong, M. S. & Soria, J. 1997 The inverse diffusion time scale of velocity gradients in homogeneous isotropic turbulence. Phys. Fluids 9 (4), 814–816.Google Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43, 219–245.Google Scholar
Mizuno, Y., Atkinson, C. & Soria, J. 2011 Topology and dynamics of flow structures in wall-bounded turbulent flows. J. Phys.: Conf. Ser. 318, 062018.Google Scholar
Ooi, A., Martin, J., Soria, J. & Chong, M. S. 1999 A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence. J. Fluid Mech. 381, 141–174.Google Scholar
Perry, A. E. & Chong, M. S. 1987 A description of eddying motions and flow patterns using critical-point concepts. Annu. Rev. Fluid Mech. 19, 125–155.Google Scholar
Pirozzoli, S., Bernardini, M. & Grasso, F. 2008 Characterization of coherent vortical structures in a supersonic turbulent boundary layer. J. Fluid Mech. 613, 205–231.Google Scholar
Pirozzoli, S. & Grasso, F. 2004 Direct numerical simulations of isotropic compressible turbulence: influence of compressibility on dynamics and structures. Phys. Fluids 16 (12), 4386–4407.Google Scholar
Pirozzoli, S., Grasso, F. & Gatski, T. B. 2004 Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer at $M= 2. 25$ . Phys. Fluids 16 (3), 530–545.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.Google Scholar
Shu, C. W. & Osher, S. 1988 Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77, 439–471.Google Scholar
Smits, A. J., Spina, E. F., Alving, A. E., Smith, R. W., Fernando, E. M. & Donovan, J. F. 1989 A comparison of the turbulence structure of subsonic and supersonic boundary layers. Phys. Fluids A 1 (11), 1865–1875.Google Scholar
Soria, J., Sondergaard, R., Cantwell, B. J., Chong, M. S. & Perry, A. E. 1994 A study of the fine-scale motions of incompressible time-developing mixing layers. Phys. Fluids 6 (2), 871–884.Google Scholar
Suman, S. & Girimaji, S. S. 2009 Homogenized Euler equation: a model for compressible velocity gradient dynamics. J. Fluid Mech. 620, 177–194.Google Scholar
Suman, S. & Girimaji, S. S. 2010 Velocity gradient invariants and local flow field topology in compressible turbulence. J. Turbul. 11 (2), 1–24.Google Scholar
Suman, S. & Girimaji, S. S. 2012 Velocity-gradient dynamics in compressible turbulence: influence of Mach number and dilatation rate. J. Turbul. 13 (8), 1–23.Google Scholar
Taylor, G. I. 1938 Production and dissipation of vorticity in a turbulent fluid. Proc. R. Soc. Lond. A 164, 15–23.Google Scholar
Tsinober, A. 2000 Vortex stretching versus production of strain/dissipation. In Turbulence Structure and Vortex Dynamics, pp. 164–191. Cambridge University Press.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence. Springer.Google Scholar
van der Bos, F., Tao, B., Meneveau, C. & Katz, J. 2002 Effects of small-scale turbulent motions on the filtered velocity gradient tensor as deduced from holographic particle image velocimetry measurements. Phys. Fluids 14 (7), 2456–2474.Google Scholar
Vieillefosse, P. 1982 Local interaction between vorticity and shear in a perfect incompressible fluid. J. Phys. Paris 43, 837–842.Google Scholar
Wang, B.-C., Bergstrom, D. J., Yin, J. & Yee, E. 2006 Turbulence topologies predicted using large eddy simulations. J. Turbul. 7 (34), 1–28.Google Scholar
Wang, J., Shi, Y., Wang, L.-P., Xiao, Z., He, X. T. & Chen, S. 2012 Effect of compressibility on the small-scale structures in isotropic turbulence. J. Fluid Mech. 713, 588–631.Google Scholar
Wang, L. & Lu, X.-Y. 2012 Flow topology in compressible turbulent boundary layer. J. Fluid Mech. 703, 255–278.Google Scholar
Wu, X. & Moin, P. 2010 Transitional and turbulent boundary layer with heat transfer. Phys. Fluids 22, 085105.Google Scholar