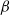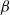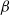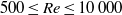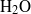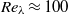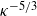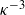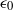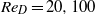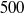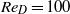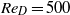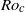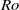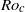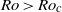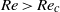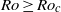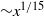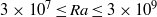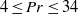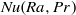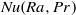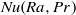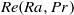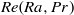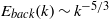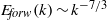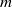Focus on Fluids
Multiphase flow in porous media
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 1-4
-
- Article
-
- You have access
- Export citation
Papers
Three-dimensional instability of the flow around a rotating circular cylinder
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 5-18
-
- Article
- Export citation
Unsteady separation leading to secondary and tertiary vortex dynamics: the sub-
 $\alpha $- and sub-
$\alpha $- and sub-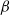 $\beta $-phenomena
$\beta $-phenomena
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 19-51
-
- Article
- Export citation
Relationship between aerodynamic forces, flow structures and wing camber for rotating insect wing planforms
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 52-75
-
- Article
- Export citation
Grid turbulence in dilute polymer solutions: PEO in water
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 76-98
-
- Article
- Export citation
Experiments on an elliptic circulation control aerofoil
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 99-144
-
- Article
- Export citation
The drag-adjoint field of a circular cylinder wake at Reynolds numbers 20, 100 and 500
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 145-161
-
- Article
- Export citation
Wake states and frequency selection of a streamwise oscillating cylinder
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 162-192
-
- Article
- Export citation
Laminarization mechanisms and extreme-amplitude states in rapidly rotating plane channel flow
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 193-219
-
- Article
- Export citation
Two-scale dynamics of flow past a partial cross-stream array of tidal turbines
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 220-244
-
- Article
- Export citation
Ultrasonic cavitation near a tissue layer
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 245-272
-
- Article
- Export citation
Comparison between spatial and temporal wall oscillations in turbulent boundary layer flows
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 273-294
-
- Article
- Export citation
The unifying theory of scaling in thermal convection: the updated prefactors
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 295-308
-
- Article
- Export citation
Split energy–helicity cascades in three-dimensional homogeneous and isotropic turbulence
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 309-327
-
- Article
- Export citation
Drop impact on super-wettability-contrast annular patterns
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 328-342
-
- Article
- Export citation
Interfacial instability of coupled-rotating inviscid fluids
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 343-363
-
- Article
- Export citation
Instability of an inviscid flow between porous cylinders with radial flow
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 364-378
-
- Article
- Export citation
Three-dimensionality in the wake of a rapidly rotating cylinder in uniform flow
-
- Published online by Cambridge University Press:
- 30 July 2013, pp. 379-391
-
- Article
- Export citation
Unsteady three-dimensional sources in deep water with an elastic cover and their applications
-
- Published online by Cambridge University Press:
- 01 August 2013, pp. 392-418
-
- Article
- Export citation
Instabilities of the flow around a cylinder and emission of vortex dipoles
-
- Published online by Cambridge University Press:
- 01 August 2013, pp. 419-441
-
- Article
- Export citation