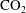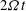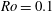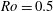Focus on Fluids
A decade’s investigation of the stability of erodible stream beds
-
- Published online by Cambridge University Press:
- 03 September 2014, pp. 1-4
-
- Article
-
- You have access
- Export citation
Papers
Fluid flow analysis of a shark-inspired microstructure
-
- Published online by Cambridge University Press:
- 01 September 2014, pp. 5-29
-
- Article
- Export citation
Space–time characteristics of a compliant wall in a turbulent channel flow
-
- Published online by Cambridge University Press:
- 01 September 2014, pp. 30-53
-
- Article
- Export citation
Segregation in dense sheared flows: gravity, temperature gradients, and stress partitioning
-
- Published online by Cambridge University Press:
- 01 September 2014, pp. 54-88
-
- Article
- Export citation
Heat transport and pressure buildup during carbon dioxide injection into depleted gas reservoirs
-
- Published online by Cambridge University Press:
- 01 September 2014, pp. 89-109
-
- Article
-
- You have access
- Open access
- Export citation
Confinement effects in wind-turbine and propeller measurements
-
- Published online by Cambridge University Press:
- 01 September 2014, pp. 110-129
-
- Article
- Export citation
The effectiveness of an air curtain in the doorway of a ventilated building
-
- Published online by Cambridge University Press:
- 01 September 2014, pp. 130-164
-
- Article
- Export citation
Interference effects of three consecutive wall-mounted cubes placed in deep turbulent boundary layer
-
- Published online by Cambridge University Press:
- 01 September 2014, pp. 165-190
-
- Article
- Export citation
Pressure Hessian and viscous contributions to velocity gradient statistics based on Gaussian random fields
-
- Published online by Cambridge University Press:
- 01 September 2014, pp. 191-225
-
- Article
-
- You have access
- Export citation
Longitudinal–transverse aerodynamic force in viscous compressible complex flow
-
- Published online by Cambridge University Press:
- 01 September 2014, pp. 226-251
-
- Article
- Export citation
Evolution of the velocity-gradient tensor in a spatially developing turbulent flow
-
- Published online by Cambridge University Press:
- 01 September 2014, pp. 252-292
-
- Article
- Export citation
Resonance patterns in spatially forced Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 01 September 2014, pp. 293-308
-
- Article
- Export citation
Wave turbulence in the two-layer ocean model
-
- Published online by Cambridge University Press:
- 01 September 2014, pp. 309-327
-
- Article
- Export citation
Shock wave–boundary layer interactions in rectangular inlets: three-dimensional separation topology and critical points
-
- Published online by Cambridge University Press:
- 02 September 2014, pp. 328-353
-
- Article
- Export citation
Flow structure on a simultaneously pitching and rotating wing
-
- Published online by Cambridge University Press:
- 02 September 2014, pp. 354-383
-
- Article
- Export citation
Pressure fluctuations produced by forward steps immersed in a turbulent boundary layer
-
- Published online by Cambridge University Press:
- 02 September 2014, pp. 384-421
-
- Article
- Export citation
Numerical investigation of tandem-cylinder noise reduction using plasma-based flow control
-
- Published online by Cambridge University Press:
- 02 September 2014, pp. 422-451
-
- Article
- Export citation
Three-dimensional boundary layers with short spanwise scales
-
- Published online by Cambridge University Press:
- 02 September 2014, pp. 452-469
-
- Article
- Export citation
Intermittency route to thermoacoustic instability in turbulent combustors
-
- Published online by Cambridge University Press:
- 02 September 2014, pp. 470-487
-
- Article
- Export citation
Evolution of a turbulent cloud under rotation
-
- Published online by Cambridge University Press:
- 02 September 2014, pp. 488-509
-
- Article
- Export citation