Article contents
Heat transport and pressure buildup during carbon dioxide injection into depleted gas reservoirs
Published online by Cambridge University Press: 01 September 2014
Abstract
In this article, a two-layer vertical equilibrium model for the injection of carbon dioxide into a low-pressure porous reservoir containing methane and water is developed. The dependent variables solved for include pressure, temperature and 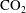 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathrm{CO}}_2$–
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathrm{CO}}_2$–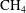 ${\mathrm{CH}}_4$ interface height. In contrast to previous two-layer vertical equilibrium models in this context, the compressibility of all material components is fully accounted for. Non-Darcy effects are also considered using the Forchheimer equation. The results show that, for a given injection scenario, as the initial pressure in the reservoir decreases, both the pressure buildup and temperature change increase. A comparison was conducted between a fully coupled non-isothermal numerical model and a simplified model where fluid properties are held constant with temperature. This simplified model was found to provide an excellent approximation when using the injection fluid temperature for calculating fluid properties, even when the injection fluid was as much as
${\mathrm{CH}}_4$ interface height. In contrast to previous two-layer vertical equilibrium models in this context, the compressibility of all material components is fully accounted for. Non-Darcy effects are also considered using the Forchheimer equation. The results show that, for a given injection scenario, as the initial pressure in the reservoir decreases, both the pressure buildup and temperature change increase. A comparison was conducted between a fully coupled non-isothermal numerical model and a simplified model where fluid properties are held constant with temperature. This simplified model was found to provide an excellent approximation when using the injection fluid temperature for calculating fluid properties, even when the injection fluid was as much as 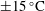 $\pm 15\, ^\circ \mathrm{C}$ of the initial reservoir temperature. The implications are that isothermal models can be expected to provide useful estimates of pressure buildup in this context. Despite the low viscosity of
$\pm 15\, ^\circ \mathrm{C}$ of the initial reservoir temperature. The implications are that isothermal models can be expected to provide useful estimates of pressure buildup in this context. Despite the low viscosity of 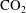 ${\mathrm{CO}}_2$ at the low pressures studied, non-Darcy effects were found to be of negligible concern throughout the sensitivity analysis undertaken. This is because the
${\mathrm{CO}}_2$ at the low pressures studied, non-Darcy effects were found to be of negligible concern throughout the sensitivity analysis undertaken. This is because the 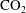 ${\mathrm{CO}}_2$ density is also low in this context. Based on these findings, simplified analytic solutions are derived, which accurately calculate both the pressure buildup and temperature decline during the injection period.
${\mathrm{CO}}_2$ density is also low in this context. Based on these findings, simplified analytic solutions are derived, which accurately calculate both the pressure buildup and temperature decline during the injection period.
- Type
- Papers
- Information
- Creative Commons
- The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
- Copyright
- © 2014 Cambridge University Press
References
- 18
- Cited by


