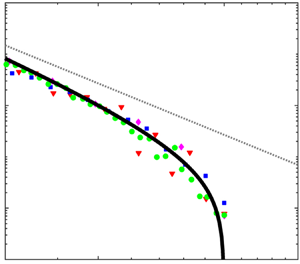
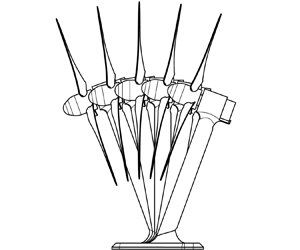
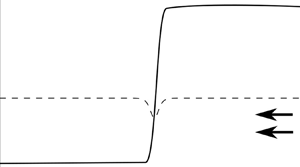
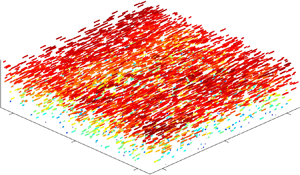
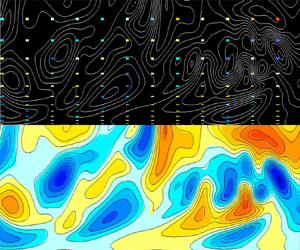
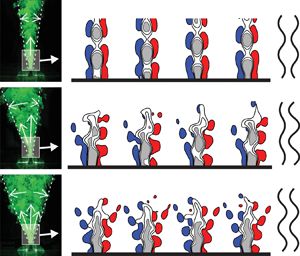
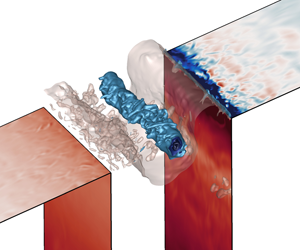
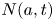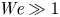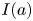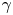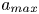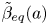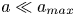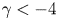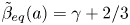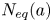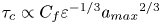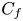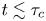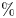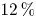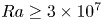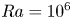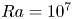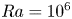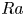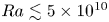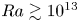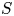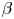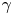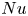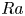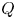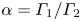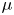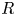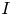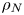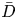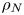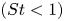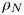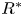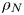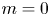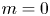Graphical abstract from Sivasankar, V., Etha, S., Sachar, H. & Das, S. 2021 Thermo-osmotic transport in nanochannels grafted with pH-responsive polyelectrolyte brushes modelled using augmented strong stretching theory. J. Fluid Mech. 917, A31. doi:10.1017/jfm.2021.281.
JFM Rapids
Effects of power-law entrainment on bubble fragmentation cascades
-
- Published online by Cambridge University Press:
- 28 April 2021, R1
-
- Article
- Export citation
JFM Papers
Turbulent boundary-layer flow over regular multiscale roughness
-
- Published online by Cambridge University Press:
- 21 April 2021, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dilute dispersion of compound particles: deformation dynamics and rheology
-
- Published online by Cambridge University Press:
- 21 April 2021, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantification of wake shape modulation and deflection for tilt and yaw misaligned wind turbines
-
- Published online by Cambridge University Press:
- 21 April 2021, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hydraulic control of continental shelf waves
-
- Published online by Cambridge University Press:
- 21 April 2021, A4
-
- Article
- Export citation
Low-order models for predicting radiative transfer effects on Rayleigh–Bénard convection in a cubic cell at different Rayleigh numbers
-
- Published online by Cambridge University Press:
- 21 April 2021, A5
-
- Article
- Export citation
Regime transitions in thermally driven high-Rayleigh number vertical convection
-
- Published online by Cambridge University Press:
- 21 April 2021, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A direct comparison of turbulence in drag-reduced flows of polymers and surfactants
-
- Published online by Cambridge University Press:
- 21 April 2021, A7
-
- Article
- Export citation
Time-resolved wake dynamics of finite wall-mounted circular cylinders submerged in a turbulent boundary layer
-
- Published online by Cambridge University Press:
- 21 April 2021, A8
-
- Article
- Export citation
State estimation in turbulent channel flow from limited observations
-
- Published online by Cambridge University Press:
- 22 April 2021, A9
-
- Article
- Export citation
Peristaltic pumping in thin non-axisymmetric annular tubes
-
- Published online by Cambridge University Press:
- 23 April 2021, A10
-
- Article
- Export citation
Topological bifurcations of vortex pair interactions
-
- Published online by Cambridge University Press:
- 23 April 2021, A11
-
- Article
- Export citation
Experimental study of the effects of droplet number density on turbulence-driven polydisperse droplet size growth
-
- Published online by Cambridge University Press:
- 23 April 2021, A12
-
- Article
- Export citation
Flow and residence time in a two-dimensional aquifer recharged by rainfall
-
- Published online by Cambridge University Press:
- 23 April 2021, A13
-
- Article
- Export citation
Stability and dynamics of convection in dry salt lakes
-
- Published online by Cambridge University Press:
- 23 April 2021, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Magnetofluidic mixing of a ferrofluid droplet under the influence of a time-dependent external field
-
- Published online by Cambridge University Press:
- 23 April 2021, A15
-
- Article
- Export citation
The response of an axisymmetric jet placed at various positions in a standing wave
-
- Published online by Cambridge University Press:
- 23 April 2021, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A wall-resolved large-eddy simulation of deep cavity flow in acoustic resonance
-
- Published online by Cambridge University Press:
- 23 April 2021, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sparsity-promoting algorithms for the discovery of informative Koopman-invariant subspaces
-
- Published online by Cambridge University Press:
- 26 April 2021, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interactions of waves with a body floating in an open water channel confined by two semi-infinite ice sheets
-
- Published online by Cambridge University Press:
- 23 April 2021, A19
-
- Article
- Export citation