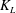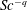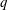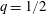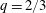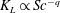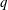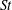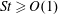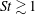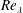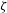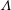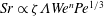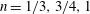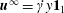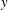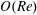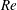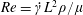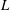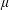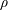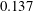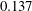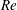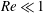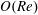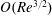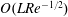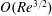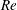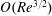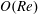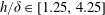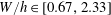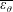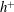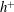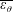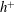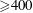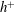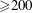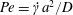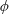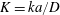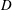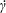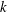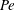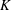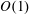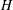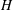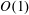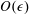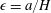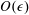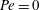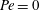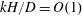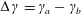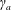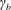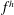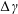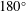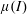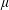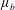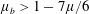We calculate the leading-order correction to the time period of rotation of a neutrally buoyant spheroid of arbitrary aspect ratio, in a simple shear flow (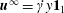 $\boldsymbol{u}^{\infty }=\dot{\unicode[STIX]{x1D6FE}}y\mathbf{1}_{1}$;
$\boldsymbol{u}^{\infty }=\dot{\unicode[STIX]{x1D6FE}}y\mathbf{1}_{1}$;  $\mathbf{1}_{1}$ is the unit vector in the flow direction,
$\mathbf{1}_{1}$ is the unit vector in the flow direction, 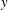 $y$ being the coordinate along the gradient direction), in its long-time orbit set up by the weak fluid inertial drift at
$y$ being the coordinate along the gradient direction), in its long-time orbit set up by the weak fluid inertial drift at 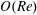 $O(Re)$. Here,
$O(Re)$. Here, 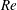 $Re$ is the microscale Reynolds number, a dimensionless measure of the fluid inertial effects on the length scale of the spheroid, and is defined as
$Re$ is the microscale Reynolds number, a dimensionless measure of the fluid inertial effects on the length scale of the spheroid, and is defined as 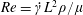 $Re=\dot{\unicode[STIX]{x1D6FE}}L^{2}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D707}$, where
$Re=\dot{\unicode[STIX]{x1D6FE}}L^{2}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D707}$, where 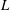 $L$ is the semimajor axis of the spheroid,
$L$ is the semimajor axis of the spheroid, 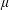 $\unicode[STIX]{x1D707}$ and
$\unicode[STIX]{x1D707}$ and 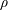 $\unicode[STIX]{x1D70C}$ are respectively the viscosity and density of the fluid, and
$\unicode[STIX]{x1D70C}$ are respectively the viscosity and density of the fluid, and  $\dot{\unicode[STIX]{x1D6FE}}$ is the shear rate. This long-time orbit is the tumbling orbit for prolate spheroids; for oblate spheroids, it is the spinning orbit for aspect ratios greater than
$\dot{\unicode[STIX]{x1D6FE}}$ is the shear rate. This long-time orbit is the tumbling orbit for prolate spheroids; for oblate spheroids, it is the spinning orbit for aspect ratios greater than 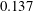 $0.137$, and can be either the tumbling or the spinning orbit for oblate spheroids of aspect ratios less than
$0.137$, and can be either the tumbling or the spinning orbit for oblate spheroids of aspect ratios less than 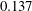 $0.137$. We also calculate the leading-order correction to the time period of rotation of a neutrally buoyant triaxial ellipsoid in a simple shear flow, rotating with its intermediate principal axis aligned along the vorticity of the flow; the latter calculation is in light of recent evidence, by way of numerical simulations (Rosen, PhD dissertation, 2016, Stockholm), of the aforementioned rotation being stabilized by weak inertia. The correction to the time period for arbitrary
$0.137$. We also calculate the leading-order correction to the time period of rotation of a neutrally buoyant triaxial ellipsoid in a simple shear flow, rotating with its intermediate principal axis aligned along the vorticity of the flow; the latter calculation is in light of recent evidence, by way of numerical simulations (Rosen, PhD dissertation, 2016, Stockholm), of the aforementioned rotation being stabilized by weak inertia. The correction to the time period for arbitrary 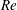 $Re$ is expressed as a volume integral using a generalized reciprocal theorem formulation. For
$Re$ is expressed as a volume integral using a generalized reciprocal theorem formulation. For 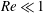 $Re\ll 1$, it is shown that the correction at
$Re\ll 1$, it is shown that the correction at 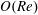 $O(Re)$ is zero for spheroids (with aspect ratios of order unity) as well as triaxial ellipsoids in their long-time orbits. The first correction to the time period therefore occurs at
$O(Re)$ is zero for spheroids (with aspect ratios of order unity) as well as triaxial ellipsoids in their long-time orbits. The first correction to the time period therefore occurs at 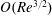 $O(Re^{3/2})$, and has a singular origin, arising from fluid inertial effects in the outer region (distances from the spheroid or triaxial ellipsoid of the order of the inertial screening length of
$O(Re^{3/2})$, and has a singular origin, arising from fluid inertial effects in the outer region (distances from the spheroid or triaxial ellipsoid of the order of the inertial screening length of 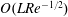 $O(LRe^{-1/2})$), where the leading-order Stokes approximation ceases to be valid. Since the correction comes from the effects of inertia in the far field, the rotating spheroid (triaxial ellipsoid) is approximated as a time-dependent point-force-dipole singularity, allowing for the reciprocal theorem integral to be evaluated in Fourier space. It is shown for all relevant cases that fluid inertia at
$O(LRe^{-1/2})$), where the leading-order Stokes approximation ceases to be valid. Since the correction comes from the effects of inertia in the far field, the rotating spheroid (triaxial ellipsoid) is approximated as a time-dependent point-force-dipole singularity, allowing for the reciprocal theorem integral to be evaluated in Fourier space. It is shown for all relevant cases that fluid inertia at 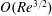 $O(Re^{3/2})$ leads to an increase in the time period of rotation compared with that in the Stokes limit, consistent with the results of recent numerical simulations at finite
$O(Re^{3/2})$ leads to an increase in the time period of rotation compared with that in the Stokes limit, consistent with the results of recent numerical simulations at finite 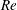 $Re$. Finally, combination of the
$Re$. Finally, combination of the 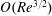 $O(Re^{3/2})$ correction derived here with the
$O(Re^{3/2})$ correction derived here with the 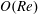 $O(Re)$ correction derived earlier by Dabade et al. (J. Fluid Mech., vol. 791, 2016, 631703) yields a uniformly valid description of the first effects of inertia for spheroids of all aspect ratios, including prediction of the arrest of rotation for extreme-aspect-ratio spheroids.
$O(Re)$ correction derived earlier by Dabade et al. (J. Fluid Mech., vol. 791, 2016, 631703) yields a uniformly valid description of the first effects of inertia for spheroids of all aspect ratios, including prediction of the arrest of rotation for extreme-aspect-ratio spheroids.