We report an investigation of inverse energy cascade in steady-state two-dimensional turbulence by direct numerical simulation (DNS) of the two-dimensional Navier–Stokes equation, with small-scale forcing and large-scale damping. We employed several types of damping and dissipation mechanisms in simulations up to 20482 resolution. For all these simulations we obtained a wavenumber range for which the mean spectral energy flux is a negative constant and the energy spectrum scales as k−5/3, consistent with the predictions of Kraichnan (Phys. Fluids, vol. 439, 1967, p. 1417). To gain further insight, we investigated the energy cascade in physical space, employing a local energy flux defined by smooth filtering. We found that the inverse energy cascade is scale local, but that the strongly local contribution vanishes identically, as argued by Kraichnan (J. Fluid Mech., vol. 47, 1971, p. 525). The mean flux across a length scale ℓ was shown to be due mainly to interactions with modes two to eight times smaller. A major part of our investigation was devoted to identifying the physical mechanism of the two-dimensional inverse energy cascade. One popular idea is that inverse energy cascade proceeds via merger of like-sign vortices. We made a quantitative study employing a precise topological criterion of merger events. Our statistical analysis showed that vortex mergers play a negligible direct role in producing mean inverse energy flux in our simulations. Instead, we obtained with the help of other works considerable evidence in favour of a ‘vortex thinning’ mechanism, according to which the large-scale strains do negative work against turbulent stress as they stretch out the isolines of small-scale vorticity. In particular, we studied a multi-scale gradient (MSG) expansion developed by Eyink (J. Fluid Mech., vol. 549, 2006a, p. 159) for the turbulent stress, whose contributions to inverse cascade can all be explained by ‘thinning’. The MSG expansion up to second order in space gradients was found to predict well the magnitude, spatial structure and scale distribution of the local energy flux. The majority of mean flux was found to be due to the relative rotation of strain matrices at different length scales, a first-order effect of ‘thinning’. The remainder arose from two second-order effects, differential strain rotation and vorticity gradient stretching. Our findings give strong support to vortex thinning as the fundamental mechanism of two-dimensional inverse energy cascade.




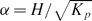 . For α ≪ 1 the solutions for both cases approach the classical solution for a slider bearing. For α ≫ 1 we show, using asymptotic analysis that the solutions diverge dramatically. In case (
. For α ≪ 1 the solutions for both cases approach the classical solution for a slider bearing. For α ≫ 1 we show, using asymptotic analysis that the solutions diverge dramatically. In case (