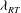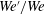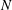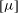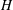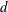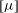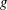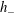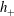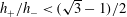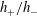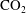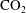Focus on Fluids
Challenging the large eddy simulation technique with advanced a posteriori tests
-
- Published online by Cambridge University Press:
- 23 December 2014, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
The motion of a 2D pendulum in a channel subjected to an incoming flow
-
- Published online by Cambridge University Press:
- 22 December 2014, pp. 5-25
-
- Article
- Export citation
A multilayer ice-flow model generalising the shallow shelf approximation
-
- Published online by Cambridge University Press:
- 22 December 2014, pp. 26-51
-
- Article
- Export citation
Stirring and scalar transfer by grid-generated turbulence in the presence of a mean scalar gradient
-
- Published online by Cambridge University Press:
- 23 December 2014, pp. 52-75
-
- Article
- Export citation
Thin-film flow in helically-wound rectangular channels of arbitrary torsion and curvature
-
- Published online by Cambridge University Press:
- 23 December 2014, pp. 76-94
-
- Article
- Export citation
Air-assisted atomization of liquid jets in varying levels of turbulence
-
- Published online by Cambridge University Press:
- 23 December 2014, pp. 95-132
-
- Article
- Export citation
High-frequency viscosity of a dilute suspension of elongated particles in a linear shear flow between two walls
-
- Published online by Cambridge University Press:
- 23 December 2014, pp. 133-147
-
- Article
- Export citation
Flows produced by the combined oscillatory rotation and translation of a circular cylinder in a quiescent fluid
-
- Published online by Cambridge University Press:
- 23 December 2014, pp. 148-170
-
- Article
- Export citation
Long-range wall perturbations in dense granular flows
-
- Published online by Cambridge University Press:
- 23 December 2014, pp. 171-192
-
- Article
- Export citation
The linear stability of a Stokes layer subjected to high-frequency perturbations
-
- Published online by Cambridge University Press:
- 23 December 2014, pp. 193-218
-
- Article
- Export citation
A scaling analysis of transient natural convection in a reservoir model induced by iso-flux heating
-
- Published online by Cambridge University Press:
- 23 December 2014, pp. 219-249
-
- Article
- Export citation
Spatio-temporal structure of the ‘fully developed’ transitional flow in a symmetric wavy channel. Linear and weakly nonlinear stability analysis
-
- Published online by Cambridge University Press:
- 29 December 2014, pp. 250-276
-
- Article
- Export citation
An example where lubrication theory comes short: hydraulic jumps in a flow down an inclined plate
-
- Published online by Cambridge University Press:
- 29 December 2014, pp. 277-295
-
- Article
- Export citation
Rock dissolution patterns and geochemical shutdown of
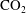 $\text{CO}_{2}$–brine–carbonate reactions during convective mixing in porous media
$\text{CO}_{2}$–brine–carbonate reactions during convective mixing in porous media
-
- Published online by Cambridge University Press:
- 05 January 2015, pp. 296-315
-
- Article
- Export citation
Thermomagnetic convection in a layer of ferrofluid placed in a uniform oblique external magnetic field
-
- Published online by Cambridge University Press:
- 05 January 2015, pp. 316-348
-
- Article
- Export citation
Vertical natural convection: application of the unifying theory of thermal convection
-
- Published online by Cambridge University Press:
- 06 January 2015, pp. 349-361
-
- Article
- Export citation
Direct numerical simulation of a turbulent jet impinging on a heated wall
-
- Published online by Cambridge University Press:
- 05 January 2015, pp. 362-394
-
- Article
- Export citation
Transition of transient channel flow after a change in Reynolds number
-
- Published online by Cambridge University Press:
- 05 January 2015, pp. 395-427
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free radially expanding liquid sheet in air: time- and space-resolved measurement of the thickness field
-
- Published online by Cambridge University Press:
- 08 January 2015, pp. 428-444
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The asymptotics of the moving contact line: cracking an old nut
-
- Published online by Cambridge University Press:
- 08 January 2015, pp. 445-462
-
- Article
- Export citation