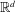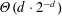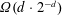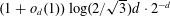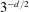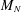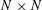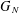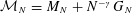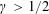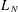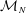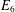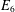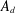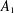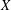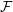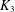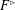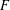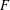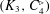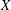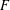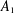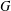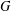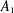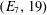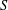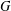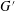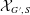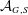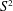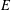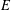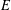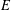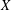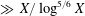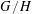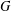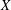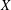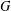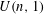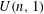Discrete Mathematics
Research Article
ON THE HARD SPHERE MODEL AND SPHERE PACKINGS IN HIGH DIMENSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 14 January 2019, e1
-
- Article
-
- You have access
- Open access
- Export citation
Foundations
Research Article
MONOID ACTIONS AND ULTRAFILTER METHODS IN RAMSEY THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2019, e2
-
- Article
-
- You have access
- Open access
- Export citation
Analysis
Research Article
REGULARIZATION OF NON-NORMAL MATRICES BY GAUSSIAN NOISE—THE BANDED TOEPLITZ AND TWISTED TOEPLITZ CASES
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2019, e3
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
COMPATIBLE SYSTEMS OF GALOIS REPRESENTATIONS ASSOCIATED TO THE EXCEPTIONAL GROUP
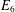 $E_{6}$
$E_{6}$
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2019, e4
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
Research Article
GL-EQUIVARIANT MODULES OVER POLYNOMIAL RINGS IN INFINITELY MANY VARIABLES. II
-
- Published online by Cambridge University Press:
- 12 March 2019, e5
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Research Article
OBSTRUCTIONS TO ALGEBRAIZING TOPOLOGICAL VECTOR BUNDLES
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2019, e6
-
- Article
-
- You have access
- Open access
- Export citation
Mathematical Physics
Research Article
DONALDSON–THOMAS INVARIANTS OF LOCAL ELLIPTIC SURFACES VIA THE TOPOLOGICAL VERTEX
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2019, e7
-
- Article
-
- You have access
- Open access
- Export citation
Probability
Research Article
RANDOM MATRICES WITH SLOW CORRELATION DECAY
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2019, e8
-
- Article
-
- You have access
- Open access
- Export citation
Discrete Mathematics
Research Article
FORCING QUASIRANDOMNESS WITH TRIANGLES
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2019, e9
-
- Article
-
- You have access
- Open access
- Export citation
Computational Mathematics
Research Article
VARIETIES OF SIGNATURE TENSORS
- Part of:
-
- Published online by Cambridge University Press:
- 04 April 2019, e10
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Research Article
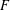 $F$-SIGNATURE UNDER BIRATIONAL MORPHISMS
$F$-SIGNATURE UNDER BIRATIONAL MORPHISMS
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2019, e11
-
- Article
-
- You have access
- Open access
- Export citation
Algebra
Research Article
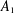 $A_{1}$-TYPE SUBGROUPS CONTAINING REGULAR UNIPOTENT ELEMENTS
$A_{1}$-TYPE SUBGROUPS CONTAINING REGULAR UNIPOTENT ELEMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2019, e12
-
- Article
-
- You have access
- Open access
- Export citation
Mathematical Physics
Research Article
CLUSTER STRUCTURES ON HIGHER TEICHMULLER SPACES FOR CLASSICAL GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 08 May 2019, e13
-
- Article
-
- You have access
- Open access
- Export citation
Topology
Research Article
SIMPLY CONNECTED, SPINELESS 4-MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2019, e14
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
GOLDFELD’S CONJECTURE AND CONGRUENCES BETWEEN HEEGNER POINTS
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2019, e15
-
- Article
-
- You have access
- Open access
- Export citation
ENLARGED MIXED SHIMURA VARIETIES, BI-ALGEBRAIC SYSTEM AND SOME AX TYPE TRANSCENDENTAL RESULTS
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2019, e16
-
- Article
-
- You have access
- Open access
- Export citation
A PROOF OF ANDREWS’ CONJECTURE ON PARTITIONS WITH NO SHORT SEQUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2019, e17
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic and Complex Geometry
Research Article
A FILTRATION ON EQUIVARIANT BOREL–MOORE HOMOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 04 July 2019, e18
-
- Article
-
- You have access
- Open access
- Export citation
Number Theory
Research Article
ENDOSCOPY AND COHOMOLOGY IN A TOWER OF CONGRUENCE MANIFOLDS FOR
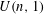 $U(n,1)$
$U(n,1)$
- Part of:
-
- Published online by Cambridge University Press:
- 15 July 2019, e19
-
- Article
-
- You have access
- Open access
- Export citation
DEFORMATION CONDITIONS FOR PSEUDOREPRESENTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 18 July 2019, e20
-
- Article
-
- You have access
- Open access
- Export citation