Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-26T00:46:49.527Z Has data issue: false hasContentIssue false
  • English
  • Français

ENDOSCOPY AND COHOMOLOGY IN A TOWER OF CONGRUENCE MANIFOLDS FOR 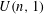$U(n,1)$

Part of: Complex spaces with a group of automorphisms Automorphic functions

Published online by Cambridge University Press:  15 July 2019

SIMON MARSHALL Open the ORCID record for SIMON MARSHALL [Opens in a new window]  and
SUG WOO SHIN
SIMON MARSHALL
Affiliation:
Department of Mathematics, University of Wisconsin – Madison, 480 Lincoln Drive, Madison, WI 53706, USA; marshall@math.wisc.edu
SUG WOO SHIN
Affiliation:
Department of Mathematics, University of California, Berkeley, 901 Evans Hall, Berkeley, CA 94720, USA; sug.woo.shin@berkeley.edu Korea Institute for Advanced Study, Dongdaemun-gu, Seoul 130-722, Republic of Korea

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By assuming the endoscopic classification of automorphic representations on inner forms of unitary groups, which is currently work in progress by Kaletha, Minguez, Shin, and White, we bound the growth of cohomology in congruence towers of locally symmetric spaces associated to 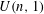$U(n,1)$. In the case of lattices arising from Hermitian forms, we expect that the growth exponents we obtain are sharp in all degrees.

MSC classification

Primary: 32N10: Automorphic forms
Secondary: 32M15: Hermitian symmetric spaces, bounded symmetric domains, Jordan algebras
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e19
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Arthur, J., The Endoscopic Classification of Representations, American Mathematical Society Colloquium Publications, 61 (American Mathematical Society, Providence, RI, 2013).Google Scholar
Bergeron, N. and Clozel, L., ‘Spectre automorphe des variétés hyperboliques et applications topologiques’, Astérisque 303 (2005), xx+218.Google Scholar
Bergeron, N., Millson, J. and Moeglin, C., ‘The Hodge conjecture and arithmetic quotients of complex balls’, Acta Math. 216(1) (2016), 1–125.Google Scholar
Bernstein, J. N., ‘Le “centre” de Bernstein’, inRepresentations of Reductive Groups Over a Local Field, Travaux en Cours (ed. Deligne, P.) (Hermann, Paris, 1984), 1–32.Google Scholar
Bernšteĭn, I. N., ‘All reductive p-adic groups are of type I’, Funkcional. Anal. i Priložen. 8(2) (1974), 3–6.Google Scholar
Borel, A. and Wallach, N., Continuous cohomology, discrete subgroups, and representations of reductive groups, 2nd edn, Mathematical Surveys and Monographs, 67 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Bushnell, C. J. and Kutzko, P. C., The Admissible Dual of  GL(N) via Compact Open Subgroups, Annals of Mathematics Studies, 129 (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Buzzard, K. and Gee, T., ‘The conjectural connections between automorphic representations and Galois representations’, inAutomorphic Forms and Galois Representations, Vol. 1, London Mathematical Society Lecture Note Series, 414 (Cambridge University Press, Cambridge, 2014), 135–187.Google Scholar
Caraiani, A., ‘Local-global compatibility and the action of monodromy on nearby cycles’, Duke Math. J. 161(12) (2012), 2311–2413.Google Scholar
Carayol, H., ‘Représentations cuspidales du groupe linéaire’, Ann. Sci. Éc. Norm. Supér. (4) 17(2) (1984), 191–225.Google Scholar
Clozel, L., ‘Motifs et formes automorphes: applications du principe de fonctorialité’, inAutomorphic Forms, Shimura Varieties, and L-Functions, Vol. I (Ann Arbor, MI, 1988), Perspectives on Mathematics, 10 (Academic Press, Boston, MA, 1990), 77–159.Google Scholar
Cossutta, M. and Marshall, S., ‘Theta lifting and cohomology growth in p-adic towers’, Int. Math. Res. Not. IMRN 2013(11) (2013), 2601–2623.Google Scholar
de George, D. L. and Wallach, N. R., ‘Limit formulas for multiplicities in L 2(𝛤\G)’, Ann. of Math. (2) 107(1) (1978), 133–150.Google Scholar
Gelbart, S. S., Automorphic forms on adèle groups, Annals of Mathematics Studies, No. 83 (Princeton University Press, Princeton, NJ, 1975), University of Tokyo Press, Tokyo.Google Scholar
Howe, R. E., ‘Tamely ramified supercuspidal representations of Gln ’, Pacific J. Math. 73(2) (1977), 437–460.Google Scholar
Kaletha, T., Minguez, A., Shin, S. W. and White, P.-J., ‘Endoscopic classification of representations: Inner forms of unitary groups’, Preprint, 2014, arXiv:1409.3731.Google Scholar
Knapp, A. W., Representation Theory of Semisimple Groups, Princeton Landmarks in Mathematics , (Princeton University Press, Princeton, NJ, 2001).Google Scholar
Lapid, E., ‘On the support of matrix coefficients of supercuspidal representations of the general linear group over a local non-archimedean field’, Preprint, 2018,arXiv:1802.07154.Google Scholar
Marshall, S., ‘Endoscopy and cohomology growth on U (3)’, Compos. Math. 150(6) (2014), 903–910.Google Scholar
Marshall, S., ‘Endoscopy and cohomology growth on a quasi-split U (4)’, inFamilies of Automorphic Forms and the Trace Formula, Simons Symposia (Springer International Publishing Switzerland, 2016), 297–325.Google Scholar
Meyer, R. and Solleveld, M., ‘Characters and growth of admissible representations of reductive p-adic groups’, J. Inst. Math. Jussieu 11(2) (2012), 289–331.Google Scholar
Moeglin, C. and Renard, D., ‘Sur les paquets d’Arthur aux places réels, translation’, inGeometric Aspects of the Trace Formula, Simons Symposia (Springer International Publishing, Switzerland, 2018), 299–320.Google Scholar
Moeglin, C. and Waldspurger, J.-L., Stabilisation de la formule des traces tordue, Vol. 1, Progress in Mathematics, 316 (Birkhäuser/Springer, Cham, 2016).Google Scholar
Moeglin, C. and Waldspurger, J.-L., Stabilisation de la formule des traces tordue, Vol. 2, Progress in Mathematics, 317 (Birkhäuser/Springer, Cham, 2016).Google Scholar
Mok, C. P., ‘Endoscopic classification of representations of quasi-split unitary groups’, Mem. Amer. Math. Soc. 235(1108) (2015), vi+248.Google Scholar
Moy, A., ‘Local constants and the tame Langlands correspondence’, Amer. J. Math. 108(4) (1986), 863–930.Google Scholar
Rogawski, J. D., ‘Analytic expression for the number of points mod p ’, inThe Zeta Functions of Picard Modular Surfaces (Univ. Montréal, Montreal, QC, 1992), 65–109.Google Scholar
Sarnak, P. and Xue, X. X., ‘Bounds for multiplicities of automorphic representations’, Duke Math. J. 64(1) (1991), 207–227.Google Scholar
Savin, G., ‘Limit multiplicities of cusp forms’, Invent. Math. 95(1) (1989), 149–159.Google Scholar
Vogan, D. A. Jr., ‘Unitarizability of certain series of representations’, Ann. of Math. (2) 120(1) (1984), 141–187.Google Scholar
Vogan, D. A. Jr. and Zuckerman, G. J., ‘Unitary representations with nonzero cohomology’, Compos. Math. 53(1) (1984), 51–90.Google Scholar
Wallach, N. R., ‘On the constant term of a square integrable automorphic form’, inOperator Algebras and Group Representations, Vol. II (Neptun, 1980), Monographs and Studies in Mathematics, 18 (Pitman, Boston, MA, 1984), 227–237.Google Scholar
Xue, X. X., ‘On the first Betti numbers of hyperbolic surfaces’, Duke Math. J. 64(1) (1991), 85–110.Google Scholar