Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
Hostname: page-component-559fc8cf4f-67gxp Total loading time: 0.268 Render date: 2021-03-07T06:03:46.858Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false, "newCitedByModal": true }
EnglishFrançais
Forum of Mathematics, Sigma Forum of Mathematics, Sigma

Article contents

GL-EQUIVARIANT MODULES OVER POLYNOMIAL RINGS IN INFINITELY MANY VARIABLES. II

Published online by Cambridge University Press:  12 March 2019

STEVEN V SAM  and
ANDREW SNOWDEN
STEVEN V SAM
Affiliation:
Department of Mathematics, University of California, San Diego, CA, USA; ssam@ucsd.edu; http://math.ucsd.edu/∼ssam/
ANDREW SNOWDEN
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI, USA; asnowden@umich.edu; http://www-personal.umich.edu/∼asnowden/
Corresponding
E-mail address:
ssam@ucsd.edu
asnowden@umich.edu
Save pdf (0.45 mb)

Abstract

Twisted commutative algebras (tca’s) have played an important role in the nascent field of representation stability. Let 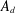$A_{d}$ be the tca freely generated by 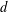$d$ indeterminates of degree 1. In a previous paper, we determined the structure of the category of 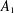$A_{1}$ -modules (which is equivalent to the category of 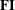$\mathbf{FI}$ -modules). In this paper, we establish analogous results for the category of 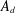$A_{d}$ -modules, for any 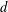$d$ . Modules over 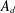$A_{d}$ are closely related to the structures used by the authors in previous works studying syzygies of Segre and Veronese embeddings, and we hope the results of this paper will eventually lead to improvements on those works. Our results also have implications in asymptotic commutative algebra.

Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e5
Creative Commons
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike licence (http://creativecommons.org/licenses/by-nc-sa/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the same Creative Commons licence is included and the original work is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use.
Copyright
© The Author(s) 2019

References

Akin, K. and Weyman, J., ‘Minimal free resolutions of determinantal ideals and irreducible representations of the Lie superalgebra gl (m|n)’, J. Algebra 197(2) (1997), 559–583.CrossRefGoogle Scholar
Assmus, E. F. Jr, ‘On the homology of local rings’, Illinois J. Math. 3 (1959), 187–199.Google Scholar
Church, T. and Ellenberg, J. S., ‘Homological properties of FI-modules and stability’, Geom. Topol. to appear, arXiv:1506.01022v2.Google Scholar
Church, T., Ellenberg, J. S. and Farb, B., ‘FI-modules and stability for representations of symmetric groups’, Duke Math. J. 164(9) (2015), 1833–1910.CrossRefGoogle Scholar
Church, T. and Farb, B., ‘Representation theory and homological stability’, Adv. Math. (2013), 250–314. arXiv:1008.1368v3.CrossRefGoogle Scholar
Dade, E. C., ‘Localization of injective modules’, J. Algebra 69(2) (1981), 416–425.CrossRefGoogle Scholar
de Concini, C., Eisenbud, David and Procesi, C., ‘Young diagrams and determinantal varieties’, Invent. Math. 56(2) (1980), 129–165.CrossRefGoogle Scholar
Gabriel, P., ‘Des catégories abéliennes’, Bull. Soc. Math. France 90 (1962), 323–448.CrossRefGoogle Scholar
Hartshorne, R., Residues and Duality, Lecture Notes in Mathematics, 20 (Springer, Berlin–New York, 1966).CrossRefGoogle Scholar
Jantzen, J. C., Representations of Algebraic Groups, Pure and Applied Mathematics, 131 , (Academic Press, Boston, MA, 1987).Google Scholar
Kapranov, M. M., ‘On the derived categories of coherent sheaves on some homogeneous spaces’, Invent. Math. 92(3) (1988), 479–508.CrossRefGoogle Scholar
Nagpal, R., Sam, S. V. and Snowden, A., ‘Noetherianity of some degree two twisted commutative algebras’, Selecta Math. (N.S.) 22(2) (2016), 913–937.CrossRefGoogle Scholar
Raicu, C., ‘Regularity and cohomology of determinantal thickenings’, arXiv:1611.00415v1.Google Scholar
Ramos, Eric, ‘Generalized representation stability and FI d -modules’, Proc. Amer. Math. Soc. (2016), to appear, arXiv:1606.02673v4.Google Scholar
Ramos, E., ‘Configuration spaces of graphs with certain permitted collisions’, arXiv:1703.05535v1.Google Scholar
Raicu, C. and Weyman, J., ‘Local cohomology with support in generic determinantal ideals’, Algebra Number Theory 8(5) (2014), 1231–1257.CrossRefGoogle Scholar
Raicu, C. and Weyman, J., ‘The syzygies of some thickenings of determinantal varieties’, Proc. Amer. Math. Soc. 145(1) (2017), 49–59.CrossRefGoogle Scholar
Steven, V Sam, ‘Ideals of bounded rank symmetric tensors are generated in bounded degree’, Invent. Math. 207(1) (2017), 1–21.Google Scholar
Sam, S. V., ‘Syzygies of bounded rank symmetric tensors are generated in bounded degree’, Math. Ann. 368(3) (2017), 1095–1108.CrossRefGoogle Scholar
Steven, V Sam and Snowden, Andrew, ‘GL-equivariant modules over polynomial rings in infinitely many variables’, Trans. Amer. Math. Soc. 368 (2016), 1097–1158.Google Scholar
Sam, S. V. and Snowden, A., ‘Introduction to twisted commutative algebras’, arXiv:1209.5122v1.Google Scholar
Sam, S. V. and Snowden, A., ‘Gröbner methods for representations of combinatorial categories’, J. Amer. Math. Soc. 30 (2017), 159–203.CrossRefGoogle Scholar
Sam, S. V. and Snowden, A., ‘Hilbert series for twisted commutative algebras’, Algebraic Combin. 1(1) (2018), 147–172.CrossRefGoogle Scholar
Sam, S. V. and Snowden, A., Depth and local cohomology of twisted commutative algebras; in preparation.Google Scholar
Sam, S. V. and Snowden, A., ‘Regularity bounds for twisted commutative algebras’, arXiv:1704.01630v1.Google Scholar
Snowden, Andrew, ‘Syzygies of Segre embeddings and 𝛥-modules’, Duke Math. J. 162(2) (2013), 225–277.CrossRefGoogle Scholar
Stacks Project, http://stacks.math.columbia.edu, 2017.Google Scholar
Weyman, J., Cohomology of Vector Bundles and Syzygies 149 (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar

Altmetric attention score

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 200 *
View data table for this chart

* Views captured on Cambridge Core between 12th March 2019 - 7th March 2021. This data will be updated every 24 hours.

Access
Open access
3 Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

GL-EQUIVARIANT MODULES OVER POLYNOMIAL RINGS IN INFINITELY MANY VARIABLES. II
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

GL-EQUIVARIANT MODULES OVER POLYNOMIAL RINGS IN INFINITELY MANY VARIABLES. II
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

GL-EQUIVARIANT MODULES OVER POLYNOMIAL RINGS IN INFINITELY MANY VARIABLES. II
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *