No CrossRef data available.
Article contents
A PROOF OF ANDREWS’ CONJECTURE ON PARTITIONS WITH NO SHORT SEQUENCES
Published online by Cambridge University Press: 30 May 2019
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Our main result establishes Andrews’ conjecture for the asymptotic of the generating function for the number of integer partitions of 
$n$ without 
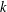$k$ consecutive parts. The methods we develop are applicable in obtaining asymptotics for stochastic processes that avoid patterns; as a result they yield asymptotics for the number of partitions that avoid patterns.
Holroyd, Liggett, and Romik, in connection with certain bootstrap percolation models, introduced the study of partitions without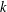 
$k$ consecutive parts. Andrews showed that when 
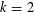$k=2$, the generating function for these partitions is a mixed-mock modular form and, thus, has modularity properties which can be utilized in the study of this generating function. For 
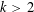$k>2$, the asymptotic properties of the generating functions have proved more difficult to obtain. Using 
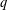$q$-series identities and the 
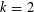$k=2$ case as evidence, Andrews stated a conjecture for the asymptotic behavior. Extensive computational evidence for the conjecture in the case 
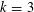$k=3$ was given by Zagier.
This paper improved upon early approaches to this problem by identifying and overcoming two sources of error. Since the writing of this paper, a more precise asymptotic result was established by Bringmann, Kane, Parry, and Rhoades. That approach uses very different methods.
MSC classification
- Type
- Research Article
- Information
- Creative Commons
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.- Copyright
- © The Author(s) 2019
References
Aizenman, M. and Lebowitz, J., ‘Metastability effects in bootstrap percolation’, J. Phys. (A)
21 (1988), 3801–3813.Google Scholar
Andrews, G. E., ‘Partitions with short sequences and mock theta functions’, Proc. Natl. Acad. Sci. USA
102 (2005), 4666–4671.Google Scholar
Andrews, G. E., Eriksson, H., Petrov, F. and Romik, D., ‘Integrals, partitions and MacMahon’s theorem’, J. Combin. Theory (A)
114 (2007), 545–555.Google Scholar
Andrews, G. E. and Lewis, R. P., ‘An algebraic identity of F. H. Jackson and its implications for partitions’, Discrete Math.
232 (2001), 77–83.Google Scholar
Baxter, R. J., Exactly Solved Models in Statistical Mechanics, (Academic Press, London and New York, 1982).Google Scholar
Bringmann, K., Kane, B., Parry, D. and Rhoades, R. C., ‘On the Andrews–Zagier asymptotics for partitions without sequences’, Adv. Math.
309 (2017), 436–451.Google Scholar
Bringmann, K. and Mahlburg, K., ‘An extension of the Hardy–Ramanujan Circle Method and applications to partitions without sequences’, Amer. J. Math.
133 (2011), 1151–1178.Google Scholar
Bringmann, K. and Mahlburg, K., ‘Improved bounds on metastability thresholds and probabilities for generalized bootstrap percolation’, Trans. Amer. Math. Soc.
364 (2012), 3829–3859.Google Scholar
Bringmann, K., Mahlburg, K. and Mellit, A., ‘Convolution bootstrap percolation models, Markov-type stochastic processes, and mock theta functions’, Int. Math. Res. Not. (2013), 971–1013.Google Scholar
Bringmann, K., Mahlburg, K. and Nataraj, K., ‘Distinct parts partitions without sequences’, Electronic J. Combin.
22 (2015), Paper 3.3, 13 pp.Google Scholar
Bringmann, K., Holroyd, A., Mahlburg, K. and Vlasenko, M., ‘
k-run overpartitions and mock theta functions’, Q. J. Math.
64 (2013), 1009–1021.Google Scholar
Fristedt, B., ‘The structure of random partitions of large integers’, Trans. Amer. Math. Soc.
337(2) 703–735.Google Scholar
Gravner, J. and Holroyd, A., ‘Slow convergence in bootstrap percolation’, Ann. Appl. Probab.
18 (2008), 909–928.Google Scholar
Griffiths, D. J., Introduction to Quantum Mechanics, second edition, (Pearson Education Inc., Upper Saddle River NJ, 2005).Google Scholar
Holroyd, A. E., ‘Sharp metastability threshold for two-dimensional bootstrap percolation’, Probab. Theory Related Fields
125 (2003), 195–224.Google Scholar
Holroyd, A. E., Liggett, T. M. and Romik, D., ‘Integrals, partitions, and cellular automata’, Trans. Amer. Math Soc.
356 (2004), 3349–3368.Google Scholar
Ingham, A., ‘A Tauberian theorem for partitions’, Ann. of Math. (2)
42 (1941), 1075–1090.Google Scholar
Knopfmacher, A. and Munagi, A. O., ‘Successions in integer partitions’, Ramanujan J.
18 (2009), 239–255.Google Scholar
MacMahon, P. A., Combinatorial Analysis, Vol. 2, (Cambridge University Press, New York, 1916), Reprinted Dover.Google Scholar
Ono, K., ‘Unearthing the visions of a master: harmonic Maass forms and number theory’, inCurrent Developments in Mathematics (Int. Press, Somerville, MA, 2009), 347–454.Google Scholar
Zagier, D., ‘Ramanujan’s mock theta functions and their applications [d’aprés Zwegers and Bringmann-Ono]’, inSém. Bourbaki (2007/2008), Astérisque, No. 326, Exp. No. 986, vii–viii (2010), 143–164.Google Scholar
Zagier, D., private communication.Google Scholar
Zwegers, S., ‘Mock theta functions’, PhD Thesis (Advisor: D. Zagier), Universiteit Utrecht, (2002).Google Scholar
You have
Access
Open access