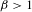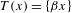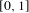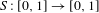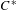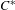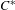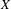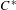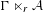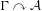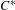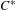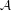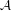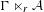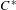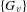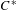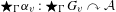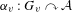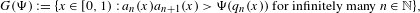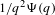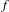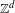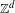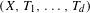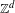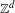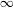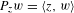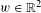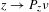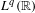Original Article
Generic point equivalence and Pisot numbers
- Part of:
-
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3169-3180
-
- Article
- Export citation
On simplicity of intermediate
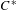 $C^{\ast }$-algebras
$C^{\ast }$-algebras
- Part of:
-
- Published online by Cambridge University Press:
- 06 June 2019, pp. 3181-3187
-
- Article
- Export citation
On graph products of multipliers and the Haagerup property for
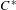 $C^{\ast }$-dynamical systems
$C^{\ast }$-dynamical systems
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2019, pp. 3188-3216
-
- Article
- Export citation
The sets of Dirichlet non-improvable numbers versus well-approximable numbers
- Part of:
-
- Published online by Cambridge University Press:
- 27 June 2019, pp. 3217-3235
-
- Article
- Export citation
Fast and slow points of Birkhoff sums
- Part of:
-
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3236-3256
-
- Article
- Export citation
Directional dynamical cubes for minimal
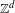 $\mathbb{Z}^{d}$-systems
$\mathbb{Z}^{d}$-systems
- Part of:
-
- Published online by Cambridge University Press:
- 26 June 2019, pp. 3257-3295
-
- Article
- Export citation
Refined scales of weak-mixing dynamical systems: typical behaviour
- Part of:
-
- Published online by Cambridge University Press:
- 26 June 2019, pp. 3296-3309
-
- Article
- Export citation
On the geodesic flow on CAT(0) spaces
- Part of:
-
- Published online by Cambridge University Press:
- 15 August 2019, pp. 3310-3338
-
- Article
- Export citation
Global fixed points for nilpotent actions on the torus
- Part of:
-
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3339-3367
-
- Article
- Export citation
Variations around Eagleson’s theorem on mixing limit theorems for dynamical systems
- Part of:
-
- Published online by Cambridge University Press:
- 26 June 2019, pp. 3368-3374
-
- Article
- Export citation
Finite-dimensional approximations for Nica–Pimsner algebras
- Part of:
-
- Published online by Cambridge University Press:
- 09 August 2019, pp. 3375-3402
-
- Article
- Export citation
Quasi-Sturmian colorings on regular trees
- Part of:
-
- Published online by Cambridge University Press:
- 09 August 2019, pp. 3403-3419
-
- Article
- Export citation
Null systems in the non-minimal case
- Part of:
-
- Published online by Cambridge University Press:
- 17 June 2019, pp. 3420-3437
-
- Article
- Export citation
On self-similar measures with absolutely continuous projections and dimension conservation in each direction
- Part of:
-
- Published online by Cambridge University Press:
- 26 June 2019, pp. 3438-3456
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 40 Issue 12 Cover and Front matter
-
- Published online by Cambridge University Press:
- 02 November 2020, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 40 Issue 12 Cover and Back matter
-
- Published online by Cambridge University Press:
- 02 November 2020, pp. b1-b2
-
- Article
-
- You have access
- Export citation