No CrossRef data available.
Article contents
Generic point equivalence and Pisot numbers
Part of:
Probabilistic theory: distribution modulo $1$; metric theory of algorithms
Low-dimensional dynamical systems
Published online by Cambridge University Press: 11 July 2019
Abstract
Let  $\unicode[STIX]{x1D6FD}>1$ be an integer or, generally, a Pisot number. Put
$\unicode[STIX]{x1D6FD}>1$ be an integer or, generally, a Pisot number. Put 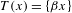 $T(x)=\{\unicode[STIX]{x1D6FD}x\}$ on
$T(x)=\{\unicode[STIX]{x1D6FD}x\}$ on 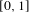 $[0,1]$ and let
$[0,1]$ and let 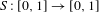 $S:[0,1]\rightarrow [0,1]$ be a piecewise linear transformation whose slopes have the form
$S:[0,1]\rightarrow [0,1]$ be a piecewise linear transformation whose slopes have the form 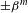 $\pm \unicode[STIX]{x1D6FD}^{m}$ with positive integers
$\pm \unicode[STIX]{x1D6FD}^{m}$ with positive integers  $m$. We give a sufficient condition for
$m$. We give a sufficient condition for  $T$ and
$T$ and  $S$ to have the same generic points. We also give an uncountable family of maps which share the same set of generic points.
$S$ to have the same generic points. We also give an uncountable family of maps which share the same set of generic points.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2019
References
Airey, D., Jackson, S., Kwietniak, D. and Mance, B.. Borel complexity of sets of normal numbers via generic points in subshifts with specification. Preprint, 2018, arXiv:1811.04450v1.Google Scholar
Bertrand-Mathis, A.. Développement en base 𝜃; répartition modulo un de la suite (x𝜃n)n≥0 ; langages codés et 𝜃-shift. Bull. Soc. Math. France 114 (1986), 271–323.Google Scholar
Garsia, A. M.. Arithmetic properties of Bernoulli convolutions. Trans. Amer. Math. Soc. 102 (1962), 409–432.Google Scholar
Góra, P.. Invariant densities for generalized 𝛽-maps. Ergod. Th. & Dynam. Sys. 27(5) (2007), 1583–1598.Google Scholar
Góra, P.. Invariant densities for piecewise linear maps of the unit interval. Ergod. Th. & Dynam. Sys. 29(5) (2009), 1549–1583.Google Scholar
Handelman, D.. Spectral radii of primitive integral companion matrices and log concave polynomials. Symbolic Dynamics and its Applications (New Haven, CT, 1991) (Contemporary Mathematics, 135). American Mathematical Society, Providence, RI, 1992, pp. 231–237.Google Scholar
Ito, S. and Takahashi, Y.. Markov subshifts and realization of 𝛽-expansions. J. Math. Soc. Japan 26(1) (1974), 33–55.Google Scholar
Jäger, H.. On decimal expansions. Zahlentheorie (Tagung), Math. Forschungsinst. Oberwolfach, 1970 (Bereich Math. Forschungsinst., Oberwolfach, Heft 5). Bibliographisches Institut, Mannheim, 1971, pp. 67–75.Google Scholar
Jung, S. and Volkmann, B.. Remarks on a paper of Wagner. J. Number Theory 56(2) (1996), 329–335.Google Scholar
Kano, H. and Shiokawa, I.. Rings of normal and nonnormal numbers. Israel J. Math. 84(3) (1993), 403–416.Google Scholar
Ki, H. and Linton, T.. Normal numbers and subset of N with given densities. Fund. Math. 144(2) (1994), 163–179.Google Scholar
Kopf, C.. Invariant measures for piecewise linear transformations of the interval. Appl. Math. Comput. 39(2) (1990), 123–144, part II.Google Scholar
Kowalski, Z.. Invariant measure for piecewise monotonic transformation has a positive lower bound on its support. Bull. Acad. Polon. Sci. Ser. Sci. Math. 27(1) (1979), 53–57.Google Scholar
Kraaikamp, C. and Nakada, H.. On a problem of Schweiger concerning normal numbers. J. Number Theory 86 (2001), 330–340.Google Scholar
Li, T. Y. and Yorke, J. A.. Ergodic transformations from an interval into itself. Trans. Amer. Math. Soc. 235 (1978), 183–192.Google Scholar
Moshchevitin, N. G. and Shkredov, I. D.. On the Pyatetskii–Shapiro criterion of normality. Math. Notes 73 (2003), 539–550.Google Scholar
Parry, W.. On the 𝛽-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.Google Scholar
Parry, W.. Representations for real numbers. Acta Math. Acad. Sci. Hungar. 15 (1964), 95–105.Google Scholar
Pollington, A. D.. The Hausdorff dimension of a set of normal numbers. Pacific J. Math. 95 (1981), 193–204.Google Scholar
Postnikov, A. G.. Ergodic problems in the theory of congruences and of diophantine approximations. Trudy Mat. Inst. Steklov 82 (1966), 3–112 (in Russian); Engl. trans. Proc. Steklov Inst. Math. 82 (1966), 1–128.Google Scholar
Schweiger, F.. Normalität bezüglich zahlentheoretischer Transformationen. J. Number Theory 1 (1969), 390–397.Google Scholar
Sharkovsky, A. N. and Sivak, A. G.. Basin of attractors of trajectories. J. Difference Equ. Appl. 22(2) (2016), 159–163.Google Scholar
Vandehey, J.. On the joint normality of certain digit expansions. Preprint, 2014, arXiv:1408.0435.Google Scholar
Wagner, G.. On rings of numbers which are normal to one base but non-normal to another. J. Number Theory 54(2) (1995), 211–231.Google Scholar
Wall, D. D.. Normal numbers. PhD Thesis, University of California, Berkeley, 1949.Google Scholar





